Jerarquía de las operaciones I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Jerarquía de las operaciones I
Aprendizaje esperado: determina y usa la jerarquía de operaciones y los paréntesis en operaciones con números naturales, enteros y decimales (para multiplicación y división, sólo números positivos).
Énfasis: resolver oraciones numéricas empleando la jerarquía de las operaciones con números naturales, enteros y decimales.
¿Qué vamos a aprender?
En esta sesión resolverás operaciones numéricas empleando la jerarquía de operaciones con números naturales, enteros y decimales.
¿Qué hacemos?
En la solución de enunciados matemáticos es posible utilizar calculadora. Sin embargo, es necesario que antes sepas cómo resolver las operaciones sin la ayuda de esta herramienta. Por ejemplo, usar una calculadora para verificar un resultado puede ser de utilidad.
¿En qué circunstancias más puede ayudarte el uso de una calculadora?
Puede ayudar a hacer una gran cantidad de operaciones en menor tiempo. Claro, cuando ya sabes cómo hacer dichos cálculos, y has comprendido los procedimientos, se puede usar para facilitarte su resolución.
Por ejemplo, cuando hay que resolver enunciados matemáticos en los que debes considerar la jerarquía de operaciones, antes de usar la calculadora, es necesario comprender el orden en el que se deben hacer dichas operaciones. Aunque hay calculadoras programadas para considerar la jerarquía de operaciones, no todas lo están. De ahí la importancia de conocer y comprender el orden de ejecución correcto para resolverlas.
¿Qué te parece si verificas cuál es la correcta jerarquía de operaciones?
Pon atención a la explicación, en el siguiente video.
- “Jerarquía de operaciones”.
Jerarquía de operaciones: Jerarquía es un orden, en este caso, el orden en que deberás resolver las operaciones de un enunciado numérico. Existe un orden de ejecución específico.
En el primer nivel del orden de ejecución están las operaciones agrupadas, a través de los paréntesis, los corchetes y las llaves. Cuando en un enunciado matemático aparecen estos signos de agrupación las operaciones contenidas deben ser las primeras en resolverse.
En el segundo nivel del orden de ejecución, se operan los exponentes y raíces, por ahora no se usarán, lo harás más adelante. Sin embargo, se menciona para que conozcas todos los niveles de la jerarquía de operaciones.
En el tercer nivel del orden de ejecución están las multiplicaciones y divisiones. Nota que están juntas y, por consiguiente, tienen la misma jerarquía: multiplicaciones y divisiones.
En el cuarto y último nivel del orden de ejecución, se encuentran las sumas y las restas. Esto significa que son las últimas operaciones que se realizan, y están en el mismo nivel de jerarquía.
Cabe señalar que cuando en un enunciado numérico sólo hay operaciones de la misma jerarquía, es decir, que se encuentran en el mismo nivel de ejecución, simplemente se realizan de izquierda a derecha.
Con esta información, es posible resolver diferentes enunciados matemáticos y luego verificar los resultados con la calculadora.
A lo largo de esta sesión resolverás diferentes operaciones combinadas o enunciados matemáticos, usando la jerarquía de operaciones. De manera que, si tienes disponible una calculadora, podrás verificar los resultados en ella.
Se comenzará con el primer enunciado matemático.
4.5 por 2 menos 8 más 18 entre 3.
El primer nivel del orden de ejecución según la jerarquía de operaciones, son las operaciones agrupadas. Nota que en este enunciado matemático no hay signos de agrupación, por consiguiente, se avanza al siguiente nivel de ejecución, que son los exponentes y las raíces, que tampoco existen en el enunciado.
Lo que sí aparece, es una multiplicación y una división, se resaltan estas dos operaciones para que puedas observarlas mejor. Hay que considerar que las multiplicaciones y divisiones se encuentran en el tercer nivel de ejecución, por lo tanto, tienen la misma jerarquía.
Así que, para este enunciado, estas son las operaciones que se deben realizar primero. Se comienza de izquierda a derecha.
Primero, se resuelve la multiplicación 4.5 por 2 que da como resultado 9. Enseguida, hay que enfocarse en la división 18 entre 3 que da como resultado 6. Ahora puedes reescribir el enunciado matemático equivalente como 9 menos 8 más 6. Éstas son sumas y restas que se encuentran en el cuarto nivel del orden de ejecución y como tienen la misma jerarquía se resuelven de izquierda a derecha. Así: 9 menos 8 igual a 1 y 1 más 6 igual a 7. Por lo que el resultado final es 7.

Explicado de esa manera te puede resultar más claro.
Puedes validar estos resultados usando tu calculadora, si la tienes disponible.
Busca retroalimentación si te es posible de tu maestra o maestro con respecto a los resultados que obtengas.
¿Cómo resolverías un enunciado en el que aparezcan signos de agrupación?
Ahora, se resolverá otro ejemplo, pero que tenga paréntesis. Algo importante a tener en consideración, es que las operaciones agrupadas, pueden estar contenidas en múltiples signos de agrupación, conforme hay necesidad de hacer más agrupaciones se recurre, en primera instancia, a los paréntesis, luego a los corchetes y después a las llaves. En ocasiones, sobre todo en programación informática la agrupación solamente se realiza con paréntesis lo que requiere mucha observación para abrir y cerrar agrupaciones de forma correcta.
Sea el enunciado matemático:
50 menos, se abre paréntesis, 9 por 3 más 13, se cierra paréntesis, más cinco menos, se abre paréntesis, ocho más cuatro por 2, se cierra paréntesis.
En primer orden de ejecución, se encuentran las operaciones agrupadas. En este enunciado hay dos agrupaciones con paréntesis, que se resaltan para que puedas identificarlas mejor.
Ahora, se procederá a resolver las operaciones contenidas en cada agrupación. Se comienza con, 9 por 3 más 13. Por jerarquía de operaciones, primero se realiza la multiplicación quedando 9 por 3 igual a 27. Luego, la suma: 27 más 13 igual a 40. Así que el resultado de la primera agrupación es 40.
Enseguida, se procede a resolver las operaciones de la segunda agrupación, 8 más 4 por 2. De igual manera, por jerarquía de operaciones, primero se resuelve la multiplicación 4 por 2 igual a 8. Luego, se opera la suma 8 más 8 que resulta 16.
En este momento, ya es posible reescribir el enunciado matemático equivalente:
50 menos 40 más 5 menos 16. Como son sumas y restas y están en el mismo nivel de ejecución se resuelve de izquierda a derecha:
50 menos 40 igual a 10.
10 más 5 igual a 15.
15 menos 16 igual a 1 negativo.

La jerarquía de operaciones también se usa de la misma forma para las operaciones dentro de los paréntesis. Puedes usar tu calculadora para verificar los resultados. Pero, ¿cómo se introducen los paréntesis en la calculadora?
Busca orientación de tu maestra o maestro para hacerlo si no conoces la manera, ¿cómo resolverías un enunciado en el que aparezcan además de paréntesis, llaves y corchetes?
Ahora, se resolverá un ejemplo en donde se involucran estos signos de agrupación, para responder la pregunta que se plantea. No olvides que, cuando realizas las operaciones, conforme a la jerarquía que ya conoces, los paréntesis, corchetes y llaves, determinan el orden y la prioridad de unas sobre otras.
Algunas consideraciones importantes para resolver las operaciones contenidas en los signos de agrupación son:
Primero.
Cuando existen signos de agrupación contiguos, se traduce como el producto de ambas agrupaciones.
Por ejemplo:
(20 - 5 x 3) (9 - 2 x 4)
(20-15) (9 - 8)
(5) (1)
5
Segundo.
Cuando un número precede a un signo de agrupación, significa que ese número multiplica al contenido de la agrupación.
Por ejemplo:
3.5 (2 + 3 x 3)
3.5 (2 + 9)
3.5 (11)
38.5
Tercero.
Por lo general, es conveniente comenzar resolviendo las operaciones que se encuentren contenidas dentro de paréntesis. Estas operaciones suelen estar en la parte central de la misma. Enseguida, las operaciones entre corchetes y, finalmente, las que están contenidas entre llaves.
Por ejemplo:
2 {(16 – 4 x 2 ) + [ 3 – (4 ÷ 2 – 1) ] + 4 (2 + 3 x 2)}
2{(16 – 8) + [3 - ( 2 – 1) ] + 4 (2 + 6)}
2{8 + [ 3 - ( 1) ] + 4 (8)}
2{8 + [ 3 – 1] + 32}
2{8 + 2 + 32}
2{42}
84
Con estas orientaciones podrás resolver un enunciado matemático semejante al que se ha resuelto.
Ahora escribe en tu cuaderno el enunciado y trata de resolverlo.
El enunciado es: Dos, se abre llave, cuatro, se abre corchete, cinco, menos, se abre paréntesis, dos por uno, se cierra paréntesis, se cierra corchete y se cierra llave.
Como tienes varios signos de agrupación debes comenzar con los paréntesis; es decir, dos por uno, que es igual a dos, con esto, ya eliminas los paréntesis, porque al paréntesis lo antecede un signo menos, quedando: dos, se abre llave, cuatro, se abre corchete, cinco, menos dos se cierra corchete y se cierra llave.
La siguiente operación que debes realizar es la que se encuentra dentro del corchete; es decir, cinco menos dos, que es igual a tres. Antes del corchete se encuentra un número, el cual multiplica al tres; por ello, se conserva el corchete. Entonces se resuelve cuatro por tres es igual a doce. Por lo tanto, queda: dos, se abre llave, doce, se cierra llave. Por último, como antes de la llave no hay signos de menos ni de más, se debe multiplicar al doce por dos. Así sabes que la respuesta a este enunciado matemático es 2 por 12 igual a veinticuatro.

En casa ¿obtuviste el mismo resultado?
Si no fue así, comenta con tu maestra o maestro para recibir retroalimentación.
Ahora hay que verificarlo en la calculadora.
Si tienes a la mano una calculadora resuélvelo a la par que se hace aquí, si no tienes realiza el procedimiento en tu cuaderno.
Tal vez te pueda suceder lo siguiente: que tu calculadora no tiene corchetes, ni llaves, y solo veas una tecla con un paréntesis que abre y otra con un paréntesis que cierra. En este caso, ¿qué debes hacer para colocar los corchetes y las llaves?
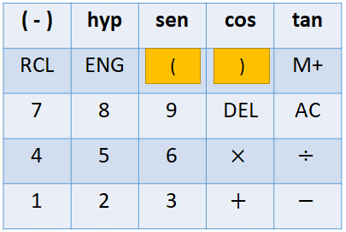
En algunas ocasiones puedes encontrar enunciados numéricos en los que se observa solamente paréntesis, y la forma en que se debe operar con ellos es exactamente igual: siempre partiendo del centro hacia afuera.
Por eso, en algunas calculadoras no encontrarás los corchetes ni las llaves; sin problema alguno, puedes utilizar sólo los paréntesis, siempre y cuando tengas cuidado de que estén en pareja, es decir por cada paréntesis que se abra, debe haber uno que cierre.
Con lo que se acaba de explicar, el enunciado numérico queda de la siguiente manera: dos, se abre paréntesis, cuatro, se abre paréntesis, cinco, menos, se abre paréntesis, dos por uno, se cierra paréntesis, se cierra paréntesis y se cierra paréntesis.

Así como se describe arriba, es el orden de las teclas que debes oprimir en la calculadora. Seguido del signo igual.
Si realizas el ejercicio en la calculadora podrás verificar que el resultado es 24. ¡Por lo tanto, es correcto!
Ahora hay que ver el procedimiento, para el caso, de que no cuentes con calculadora y verifiques si lo hiciste de forma correcta.
Se comenzará con la operación del paréntesis que se encuentra en el centro, realizas la operación dos por uno, lo que resulta dos. Antes de este paréntesis se encuentra un signo de menos, por lo tanto, para poder eliminar dicho paréntesis debes escribir el dos, precedido del signo negativo; de esta manera se obtiene: dos, se abre paréntesis, cuatro, se abre paréntesis, cinco menos dos, se cierra paréntesis y se cierra paréntesis.
Se vuelve a operar con el paréntesis que se encuentra en el centro. En este caso es una resta: cinco menos dos, que resulta tres. Para eliminar el paréntesis en el que se encuentra el tres, debes multiplicar por el número que lo antecede; es decir, por cuatro, de lo cual se obtiene doce. Quedando dos, se abre paréntesis, doce, se cierra paréntesis.
Para eliminar el último paréntesis, multiplicas dos por doce lo que resulta veinticuatro.

Como viste se obtuvo el mismo resultado.
Ahora se revisará una situación más en la que sea relevante la jerarquía de operaciones.
En las ciencias, en diversas situaciones de la vida cotidiana o en algunas empresas, se hace necesario convertir las mediciones de temperatura de grados Fahrenheit a grados Celsius. Por ejemplo, en países como Estados Unidos se mide la temperatura en grados Fahrenheit.
Ahora, se explicará cómo se hace para encontrar el equivalente a grados Celsius.
Para convertir el valor de una temperatura dada en grados Fahrenheit a grados Celsius, primeramente, se resta 32 al valor de la temperatura en grados Fahrenheit; enseguida, se multiplica por 5 y, finalmente, se divide entre 9.
Conforme a la jerarquía de operaciones, si deseas convertir 95 grados Fahrenheit a grados Celsius, ¿cuál de las siguientes dos opciones corresponde a la forma de conversión que se explicó?
Primera opción:
95 menos, se abre paréntesis, 32 por 5, se cierra paréntesis, entre 9.
Segunda opción:
Se abre corchete, se abre paréntesis, 95 menos 32, se cierra paréntesis, por 5, se cierra corchete, entre 9.

En este caso ¿consideras que primero se resuelve la operación del paréntesis y luego la del corchete?
¡Así es! Generalmente el orden es paréntesis, corchete y luego llave.
Entonces la segunda opción es la respuesta correcta. ¿Qué opinas?
¡Es correcto! Resuelve las operaciones para obtener la equivalencia correspondiente.
Antes de terminar, se planteará un último ejercicio. Las fórmulas geométricas son expresiones que permiten generalizar, por ejemplo, sabes que el área de un rectángulo se obtiene multiplicando la medida de la base por la altura, lo cual se representa como A igual a b por h. Donde b representa la base y h la altura.
Así, el área de un trapecio es igual a la suma de las bases por la altura entre 2.
Si B mayúscula representa la base mayor, b minúscula la base menor y h la altura, ¿cómo representarías algebraicamente el área, aplicando adecuadamente la jerarquía de las operaciones. Analiza las siguientes opciones:
Primera opción: área es igual a, h sobre 2 por b mayúscula más b minúscula.
Segunda opción: h, se abre paréntesis, b mayúscula más b minúscula, se cierra paréntesis, todo entre 2.

¿Qué opción muestra la representación adecuada?
La fórmula indica que se tienen que sumar las bases, y posteriormente, multiplicar por la altura y dividir entre 2, por ello, la opción 1 no es correcta, porque no se usan correctamente los paréntesis para priorizar la suma y en este caso, primero se tiene que multiplicar por b mayúscula y posteriormente sumar b minúscula.
En la segunda opción, se usan paréntesis para priorizar la suma de b más b, y como la propiedad conmutativa de la multiplicación indica que el orden de los factores no altera el producto, entonces está opción es correcta.
Así es, una manera equivalente de representar esta misma fórmula es: Se abre paréntesis, b mayúscula por b minúscula, se cierra paréntesis, por h entre 2. En casa, ¿se te ocurre otra manera? Reflexiónalo y da repuesta en casa.
Has concluido el tema del día de hoy. Si quieres conocer más sobre este tema puedes consultar tu libro de texto o bien también puedes pedir apoyo, y retroalimentación a distancia, a tu maestra o maestro, cuando sea posible.
El reto del hoy:
Calcula el área de un trapecio cuyas bases miden 12 cm y 9 cm y su altura es de 7 cm. Representa la operación utilizando signos de agrupación y resuelve.
Asimismo, concluye los ejercicios pendientes que se realizaron en el desarrollo de la sesión y que se te pidió realizarás en casa.
Si te es posible contacta a tu maestra o maestro para compartir tus respuestas. Si ya tienes tu libro de Matemáticas de primer grado, ubica este tema y resuelve todo lo que puedas para comprender el tema. No olvides anotar tus dudas para que después sean resueltas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion