Hagámoslo más grande…

Aprendizaje esperado : identificación y aplicación del factor constante de proporcionalidad en casos sencillos.

Énfasis : identificar el factor constante de proporcionalidad al resolver problemas de escala.

¿Qué vamos a aprender?

Identificarás el factor constante de proporcionalidad al resolver problemas de escala.

¿Qué hacemos?

En nuestra sesión de hoy seguiremos revisando el factor constante de proporcionalidad y aprenderás cómo reproducir a escala un dibujo y a encontrar la relación que se presenta entre los lados de las dos figuras.

En un correo de Jorge, alumno de Aguililla, Michoacán. Nos dice que el paisaje en su comunidad ha cambiado. Porque antes viajaban a caballo o a pie, subiendo y bajando una montaña de grandes pinos.

Ahora su comunidad ya tiene un camino para vehículos, ha llegado el servicio eléctrico y el traslado al centro de salud es rápido. Sin embargo, no todo es bueno. El paisaje se ha deteriorado y cada vez hay menos pinos.

Por lo que, Jorge y sus compañeros se han organizado para sensibilizar a la comunidad de que hay que modernizarse, pero también hay que cuidar el medio ambiente.

Jorge explica que ha elegido un símbolo o logotipo para esta campaña ecológica. Ha seleccionado el dibujo de un pino y manda la siguiente imagen.

Jorge ha diseñado esta imagen de pino como símbolo de su proyecto, pero quiere reproducir otra más grande sin que se deforme la figura. Lo que quiere Jorge es una imagen más grande sin perder la forma de la figura de referencia, por eso, la pregunta es:

¿Cómo se puede reproducir la imagen del pino en tamaño más grande manteniendo una relación proporcional entre sus medidas?

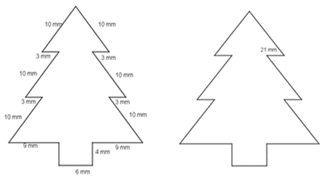
Jorge manda la figura original con sus medidas, y dice que quiere reproducirla, de tal manera que el lado que mide 3 mm mida 21 mm.

¿Qué hay que hacer primero?

Se debe reproducir el pino original a escala.

¿Qué significa reproducir una figura a escala?

Reproducir una figura a escala es hacer otra figura de igual forma, pero de diferente tamaño; es decir, una figura está a escala de otra cuando las medidas de los lados de ambas son proporcionales.

El problema para resolver es de escala.

Pon mucha atención, para empezar la reproducción de la figura, primero hay que calcular las medidas de los lados.

Calcularemos las medidas de la nueva imagen para reproducir una imagen a escala de la original.

Vamos a resolver este desafío. La pista es que el lado que mide 3 mm en la figura original en la nueva figura medirá 21 mm.

Analizando la figura, observamos que algunas medidas están repetidas. Las medidas son 3mm, 4mm, 6mm, 9mm y 10mm.

Ahora, con base en la pista y después de conocer las medidas de la figura de referencia, calcula las medidas de la nueva figura.

Veamos dos procedimientos:

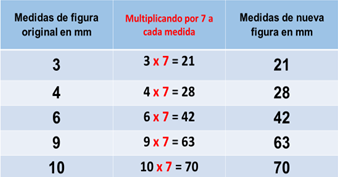
Procedimiento 1. Los cálculos de las medidas de la figura nueva son los siguientes:

Procedimiento 2. Aquí te muestro otros cálculos:

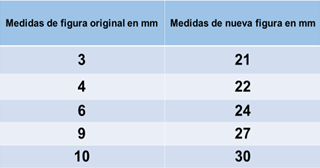
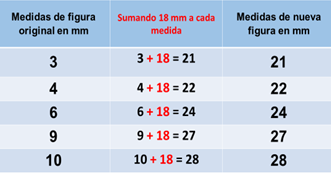
Procedimiento 1. En la tabla el lado que mide 3mm ahora debe medir 21mm y que aumentó 18mm. Así que, a cada medida se le aumentó 18 mm a cada medida de la figura original.

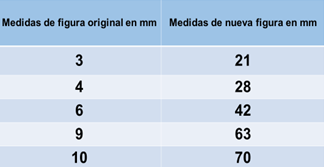
Procedimiento 2. En la tabla se encontró que entre el 3 y 21, hay una relación de división y dividiendo 21 entre 3, se obtiene 7. Así que a las demás medidas las multiplique por 7.

Ahora reproduciendo la figura de referencia con los datos encontrados en el procedimiento 1, veamos qué figura resulta.

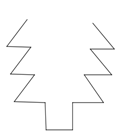
El pino no se parece al de Jorge, ¿Qué pasaría?

Los errores son también oportunidades para aprender. Aquí se ve que, sumando un mismo valor a las medidas dadas, la figura que resulta no es proporcional.

¡Ahora veamos la otra figura!

Procedimiento 2. En los cálculos de la segunda tabla, el pino sí muestra la proporcionalidad en sus medidas, es decir, sí está a escala.

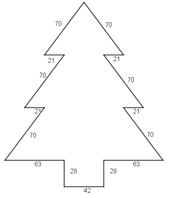
Fue importante presentarte los dos procedimientos. Hasta ahorita vemos que al sumar una misma cantidad a cada lado se obtienen datos erróneos y una figura deformada (procedimiento 1).

Multiplicar por una misma cantidad las medidas de todos los lados da como resultado otra figura más grande manteniendo la proporcionalidad (procedimiento 2).

Para recuperar lo aprendido, dime ¿Qué relación existe entre las medidas de la figura de referencia y las medidas de la figura construida?

Si piensas en la técnica usada para hacer la reproducción correcta. La relación entre las dos medidas de las figuras está en el número 7.

Porque el 7 es el factor común. Es el que se usó para obtener las medidas de la figura nueva, al multiplicarlo por cada medida de la figura de referencia, es decir que, las medidas de la figura nueva son siete veces mayores que las medidas de la figura de referencia.

La relación que existe entre las medidas de la figura de referencia y de la figura construida está dada por el factor común, que en este caso es 7.

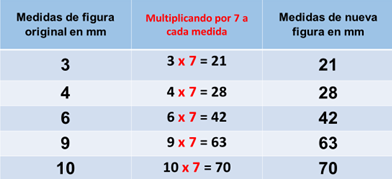
Para puntualizar la técnica para encontrar el factor común, responde, ¿Qué operación realizamos para encontrar las medidas de los lados de la nueva figura?

La respuesta es que usamos la división y la multiplicación. Porque primero dividimos la medida de un lado dada en la figura nueva, entre el mismo lado de la figura de referencia. Para obtener el número de veces que es más grande una que la otra.

Así obtuvimos el factor constante, que es el número 7 y lo multiplicamos por cada uno de los lados de la figura de referencia para obtener las medidas de la nueva figura.

Es momento de señalar lo aprendido en esta clase, después de esta experiencia matemática, puntualizaré algunas ideas importantes:

• El factor constante se usa para reproducir una figura en base a otra, manteniendo proporcionalmente sus medidas.

• Para reconstruir una figura mayor o menor a partir de otra, basta con identificar el factor constante y multiplicar o dividir según sea el caso.

• Has aprendido a usar el factor constante de proporcionalidad para resolver problemas de escala.

El reto de hoy:

Resuelve el desafío número 34 “Factor constante”, que se encuentra en la página 75, de tu libro de Desafíos Matemáticos.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

Descarga tu clase dando clic aquí