Habilidades matemáticas I. Lógica
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:24
Habilidades matemáticas I. Lógica
Aprendizaje esperado: desarrollar habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
Énfasis: desarrollar habilidades matemáticas. Lógica.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno de apuntes, lápiz y goma.
Además, se te recomienda anotar lo que consideres importante durante la sesión. Esto te permitirá llevar un orden en las actividades y retomar los temas con mayor claridad.
¿Qué hacemos?
El concurso de asignación a la Educación Media Superior es un proceso de selección que se realiza con una sola convocatoria para registrar a los aspirantes, y así evaluar sus habilidades y conocimientos en un único examen estandarizado.
En la zona Metropolitana de la Ciudad de México, este concurso es sustentado por la COMIPEMS o Comisión Metropolitana de Instituciones Públicas de Educación Media Superior, —que en conjunto con las instituciones participantes—, son los encargados de organizar y realizar todo el proceso de selección.

En éste participan las instituciones públicas de todo el país con procedimientos transparentes, equitativos e incluyentes, los cuales atienden la demanda de aspirantes y los ubica en alguna de sus opciones educativas con base en el número de aciertos y la disponibilidad de espacios.
Seguramente ya te estás preparándose para el examen de ingreso a nivel medio superior. Por ello, se ha decidido realizar una consolidación de saberes y habilidades a partir de esta sesión en la asignatura de Matemáticas que te sea de utilidad para tu preparación.
“Si un tren eléctrico va de Norte a Sur, ¿hacia qué lado echará el humo?”
Una condición para resolver este problema es leerlo atentamente para analizar, comprender y solucionar con un razonamiento lógico.
En ocasiones, si no se analiza el texto, se puede caer en los datos distractores —centrar la atención, por ejemplo, en la dirección de su trayecto, de norte a sur—, cuando la clave está en que esta maquinaria es un tren eléctrico que no echa humo.
De este modo, la respuesta es: Como es un tren eléctrico, no produce humo.
El razonamiento lógico es útil para diversas situaciones de la vida cotidiana; es la base para un pensamiento ordenado el cual permite llegar a conclusiones elaboradas.
Durante la sesión trabajarás situaciones no rutinarias, es decir, problemas que se resuelven con un razonamiento lógico, como el ejemplo anterior.
Para abonar en estos conceptos, resuelve la siguiente situación:
Fernanda tienen 4 hijos y uno de ellos se comió un pastelito que dejo en el congelador. Al preguntar a sus hijos “¿Quién se comió el pastelito?”, ellos responden:

Conociendo que solo uno de ellos dice la verdad, piensa ¿quién se comió el pastelito?
Para resolver este tipo de problemas es conveniente utilizar tablas de posibilidades.
En ella se le asigna un valor de “verdadero o falso” a cada proposición y a partir de este, se deducen los valores de verdad en las demás proposiciones. En tanto que, si no existen contradicciones, se llega a la solución buscada.
Apoyados en la tabla de posibilidades con el nombre de cada hijo, se asignan los siguientes valores de verdad:
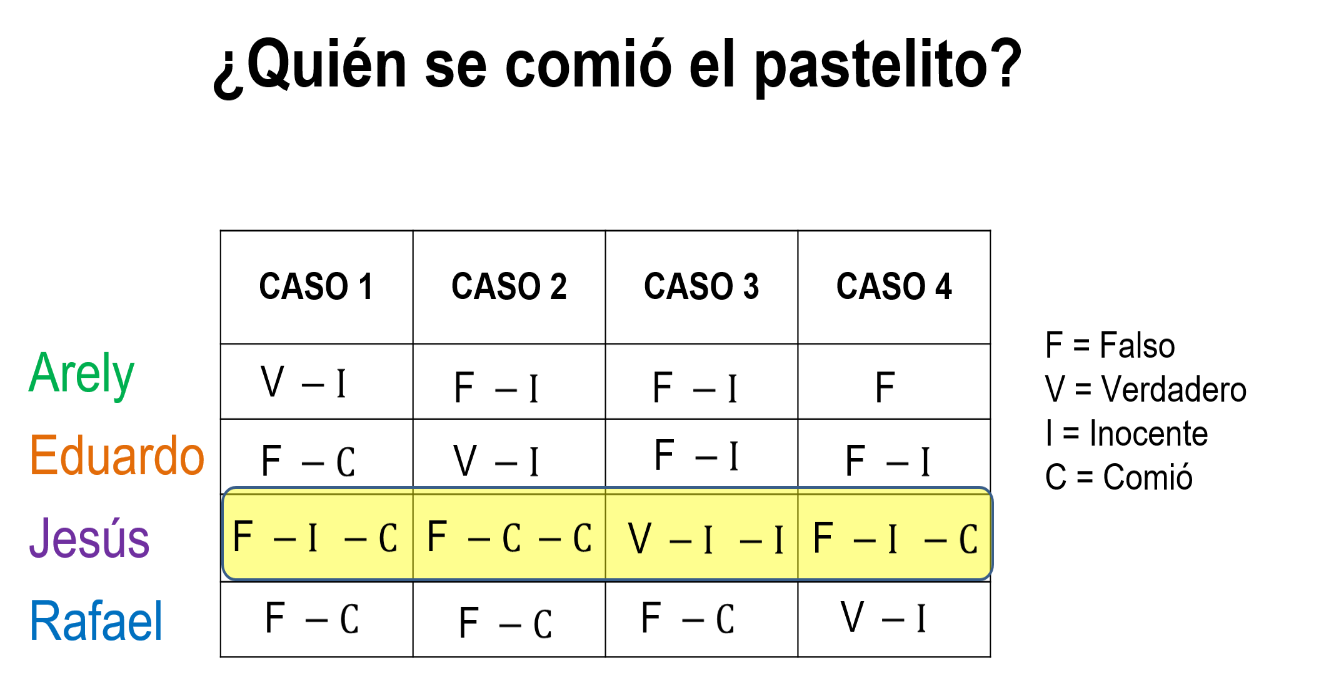
Caso 1:
Si supones que Arely es la que dice la verdad, es inocente. Entonces, Eduardo y Rafael se lo comieron, y Jesús sería Inocente y culpable a la vez, lo cual es imposible, por lo que se descarta la posibilidad.
Caso 2
Si Eduardo fuese el que dice la verdad, él sería inocente al igual que Arely. Entonces, Jesús y Rafael se comieron el pastelito —y como es uno solo quien se lo comió—, se descarta esta posibilidad.
Caso 3
Si Jesús dijera la verdad, se deduce fácilmente que Arely, Eduardo y Jesús son inocentes, y solo Rafael aparece como el único que se lo comió. Por lo tanto, es una posible solución.
Caso 4
Si Rafael dijera la verdad, se llega rápidamente a una contradicción, pues Jesús sería al mismo tiempo inocente y la persona que se lo comió, lo cual es imposible.
De este modo, se concluye que el único quien no llega a una contradicción es en el Caso 3. Entonces, Rafael se comió el pastelito
Los problemas de razonamiento lógico son aquellos que no dependen tanto del contenido matemático sino del razonamiento natural, adecuado y correcto.
Para muestra se tiene otra situación.
Un señor se encuentra en la orilla de un río con un perro, una gallina y una bolsa de maíz.
El señor desea cruzar el río con sus tres pertenencias y para lograrlo, dispone de una balsa en la que necesariamente debe ir él y solo una de las tres cosas que desea llevar consigo.
El problema consiste en pasar al perro, a la gallina y la bolsa de maíz al otro lado, pero cuidando que nunca se quede sola la gallina con el maíz —porque la gallina se lo come—, ni el perro con la gallina, ya que el perro se la comería.

¿Qué debe hacer el señor para llevar en su balsa a la gallina, al perro y al maíz sin sufrir pérdida alguna?
Toma en cuenta que, al pasar al perro, a la gallina y la bolsa de maíz del otro lado, nunca se puede quedar sola la gallina con el maíz, ni el perro con la gallina, pues en ambos casos, se las comerían.
¿Ya pensaste en una solución? Podría ser que pases primero a la gallina.

En algunas ocasiones para resolver problemas de razonamiento lógico es conveniente utilizar un principio elemental, pero indispensable que se le conoce por distintos nombres: “Principio de Dirichlet”, “Principio de las casillas”, de las gavetas, de palomares, por mencionar algunos.
Para ejemplificar este principio, imagina que “n” palomas se distribuyen en “m” palomares.

Otra forma en el que se presenta es: Hay 9 huecos para albergar máximo 9 objetos, siempre y cuando cada uno de los objetos está en un hueco distinto.
Si se quiere añadir otro objeto, se fuerza a volver a utilizar alguno de los huecos.
Se resuelve una situación donde sea conveniente utilizar el principio de los palomares.
En una gaveta, dentro de una habitación totalmente oscura, hay 120 calcetines de 4 colores diferentes.
¿Cuál es el menor número de calcetines que se debe de extraer para poder asegurar que se tiene al menos un par de calcetines del mismo color?

El número mínimo de calcetines a extraer para estar seguros de tener un par del mismo color es 5.
Pues a lo sumo, se pueden sacar cuatro calcetas de colores diferentes, pero la quinta debe de coincidir con uno de los cuatro colores anteriores y formar un par del mismo color.

Algunos problemas de razonamiento lógico se resuelven con pocos elementos de contenido matemático, mientras que en otros es necesario analizar los elementos con los que se trabaja. Por ejemplo, cuando se opera con números pares e impares.
Por ejemplo:

Si se analizan cuidadosamente —sólo observando las cifras que se encuentran en la posición de las unidades—, se reconoce si son pares o impares:
Número par más número par es igual a un número par.
Número impar más número impar es igual a un número par.
Número impar por número impar es igual a un número impar
Y número par por número par es igual a un número par.
Considerando lo anterior, se resuelve la siguiente situación.
En una bolera o juego de boliche hay 10 bolos. Por cada bolo que se derribe se obtiene un número de puntos igual al que se muestra en la imagen.
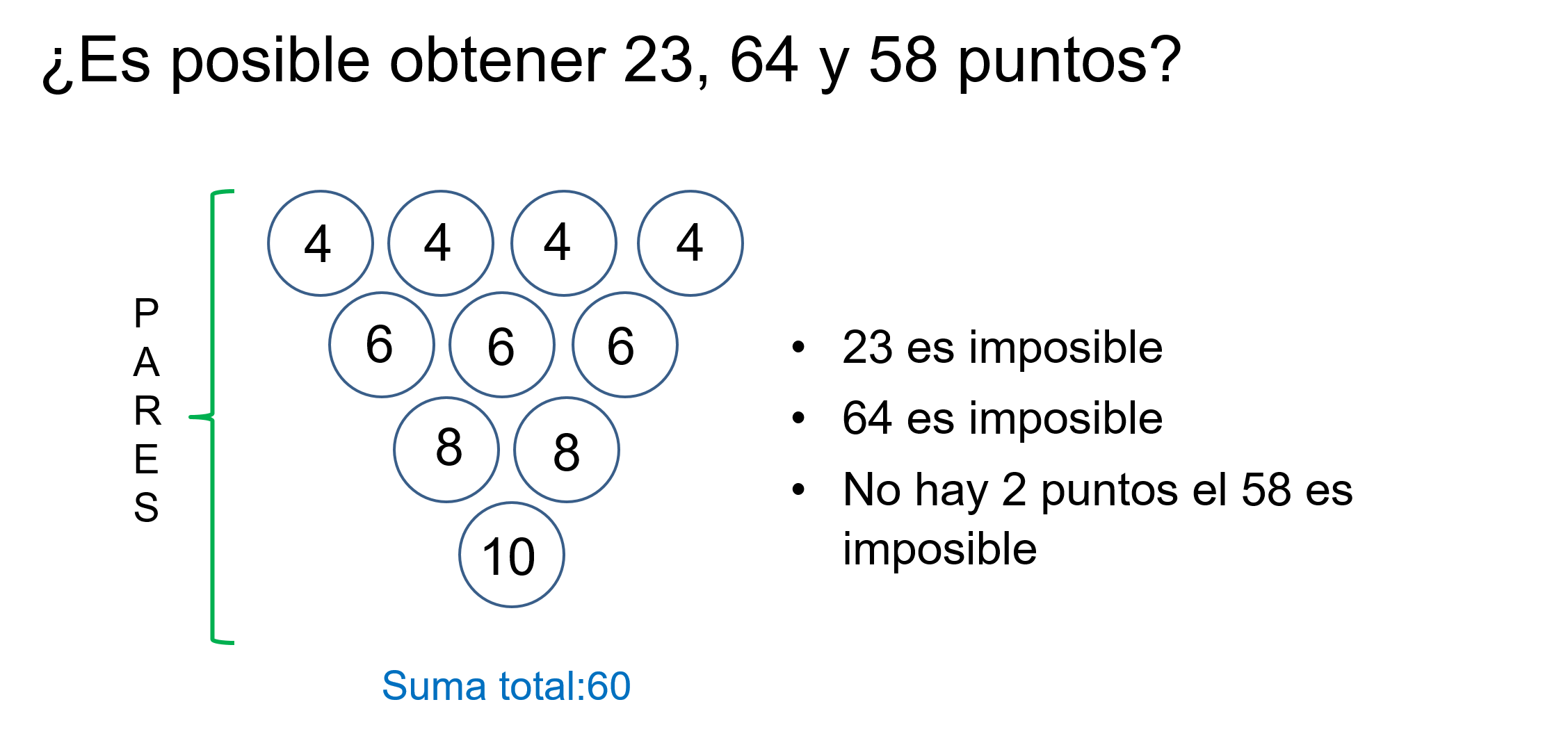
Sabiendo esto, ¿es posible obtener 23, 64 y 58 puntos?
Todos los puntos son pares, por lo tanto, el 23 es imposible.
Como la suma es 60, el 64 es imposible.
Y como no hay 2 puntos, el 58 es imposible, ya que el segundo número más grande que se puede obtener es 56, al dejar en pie uno de 4.
Por lo tanto, no es posible obtener 23, 64 ni 58 puntos.
Se sigue con una situación más:
Tres amigos van a una cafetería y piden tres cafés.
Cuando llaman al mesero y piden la cuenta, el mesero les dice que son 25 pesos.
Cada uno pone 10 pesos y el mesero les regresa 5 pesos en monedas de 1 peso.
Los tres amigos se reparten 1 peso para cada uno y los 2 pesos restantes se los dejan de propina al mesero.
Si cada amigo pagó 9 pesos —es decir, 10 menos 1 peso de cambio—, entonces pagaron entre los tres: 9 por 3 igual a 27 pesos, más 2 pesos de propina al mesero son 29 pesos. Entonces:
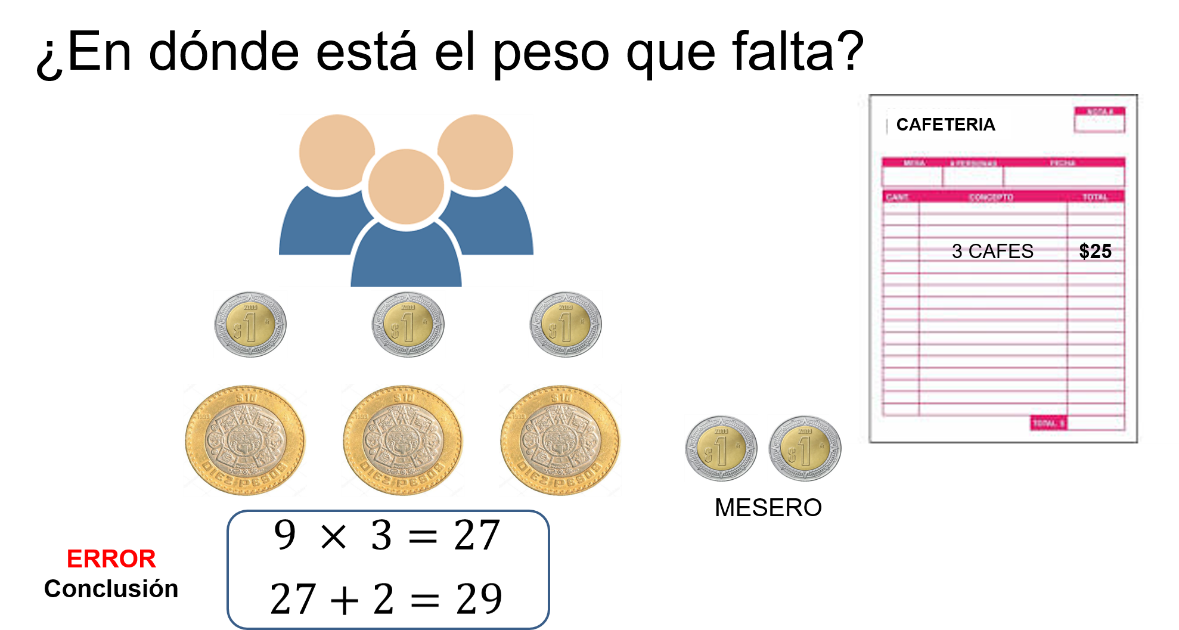
Se analiza la situación para reconocer el error en la conclusión y así encontrar el peso faltante.
No se deben de sumar 27 pesos más 2 pesos porque los 2 pesos de propina son parte de los 27 pesos que pagó cada uno.
Por lo tanto, lo correcto, es decir: Cada uno gastó 9 pesos; si se multiplica por los 3 es igual a 27 pesos, más 3 pesos de cambio son los 30 pesos iniciales.
Existen problemas como éste en donde se hace una conclusión camuflada como válida, por la cual no se tienen dudas de que así sea.
Por el contrario, también representa aquel momento del problema en donde se produce el engaño. Por ello es importante leer y analizar el problema, y usar la lógica para darle solución.
Existen problemas relacionados a la teoría de la aritmética que, a partir de los conocimientos fundamentales, se pueden razonar en forma lógica para desarrollar la actividad mental.
Sumado a lo anterior, se tiene un ejemplo que lo ilustra.
Un enfermo debe de tomar un medicamento cada 8 horas, ¿en cuánto tiempo lo tomará 5 veces?
Intuitivamente, muchos al tratar de responder rápido, contestan 5 por 8, 24 horas. Esto sucede porque en común no se considera que el conteo del tiempo inicia al tomar el medicamento la primera vez, por lo que faltan 4 tomas cada 8 horas, teniendo un total de 32 horas.
En consecuencia, 5 tomas del medicamento llevan un total de 32 horas.

La Geometría es muy rica en razonamientos y contribuye al desarrollo del pensamiento lógico. Por ello, se aprovechan todas sus potencialidades para incluir conocimientos esenciales de la misma.
Resuelve la siguiente situación:
¿Cómo se pueden distribuir 24 personas en 6 filas de modo que en cada fila estén 5 personas?

Al analizar la situación planeada, se considera la posibilidad de filas disjuntas, es decir, sin elementos comunes, como cuando estás en el salón de clases.
Pero de esta forma, cada fila puede tener solo 4 personas, lo que hace pensar que éstas deben tener elementos comunes.
Se busca entonces, una figura geométrica que pueda dar solución al problema.
Necesariamente, se piensa en un hexágono para poder formar 6 filas con un elemento en común “dos a dos”, como se registra en la imagen.
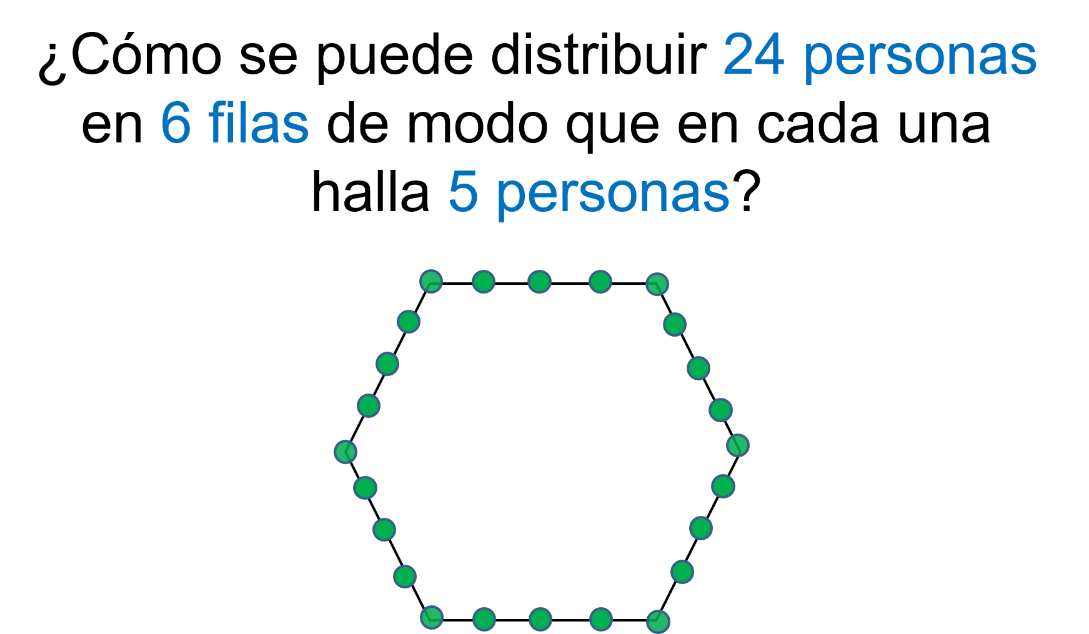
En la Teoría de Conjuntos, una de las cuestiones fundamentales es determinar los elementos que componen un conjunto a partir de una propiedad o característica esencial del mismo.
Se tiene así, una situación que ilustra lo anterior con mayor claridad.

La propiedad esencial de este conjunto es la de ser rectángulos —solo se hace referencia a la forma y no a las dimensiones—.
Entonces, para determinar cuántos elementos tiene el conjunto, se debe de precisar cuántos rectángulos hay, sin importar sus dimensiones.
Se hace notar que las paralelas medias determinan 4 rectángulos. Además, tomando la paralela media horizontal como lado común, quedan determinados otros 2 rectángulos.
De igual forma, la media vertical determina 2 más y, por último, el rectángulo mayor que contiene todos los anteriores.
Después de este análisis, se puede concluir que hay 9 rectángulos en la figura.
A continuación, resuelve una situación más.
Se quiere saber cuánto suman una manzana más un racimo de uvas, más un plátano.
Se sabe que la manzana es igual a 7, el racimo de uvas es igual a 5 más la manzana, y la manzana es igual a 1 más 3 plátanos.
¿Cuánto sumarán una manzana más un racimo de uvas y un plátano?
Si se observa la imagen, la manzana tiene un valor de 7 y el racimo de uvas es igual a 5 más una manzana. Es decir, 5 más 7 igual a 12, por lo que el racimo de uvas vale 12.
Por otra parte, la manzana es igual a 1 más 3 plátanos; si la manzana vale 7, los 3 plátanos deben de valer 6 para que sumados con 1 den 7.
La pregunta es: ¿Cuánto suman una manzana más un racimo de uvas, más un plátano?
Se tiene así que la manzana vale 7, el racimo de uvas 12, y 3 plátanos valen 6.

Pero en la sumatoria solicitan únicamente un plátano, por lo que se suman 7 más 12, más 2, igual a 21.
La suma de una manzana más un racimo de uvas, más un plátano es igual a 21.
Es posible que mientras se resolvían los problemas, identificaste que en la guía de estudio para ingreso a Nivel Medio Superior existen algunos reactivos similares.
Como una actividad adicional, comenta con tus familiares por qué se les llaman “reactivos de razonamiento lógico matemático”.
A continuación, se resuelven algunos reactivos de habilidad lógico matemático.
En este reactivo solicitan identificar cuál de las opciones representa la palabra “murciélago”.
Al analizar las opciones, todas coinciden en que el primer símbolo es un corchete, por lo que representa a la letra “M”.
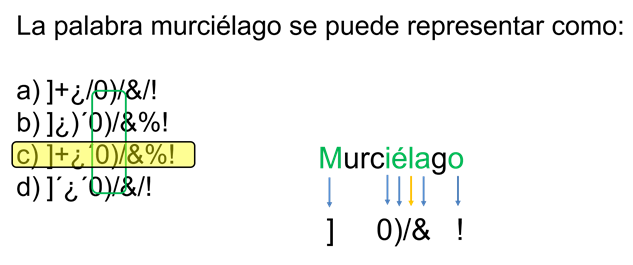
Asimismo, todas las respuestas coinciden con los símbolos enmarcados por el recuadro verde, y el ultimo símbolo es el mismo, por lo que representa a la letra “o”. De este modo, de la palabra “Murciélago” solo faltan descubrir 4 letras.
Observa en los incisos “a”, “b” y “d” cómo tienen más de una diagonal, lo que es imposible, porque la diagonal representa la letra “L”. Por lo tanto, la respuesta correcta es el inciso “c”.
Resuelve otro reactivo.
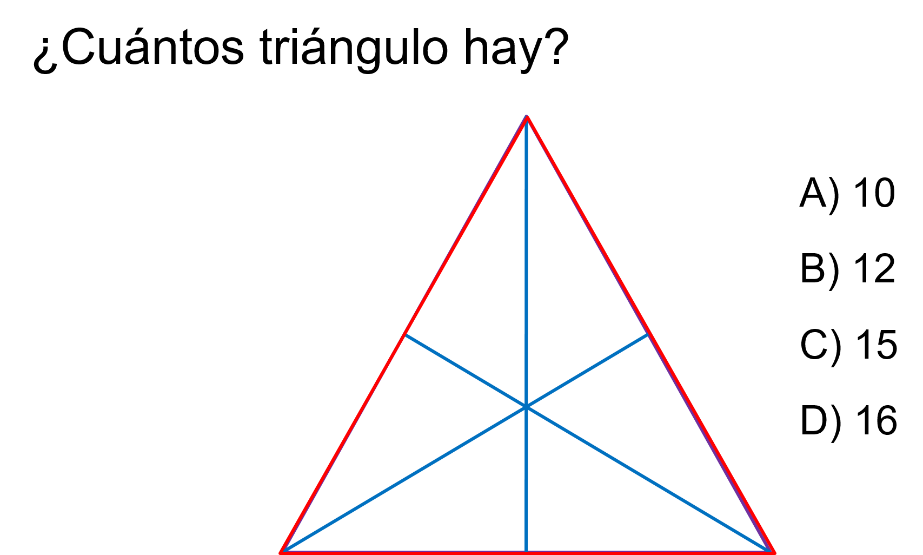
En una primera impresión, hay 6 triángulos pequeños, los cuales son cada uno de los sextos que conforman la figura dividida.
Sin embargo, analizando la figura, se puede observar que hay 10 triángulos más: 3 triángulos isósceles que son tercios; 6 triángulos que representan las mitades y el triángulo equilátero. En total son 16 triángulos, entonces la respuesta correcta es el inciso “D”.
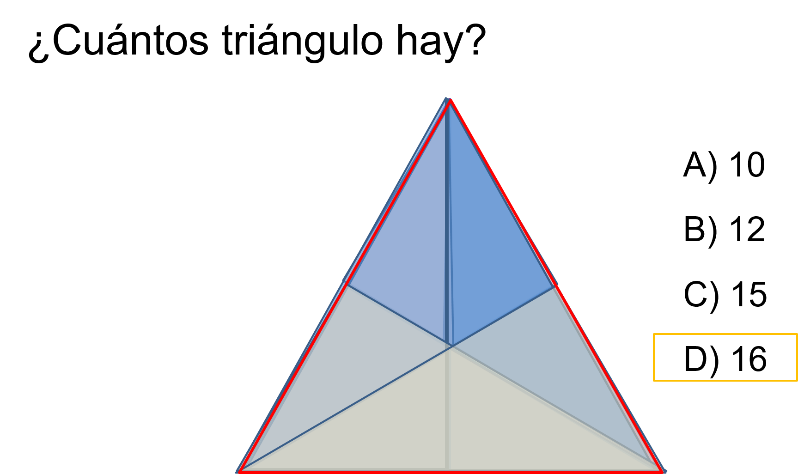
Pero al analizar la figura se observan 10 triángulos más: 3 triángulos isósceles que son tercios; 6 triángulos que representan las mitades y el triángulo equilátero.
Obteniendo un total de 16 triángulos, por lo que la respuesta correcta es el inciso D.
Puedes reconocer que este reactivo era similar al de los rectángulos.
Continúa con la solución de reactivos tipo “Examen de Ingreso para Nivel Medio Superior”.
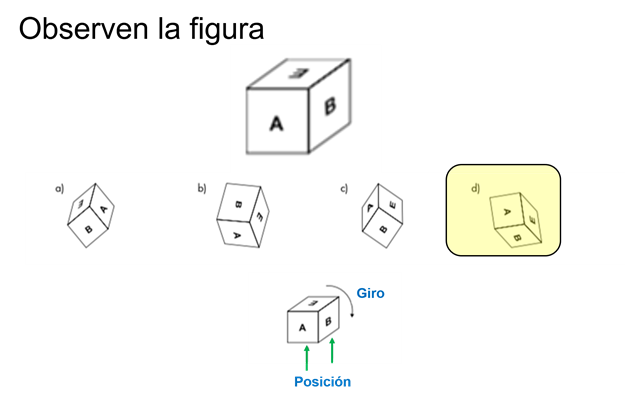
¿Cuál de las siguientes figuras corresponde a la anterior después de ser girada?
De la figura inicial se analiza la posición que guardan las letras y enseguida, el giro que se dio a la figura. Por esa razón, la opción correcta es el inciso “D”.
Resuelve un último reactivo:
Una pieza rectangular de papel se dobla dos veces y se corta a la mitad un círculo, como se muestra en la figura.
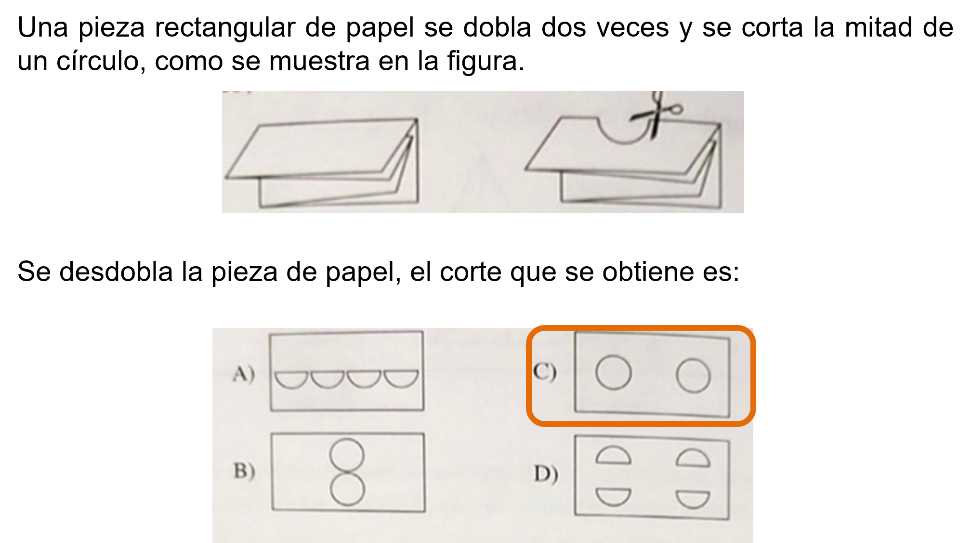
Analiza las cuatro opciones. Es importante imaginar sin necesidad de realizar el experimento con una hoja de papel y tijeras.
Al desdoblarla los círculos quedan en el centro, por lo tanto, se llega a la conclusión de que la respuesta correcta es el inciso “C”.
Se destaca que el pensamiento lógico matemático es fundamental para comprender conceptos abstractos, razonamiento y comprensión de relaciones.
Todas estas habilidades van más allá de las Matemáticas entendidas como tales; los beneficios de este pensamiento contribuyen a un desarrollo sano en muchos aspectos y en consecución: Las metas, los logros y el éxito personal.

Como te habrás dado cuenta, son interesantes las estrategias presentadas para el desarrollo del pensamiento lógico-matemático.
Consulta las diversas guías de estudio, así como revisa algunos otros problemas en libros o sitios de internet para reforzar lo aprendido.
El reto de hoy:
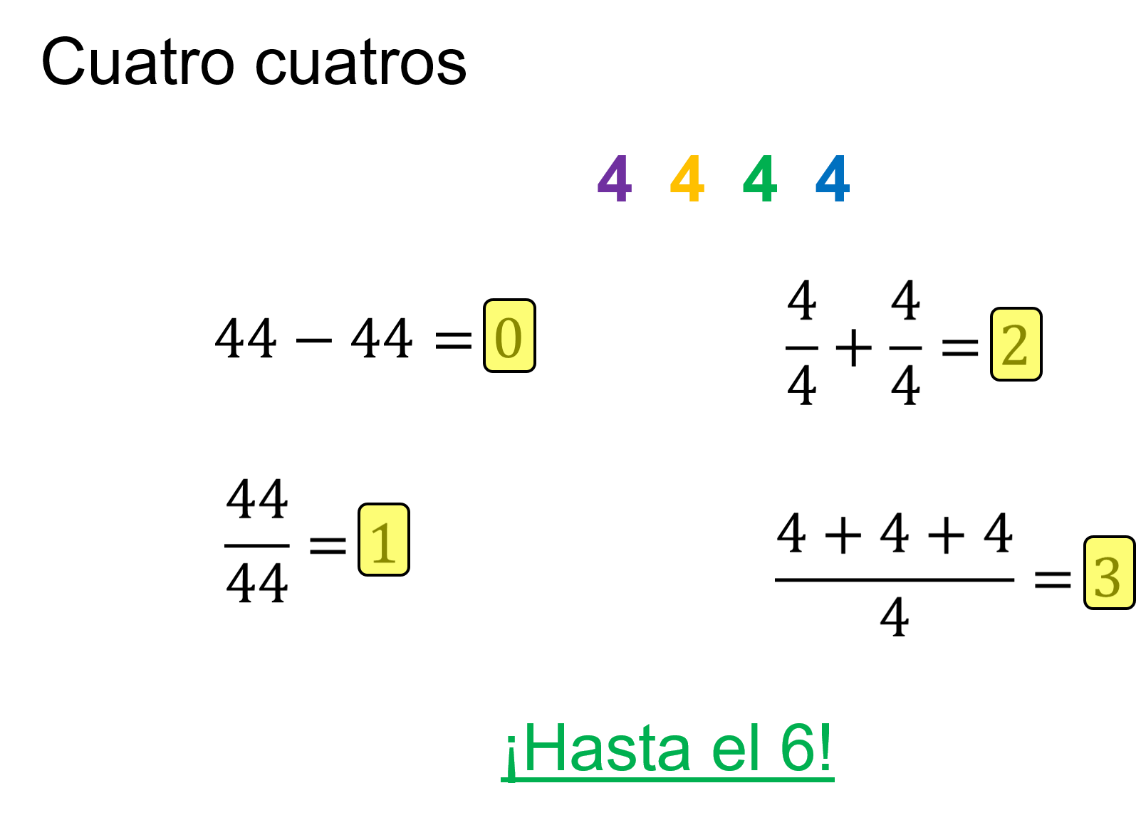
El ejercicio consiste en encontrar la forma para representar los números del 0 al 6, usando para ello solo cuatro 4, es decir, cuatro números cuatro, y a lo sumo, algunos símbolos para las operaciones básicas, por ejemplo:
Para formar el cero, se resta 44 menos 44.
Para formar el 1, se puede dividir 44 entre 44.
Para formar el 2, se suman “cuatro cuartos” más “cuatro cuartos”.
Para formar el 3, se suma 4, más 4, más 4, más 4, y todo entre 4.
El reto es representar el resto de los números hasta llegar al 6.
Una vez realizado, se te sugiere enviarlo a tu maestra o maestro de Matemáticas y también a tus compañeros para que compartan la manera en la que lo resolvieron.
Se te recomienda estudiar para el examen de ingreso a nivel medio superior, buscando un buen lugar en casa para reducir los distractores. De igual manera, si está a tu alcance, acude a exámenes de simulación para que te prepares lo mejor posible.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.





Login to join the discussion