François Viète y el álgebra simbólica
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
François Viète y el álgebra simbólica
Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.
Énfasis: reconocer las aportaciones de François Viète al algebra en la conceptualización del número simbólico.
¿Qué vamos a aprender?
El día de hoy conocerás a uno de los matemáticos más importantes de la historia, a François Viète, quien realizó contribuciones significativas al lenguaje del álgebra para que, junto con otros matemáticos, se construyera esta disciplina tal como se conoce en la actualidad.
¿Qué hacemos?
Para iniciar conocerás la vida y obra del matemático François Viète.
François Viète, también conocido por su nombre españolizado como Francisco Vieta, nació en Fontenay le Comte, Francia, en el año 1540 y murió en París, Francia, el día 13 de febrero de 1603.

Se educó en la universidad de Poiters desde 1558, donde se graduó en leyes.
Perteneció a una familia burguesa de una amplia tradición en el estudio de las leyes. Fue un notable abogado que se codeó con importantes figuras como los reyes de Navarra, el reino de Navarra se ubicaba en los pirineos, una cordillera en la frontera entre España y Francia. Asimismo, socializó con distinguidas familias de otros lugares, como Parthenay, Francia. De ahí que en 1564 pasara a ser profesor de Catherine de Parthenay, con la que seguiría unido toda su vida.
También estuvo al servicio de la casa de Soubise, otra comuna en Francia, como secretario particular encargado de defender los intereses de la familia Soubise.
En 1569, François Viète se convirtió en abogado, por lo que se tuvo a bien confiarle asuntos muy importantes de Fontenay-le-Comt, su lugar de nacimiento. Entre otros, la liquidación de las tierras en la región de Poutio, región de Francia, que pertenecían a la viuda del rey Francisco I, así como velar por los intereses de la reina de Escocia, María Estuardo.
Se desempeñó como abogado en el Parlamento de París, entre los años de 1573 y 1582, y también fue consejero del rey Enrique III de Francia y de su primo y sucesor Enrique IV de Francia. Se le conocía como súbdito del rey y se le considera por su lealtad y competencia. En 1580, pasó al servicio exclusivo del rey en el Parlamento de París.
Sirvió constantemente a ambos monarcas como criptógrafo y, utilizando constantemente el álgebra en la criptografía, buscó decodificar mensajes de países rivales y vecinos a Francia, esto le permitió decodificar los mensajes cifrados de la corona española.
En 1584, a Vieta se le apartó de sus funciones por razones políticas y religiosas. Enrique de Navarra, un amigo de Vieta, redactó varias cartas en su favor, intentando que recuperara su puesto al servicio del rey, pero no fue escuchado. Vieta, dedicó esos años, apartado de la vida política, a las matemáticas.
Tras la muerte de Enrique III, Viète pasó a formar parte del consejo privado de Enrique IV, quien lo admiraba por su talento matemático. A partir de 1594 se encarga exclusivamente de descifrar los códigos secretos enemigos, tarea que venía desarrollando desde 1580.
En 1590, Enrique IV hizo pública una carta del comendador Moreo al rey de España y cuyo contenido Viète había descifrado. La carta revelaba que el jefe de la Liga Católica en Francia, el duque de Mayenne, aspiraba a convertirse en rey en lugar de Enrique IV.
Este matemático francés fue uno de los principales precursores del álgebra. Sin embargo, los primeros trabajos que realizó en el campo de las matemáticas, entre los años de 1564 a 1568, giraban en torno a la astronomía y la trigonometría.
Como los matemáticos de su época, Viète se sentía continuador de las matemáticas griegas, que son fundamentalmente cuestiones geométricas, por ello hizo estudios y observaciones muy importantes que dieron un amplio impulso a la geometría y a la trigonometría. En 1570 dio a la trigonometría su forma definitiva en una obra titulada Canon mathematicus.
 |
 |
En 1591 publicó la obra In artem analyticem isagoge, que significa Introducción a las habilidades analíticas, en el cual introdujo un sistema de notación que hacía uso de las letras en las fórmulas algebraicas.
De hecho, fue Viète el primero en aplicar las letras para representar una ecuación. Los matemáticos utilizaban las letras para representar variables, pero no así para representar parámetros o lo que se puede llamar número algebraico.

A continuación, revisarás una ejemplificación de una asesoría de François Viète a un alumno de secundaria. En este diálogo podrás descubrir una de las más grandes aportaciones de Viète a las matemáticas.
Alumno:
¡Creo que no estoy entendiendo nada! Pero, no importa porque aquí me encuentro con el verdadero licenciado François Viète. Fíjese que estaba viendo su documental porque me dejaron realizar una tarea de matemáticas; pero no le entendí, por eso mejor lo llamé a usted, para que me diera unas clasecitas particulares.
Viète:
Qué bueno que me llamaste, ¿cuál es la tarea que te dejaron?
Alumno:
El problema que me dejaron es el siguiente:
Si tienes la suma y la diferencia de dos números cualesquiera, demuestra que puedes encontrar siempre cuáles son esos dos números.
Viète:
¿Y no tienes ni idea de cómo se resuelve?
Alumno:
No, por eso lo llamé, maestro.
Viète:
¿Pero cómo es posible? Si ya vas en segundo grado de secundaria.
Alumno:
Bueno, yo le dije a mi profesor de la escuela que podíamos suponer cuál es la suma y la diferencia de dos números.
Viète:
A ver, explícame eso.
Alumno:
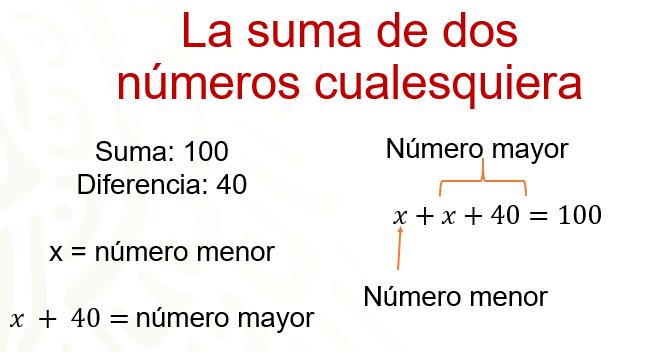
Le explique al profesor, que se podía suponer que la suma de dos números es, por ejemplo, 100 y su diferencia es 40.
Entonces, aplicando estos conocimientos de álgebra, se puede suponer que el número menor es “x” y entonces el mayor es “x” más 40.
Viète:
De acuerdo, pero primero pon un ejemplo con números naturales en lugar de la equis, Como tú maestro es mi responsabilidad asegurarme de que entiendes de lo que estás hablando.
Alumno:
Está bien, profe Viète. A ver, dígame dos números cualesquiera.
Viète:
¿Tú me vas a preguntar a mí? Está bien, a ver, dos números… “m” y “n” o “a” y “b”.
Alumno:
No, profe Viète, dos números normales.
Viète:
Dijiste dos números cualesquiera. Entonces lo que tú quieres son dos números naturales, naturales no normales. Está bien, 30 y 20.
Alumno:
La suma de esos números es 50 ¿no? Entonces si el menor es 20, el mayor debe ser 20 más 30 que se supone es la diferencia. ¿Está de acuerdo?
Viète:
Sí, ¿y luego?
Alumno:
Entonces vuelvo a la solución que le propuse al profe de mi escuela: suponiendo que la suma de dos números es 100 y su diferencia es 40, por lo tanto, si el número menor es “x”, el mayor es “x” más 40.
Viète:
¡Pero miren! si no es tan malo en matemáticas. Prosigue, ¿entonces?
Alumno:
Entonces, como el número menor es “x” y el mayor es “x” más 40 y la suma de estos dos números es 100, se puede formar la ecuación “x” más “x”, más 40 igual a 100. ¿Voy bien, profe Viète?
Viète:
Sí, estoy viendo por dónde vas, lo que has dicho es matemáticamente correcto.
Alumno:
De la ecuación “x”, más “x”, más 40 igual a 100, la reduzco como me enseñó mi otro profe y resulta 2 “x” más 40 igual a 100.
Viète:
Hasta ahora, muy correcto jovencito, sigue adelante.
Alumno:
Ahora, para despejar “x” resto 40 de cada lado de la igualdad y luego, a lo que obtengo, lo divido entre dos y resulta finalmente…
Viète:
¡A ver, jovencito, ahora si te voy a interrumpir!
Alumno:
¿Qué pasó, profesor?, ¿voy mal?
Viète:
No, no vas mal, y aunque se obtenga el mismo resultado, te voy a exigir que uses mi método de resolución de ecuaciones, si no ¿para qué lo inventé?
Alumno:
A ver, a ver. ¿Cómo va?
Viète:
Mi método es más fácil y más sintético. Mira, tienes al 40 sumando del lado izquierdo de la igualdad ¿no? Bueno, pásalo al lado derecho con la operación inversa, es decir, restando.
Te queda 2 “x”, igual 60. Luego, como el 2 multiplica a la “x”, pásalo del otro lado dividiendo, es decir, sólo aplica la operación inversa del otro lado y listo, 60 entre 2 es igual a 30. ¡Tenemos como resultado 30!

Alumno:
Guuaauu, maestro Viète, ahora sí se lució.
Viète:
Claro que sí. Está bien que sepas la otra forma de resolver la ecuación, porque así es claro para ti de dónde salió el método que inventé.
Alumno:
Lo que le dije a mi otro profe es que los números que buscaba son 30 y 70, ya que, si a 30 se le suman 40, pues da 70.

Además, la suma de estos dos números es 100 y su diferencia es 40. Pero él dice que estoy mal, bueno, que no es totalmente correcto.
Viète:
Pues claro que estás mal, en realidad no hiciste la tarea que te pidió.
Alumno:
¿No entiendo por qué?
Viète:
Fíjate bien. Dice que, si tienes la suma y la diferencia de dos números cualesquiera, no dice de 100 y de 40, como tú lo hiciste.
Alumno:
¡Ah sí! Pero yo puedo repetir este procedimiento con otros números, como 50 y 20 o 300 y 90.
Viète:
Ah, sí. Y con 4 y 15 y con 60 y 80, y no terminarías, porque los números son infinitos.
Alumno:
¿Quieres que te muestre que funciona con otros números?
Viète:
No, el tiempo es valioso y ya casi se termina mi asesoría. Pero no lo puedes hacer con todos los números.
Alumno:
Pues no, pero mire, profe Viète, la verdad no le estoy entendiendo.
Viète:
¡Ay! Es que tú estás pensando igualito que Diofanto, un gran matemático que yo conozco, que nació en Alejandría, y que, como tú, dice que no entiende lo que es una solución general.
Alumno:
A ver, explíquese profe Viète.
Viète:
La clave del problema está en donde dice: si tienes la suma y la diferencia de dos números, esta suma y esta diferencia son dos números cualesquiera, no dice que sea 100 y 40 u otros números en específico.
Alumno:
¡Ah! Entiendo, pero entonces ¿cómo lo resuelvo?
Viète:
Pues tienes la suerte de que yo inventé el concepto de número algebraico, ya que en mi tiempo sólo se conocían las variables como las que conoces, que se representan en la actualidad con “x” o con “y”, con esto que inventé se pueden resolver problemas como el que te dejaron de tarea. Mi contribución a las matemáticas fue mostrar que todos los problemas, claro, los de mi tiempo, se podían resolver mediante ecuaciones algebraicas.
Alumno:
¡Qué bien! Y eso que escuché que era usted abogado.
Viète:
Sí, efectivamente, pero también me gustan las matemáticas, y cuando, por ganarle un pleito legal a un Duque, me retiraron de mis funciones de abogado, me dediqué completamente a las matemáticas. Pero bueno, sigamos con la clase que ya casi me tengo que ir.
Alumno:
¡Qué interesante su vida! Pero me decía que la solución al problema era ver a la suma y la diferencia como números algebraicos.
Viète:
Exactamente, aunque en mi época a dichos números los llamé especies. Bueno, pues usando especies, digo, números que también podemos llamar simbólicos, en lugar de 100 y 40 tenemos que suponer que “a” es la suma y “b” es la diferencia. Podemos ir comparando estos números con los que tú propusiste.
Por lo tanto, si el número menor es “x”, entonces el mayor será “x” más la diferencia. Con números específicos el mayor sería “x” más 40, porque 40 es la diferencia, pero con números simbólicos sería “x” más b.

Alumno:
Bien, lo sigo.
Viète:
Entonces, la suma de los dos números, el menor, o sea “x”, y el mayor, “x” más “b”, sería “x” más “x”, más “b”, pero como se dijo que la suma de esos números es “a”, se forma la ecuación “x” más “x”, más “b” igual a “a” y simplificando la ecuación queda 2 “x” más “b” igual a “a”, porque, como tú sabes, “x” más “x” es igual a 2 “x”.

Alumno:
A ver, yo resuelvo ahora la ecuación. Déjeme ver si aprendí su método de resolución de ecuaciones. Entonces, paso la “b” restando del otro lado de la igualdad y me queda 2 “x” igual a “a” menos “b”. Luego, como estos números son simbólicos y no son iguales, no se pueden reducir, como 30 y 40; entonces, pasando el 2 dividiendo del otro lado de la igualdad resulta “x” es igual a “a” menos “b”, entre 2.

Viète:
Muy bien, “x” es igual a “a” menos “b” entre 2, pero este es el número menor. Ahora hay que buscar simbolizar el número mayor y lo que debes hacer es ir comparando nuevamente estos números simbólicos con los números específicos que tú propusiste.
Alumno:
Hay que hacerlo porque esos números algebraicos o simbólicos no me son tan familiares.
Viète:
Entonces, tú propusiste que el número menor fuera “x” y el número mayor “x” más 40, es decir, “x” más la diferencia, que es 40.
Alumno:
Sí lo recuerdo, de hecho, obtuvimos que “x” es 30, o sea el número menor es 30.
Viète:
Ahora bien, con números simbólicos se obtiene que “x”, en lugar de valer 30, valía: “a” menos “b”, entre 2. Luego, con los números que tu propusiste, a 30 le sumas la diferencia dada que era 40, pero aquí a…
Alumno:
…“a” menos “b” entre 2, le debes sumar la diferencia dada, que es “b”, porque son tus famosas especies o números algebraicos.

Viète:
¡Muy bien! Pero ¿cuánto es “a” menos “b” entre 2, más “b”?
Alumno:
¡Eso no lo sé! Profe Viète, apenas voy en segundo, explíqueme por qué se ve muy difícil.
Viète:
¡Tienes razón! Pero no es tan difícil porque ya sabes cómo resolver una suma de fracciones, sólo que aquí lo harás con mis famosos números algebraicos, que también les llamé números simbólicos.
Alumno:
Bueno, a ver dígame cómo.
Viète:
El primer número, “a” menos “b” entre 2 se ve como fracción porque tiene el denominador 2, pero el segundo número “b” no se ve como una fracción, pero sí lo puedes ver así:

Alumno:
¿Cómo que también es una fracción? ¿De verdad?
Viète:
Mira, si colocas la unidad, es decir, el número 1 como denominador, se vuelve una fracción.
Alumno:
Pero ¿eso no afecta al valor de “b”?
Viète:
¡Claro que no!, recuerda que “b” es un número algebraico y puede también ser cualquier número, al igual que las variables que tú conoces, entonces, ¿cuánto será “b” entre 1?
Alumno:
Pues “b”, pero, ¿para qué ponerle el 1 como denominador?
Viète:
Para que repases el procedimiento de resolución de fracciones, que seguramente ya conoces.
Alumno:
Ah, sí, sí. Se obtiene el común denominador, se divide entre el numerador de la primera.
Viète:
Vamos haciéndolo paso a paso con esta suma de fracciones algebraicas. Y tú me vas diciendo qué hacer. ¿Te parece?
Alumno:
El común denominador sería 2. Luego, divido 2 entre 2, que es el denominador de la primera fracción, resulta 1 y lo multiplico por “a” menos “b”. Ah, aquí sí sé, profe Viète, que cualquier cantidad multiplicada por 1 me da la misma cantidad y hasta sé que es porque el 1 es el elemento neutro multiplicativo.
Viète:
Perfecto, pero no te pierdas.
Alumno:
Sí, decía que multiplicó por 1 y me vuelve a dar “a” menos “b” de la primera fracción. Luego, divido 2, que es el común denominador, entre 1 que es el denominador de la segunda fracción, y resulta 2, pero… ¿Cuánto es 2 por “b”?
Viète:
2 por “b” se puede escribir 2 “b”, y entonces quedaría “a” menos “b”, más 2 “b”, entre 2. Puedes reducir los términos semejantes con “b”, pero primero acomoda la fracción para que se entienda mejor, pon “a” más 2 “b”, menos “b”, entre 2. Recuerdas, ¿por qué se puede hacer eso?
Alumno:
Sí, porque en realidad no se altera nada de la expresión, ya que sólo se están reacomodando los términos.
Viète:
Claro, pero así quizá se pueda observar mejor que vamos a restar 2 “b” menos “b”, es decir, 2 “b” menos una “b” que es…
Alumno:
…pues una “b” o simplemente “b”, claro. Si tienes 2 “b” y restas una “b” el resultado es una “b” ¿no?
Viète:
Entonces, ¿cómo quedaría la fracción?
Alumno:
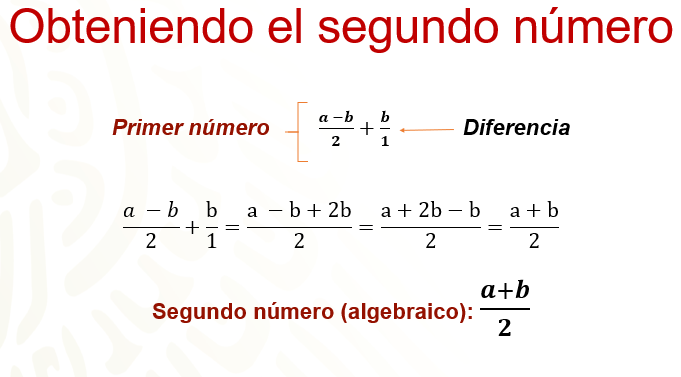
Quedaría, “a” más “b” entre 2. Y éste será el otro número simbólico que se busca. ¿Cierto?
Viète:
Sí, cierto. Finalmente, los números que se buscan son “a” menos “b” entre 2 y “a” más “b” entre “2”.

Alumno:
Me parece increíble que unas expresiones tan largas sean sólo dos números.
Viète:
Claro, así también le parecería al tal Diofanto, pero yo que inventé estas especies, digo, estos números algebraicos o simbólicos los veo como números. Sin embargo, los podemos convertir en los números específicos que tú conoces.
Alumno:
¿Cómo?
Viète:
Recuerda que al principio propusiste al número 100 como suma y al número 40 como diferencia de 2 números, y también recuerda que la tarea era mostrar que invariablemente se pueden encontrar esos números.
Alumno:
Y usted dice que esos números son “a” menos “b”, entre 2 y “a” más “b” entre 2…
Viète:
Sí, y también dije que la suma es “a” y la diferencia es “b”, entonces, si tú hubieras conocido los números simbólicos te habrías ahorrado todo tu procedimiento estilo Diofanto. Pero ahora que ya los conoces puedes comprobar la veracidad de mis números, sólo sustituye en estos números simbólicos los números que propusiste y listo.
Alumno:
¿Es decir, en lugar de “a” menos “b” entre 2, escribo: 100 menos 40 entre 2, y en lugar de “a” más “b”, entre 2, escribo 100 más 40, entre dos?
Viète:
En efecto, pero de uno por uno.
Alumno:
100 menos 40 es 60, entre 2 es, 30. El número menor. Ahora, 100 más 40 es 140 entre 2, resulta 70, el número mayor. ¡Zas! Ahora sí se lució, profe Viète.

Viète:
Claro que sí, pero debes comprobarlo con otros muchos números para que veas que funciona. Se te propone comprobar con: 280 y 45, 1360 y 850, o los que tú quieras.
Alumno:
¡Ahora sí me impresionó, profe Viète!
Viète:
A ver, ¿por qué mes estás llamando, profe Viète? Si soy uno de los más grandes matemáticos de la historia.
Alumno:
¡Lo siento, maestro, señor, doctor François Viète! Muchas gracias por ayudarme con mi tarea.
Viète:
No me des las gracias, no hemos terminado.
Alumno:
¡Ah no! ¿Qué falta?
Viète:
¡Que me pagues por la asesoría, jovencito! Son 200 francos porque yo no cobro en pesos mexicanos.
No te lo creas. Sólo bromeo, fue un placer haberte ayudado, jovencito, y, sobre todo, espero que hayas conocido más de mi vida y mis aportaciones matemáticas en la historia.
Después de haber visto esta ejemplificación, se espera que hayas sobre el matemático Viète y sus aportaciones a las matemáticas.
El reto de hoy:
Resuelve los ejercicios relacionados con el tema, en donde se te pide comprobar con: 280 y 45, 1360 y 850, o los números que tú quieras.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion