Fracciones decimales y no decimales
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Fracciones decimales y no decimales
Aprendizaje esperado: convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones no decimales usando la notación decimal. Ordena fracciones y números decimales.
Énfasis: identificar los tipos de fracciones y decimales.
¿Qué vamos a aprender?
Identificarás los tipos de fracciones y decimales. Recordarás lo que aprendiste en la sesión anterior sobre la definición de fracciones, las partes de las fracciones y su conversión a decimales.
¿Qué hacemos?
Encontrarás, en nuestro día a día, muchos ejemplos de los diferentes tipos de fracciones, ya que, no importando el contexto, las fracciones se usan en todo lugar.
Por ejemplo: las personas que trabajan en la plomería o construcción, al comprar tubo lo hacen por medidas como una pulgada, media pulgada o tres cuartos de pulgada; o también en la cocina, como lo viste en la clase anterior, al preparar alguna receta puedes encontrarte medidas de los ingredientes expresadas en fracciones o en decimales, como 1.5 kg de arroz, o medio kg de carne. Todos los días, al decir la hora o referirnos al tiempo, generalmente usamos expresiones como “media hora”, “un cuarto de hora” o “tres cuartos de hora”. Pero te has preguntado: ¿qué significa esta manera de medir el tiempo?
Es claro que las fracciones nos acompañan en nuestro día a día. Pero ¿sabías que existen diferentes tipos de fracciones y de números decimales? Cada una con sus características y cualidades propias. Para ilustrarlo mejor observa el siguiente video del minuto 00:21 al 02:01:
Tipos de fracciones y decimales
Hasta el momento has revisado 3 tipos de fracciones: las fracciones unitarias y las fracciones propias e impropias, cuyo valor puede ser representado utilizando figuras. Veamos qué sucede con la ubicación de las mismas en la recta numérica.
Recuerda que la recta numérica es una línea que contiene a todos los números reales.
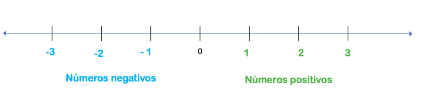
Cada segmento vertical en el esquema de la recta numérica representa un entero, aquí tienes tres hacia el lado derecho y tres hacia el lado izquierdo del cero. La fracción unitaria un tercio la localizaremos dividiendo el primer entero positivo en 3 partes iguales como se observa en seguida.

Posteriormente podemos ubicar la fracción un tercio de este modo.
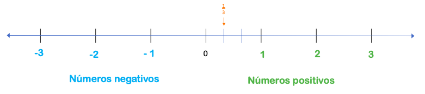
Es posible ubicar también dos tercios.
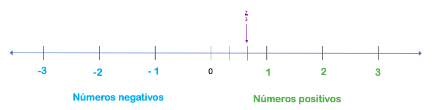
Y por supuesto también tres tercios, fracción que es equivalente o lo mismo que un entero y puede ser llamada fracción entera, ya que, si dividen el numerador entre el denominador, obtendrán como resultado una unidad.

¿Puedes mencionar otras fracciones enteras?
Ahora localicemos una fracción unitaria en nuestra recta numérica. Por ejemplo, un sexto, para ello tenemos que dividir nuestro primer entero positivo, en este caso, en sextos de la siguiente manera:

La fracción un sexto se localiza justo aquí.
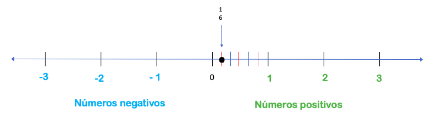
Por otro lado, la fracción unitaria un sexto negativo, la ubicamos a la misma distancia del cero, pero del lado contrario, el de los números negativos.

También debes recordar que al hablar de fracción unitaria nos referimos a que en el numerador el valor siempre es uno. Estas a su vez forman parte de las fracciones propias, en las que su numerador es menor que el denominador, por ejemplo, la fracción propia dos tercios que utilizamos anteriormente.
Observa que ninguna de las fracciones que mencionamos sobrepasa la unidad. Ten presente que a las fracciones cuyo valor absoluto es mayor al entero se les conoce como fracciones impropias, por ejemplo, cuatro tercios, ubiquémoslo en la recta numérica.

Otro ejemplo de fracción impropia es ocho sextos, una de tantas formas para poder ubicarla es continuar dividiendo el siguiente entero de nuestra recta numérica, primero en tercios.

Y luego en sextos, es decir, cada entero se divide en seis partes iguales.

La fracción ocho sextos se ubica contando las partes a partir del cero, contamos un sexto, dos sextos, tres sextos, y así sucesivamente hasta llegar a ocho sextos.
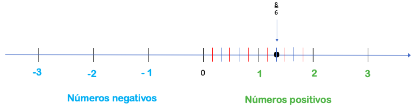
Así respondemos a la pregunta ¿Cuál es la relación entre estas fracciones respecto a un número entero?
La respuesta es que las fracciones propias son menores a un entero.

Y las impropias siempre serán mayores a la unidad, o bien mayores a un entero, como se ilustra en la imagen.
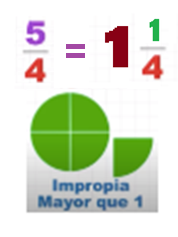
La fracción un entero un cuarto recibe el nombre de número mixto, por incluir una parte entera y una fraccionaria. En el ejemplo anterior, observa que cinco cuartos es una fracción equivalente a 1 entero y un cuarto.
Un ejemplo común es cuando vas a la tienda a comprar 1 kg y medio kilogramo de arroz.

¿Qué pasa cuando el numerador y denominador son iguales?
A las fracciones como tres tercios o cinco quintos se les denomina fracciones enteras, y siempre dan como resultado la unidad.

Anota 5 ejemplos de fracciones enteras en tu cuaderno y represéntalas de manera gráfica. ¡Usa tu creatividad! Utiliza ejemplos sencillos como dos medios, cinco quintos o bien ocho octavos, para crear divertidos diseños. Usando colores diferentes, papel de distintos tipos y los elementos de reciclaje que tengas a tu alcance para lograrlo. Aquí te presentamos un modelo.

Ahora que hablamos de fracciones enteras. Te has preguntado: ¿Cuál será la fracción unitaria más grande que existe?
Recuerda que para que sea unitaria debe tener uno en el numerador.
¿Cuál será la fracción propia más grande?
Recuerda que en las fracciones propias el numerador siempre es menor que el denominador. Así que, si se divide en 10, la fracción propia más grande ¿sería nueve décimos?
¿Cuál será la fracción impropia más pequeña?
Para profundizar en el tema observa el siguiente video del minuto 00:21 a 02:01:
De fracción común a fracción decimal
Ahora ya sabes que las fracciones con una potencia de 10 en el numerador reciben el nombre de fracciones decimales.
¿Recuerdas algún momento de tu vida cotidiana en el que hayas utilizado una fracción decimal? Por ejemplo: cuando hablas de 50 centavos con tus amigos o familiares, y tomas como referencia 1 peso, estás refiriéndote a la fracción decimal cinco décimos y a su fracción unitaria equivalente un medio ya que 50 centavos representan la mitad de un peso.
Te invitamos a tomar tu cuaderno ¿Puedes ubicar en la recta numérica la fracción decimal cinco décimos? Para eso traza primero tu recta numérica, posteriormente divide cada entero en tantas partes como sea necesario y ¡ubica la fracción!
Observa otro video del minuto 02:32 a 03:00 para ampliar los conocimientos en cuanto a números decimales.
Tipos de fracciones y decimales
https://www.youtube.com/watch?v=CDnq-63F_Tg&feature=youtu.be
Las fracciones que estudiaste anteriormente pueden ser representadas como un número decimal. Como viste, los números decimales se escriben y leen de diferentes formas.
Veamos más ejemplos con la recta numérica.
Si nuestra fracción decimal es seis décimos, necesitamos dividir el primer entero en 10 partes iguales tal y como se muestra, y la ubicamos de la siguiente manera.

Un décimo, dos décimos, tres décimos, cuatro décimos, cinco décimos, seis décimos.

¿Qué pasaría si la fracción fuera setenta y cinco centésimos?, ¿cómo lo resolverías?
En este caso significa que la recta numérica en lugar de estar dividida en 10 partes iguales del 0 al 1, estaría dividida en 100 partes y buscaríamos nuestra fracción decimal en el número 0.75 centésimos, que también sería igual a tres cuartos

¿Y si mi fracción decimal es (veinticinco décimos)? ¿Dónde estaría ubicada?
Veinticinco décimos, significa que tienes 2 enteros y cinco décimos, por lo tanto, estaría ubicada de la siguiente manera.
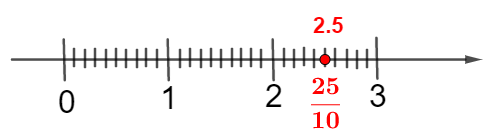
Existen otros dos tipos de decimales: los decimales finitos y los decimales infinitos.
Imagina que un número decimal no tenga fin, sería kilométrico, como de aquí al sol dos vueltas y de regreso, y podría seguir.
Es como el número “Pi”, que puedes redondear a 3.1416 diezmilésimos, pero al presionar el símbolo en una calculadora nos mostraría tantos dígitos que quepan en la pantalla, pero tendría infinidad de números después del punto decimal, este es un buen ejemplo de un número decimal infinito.
En cambio, un número finito puede ser un medio, cinco sobre diez o 0.5 décimos Los cuales representan el mismo valor, como en el ejemplo de los centavos.
Recapitulando:
- Decimal finito o exacto: es aquel que tiene una cantidad determinada de decimales.
- Decimal infinito: es aquel que tiene una cantidad infinita de decimales.
Por ejemplo:
Pi, que es un número muy complejo y es importante saber que a este tipo de número se le conoce como número irracional, porque sus decimales no siguen un orden definido.
Pi= 3.14159265358979…
Dentro de los decimales infinitos también encontramos los decimales periódicos. Para ejemplificar la diferencia entre decimal finito y decimal periódico observa el siguiente video
Tipos de fracciones y decimales
Sección de video: 03:00 a 04:
https://www.youtube.com/watch?v=CDnq-63F_Tg&feature=youtu.be
Convertiremos a número decimal, cada una de las siguientes fracciones que ilustran a los decimales periódicos. Comencemos con:

0.555555555555555555555555555555555…
Observen que en esta primera fracción el número 5 aparece como un valor decimal y se repite de manera infinita, por lo tanto, es un decimal periódico.
Ahora la fracción:

0.727277272727272
En el segundo caso son dos cifras después del punto decimal las que se repiten en el periodo, el número 72.
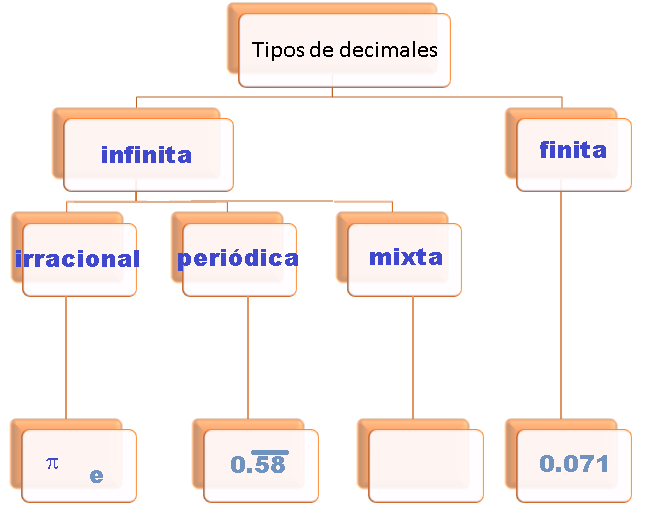
Finita: quiere decir que tiene una cantidad definida de decimales.
Infinita: que tiene una cantidad infinita de decimales, que a su vez podemos dividir en dos diferentes: irracionales y periódicas.
La característica de los decimales mixtos es que tienen decimales que no se repiten, pero sí hay una parte que se repite periódicamente.
Por ejemplo: cero punto setenta y dos centésimos con periodo en el dos (0.72…) que es equivalente a trece dieciochoavos; o también: cero punto veintiséis centésimos con periodo en el 6 (0.26…) que es equivalente a cuatro quinceavos
0.72222222... y 0.26666…
Es amplia la información relacionada con el tema. Cuando vayas de compras, cuando cocines, cuando vean la hora, entre otras cosas, puedes identificar los tipos de fracciones y decimales que utilizas.
Ahora podemos responder las preguntas planteadas.
¿Cuál es la fracción unitaria más grande?
La respuesta correcta es un medio que representa 0.5 décimos en número decimal.
¿Cuál es la fracción propia más grande?
Un ejemplo es nueve sobre diez cuya representación decimal es 0.9 decimos
En este caso siempre podremos encontrar una representación decimal más cercana a la unidad como por ejemplo 0.95 o bien 0.98
La última pregunta nos hace reflexionar sobre la fracción impropia más pequeña o más cercana a la unidad, tal vez pensaste en una fracción como cinco cuartos que es igual a 1.25 centésimos, pero si lo vemos como un número decimal podemos pensar en un número más cercano a la unidad como 1.1 décimo, que en fracción sería once sobre diez. De esta manera concluimos que al igual que en el caso anterior, siempre será posible encontrar una fracción impropia más cercana a la unidad.
El reto de hoy:
Revisa en tu libro de texto el tema “Identificación de fracciones y decimales” y realiza las actividades que ahí se sugieren.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion