Fracciones con dinero

Fracciones con dinero

Aprendizaje esperado: identificación de fracciones equivalentes al resolver problemas de reparto y medición.

Énfasis: establece relaciones de equivalencia entre dos o más fracciones al resolver problemas de reparto y de medición.

¿Qué vamos a aprender?

Resolverás problemas de reparto y medición utilizando las fracciones equivalentes.

¿Qué hacemos?

Lee y resuelve este problema de reparto. Pon mucha atención y, si es necesario, anota los datos en tu cuaderno.

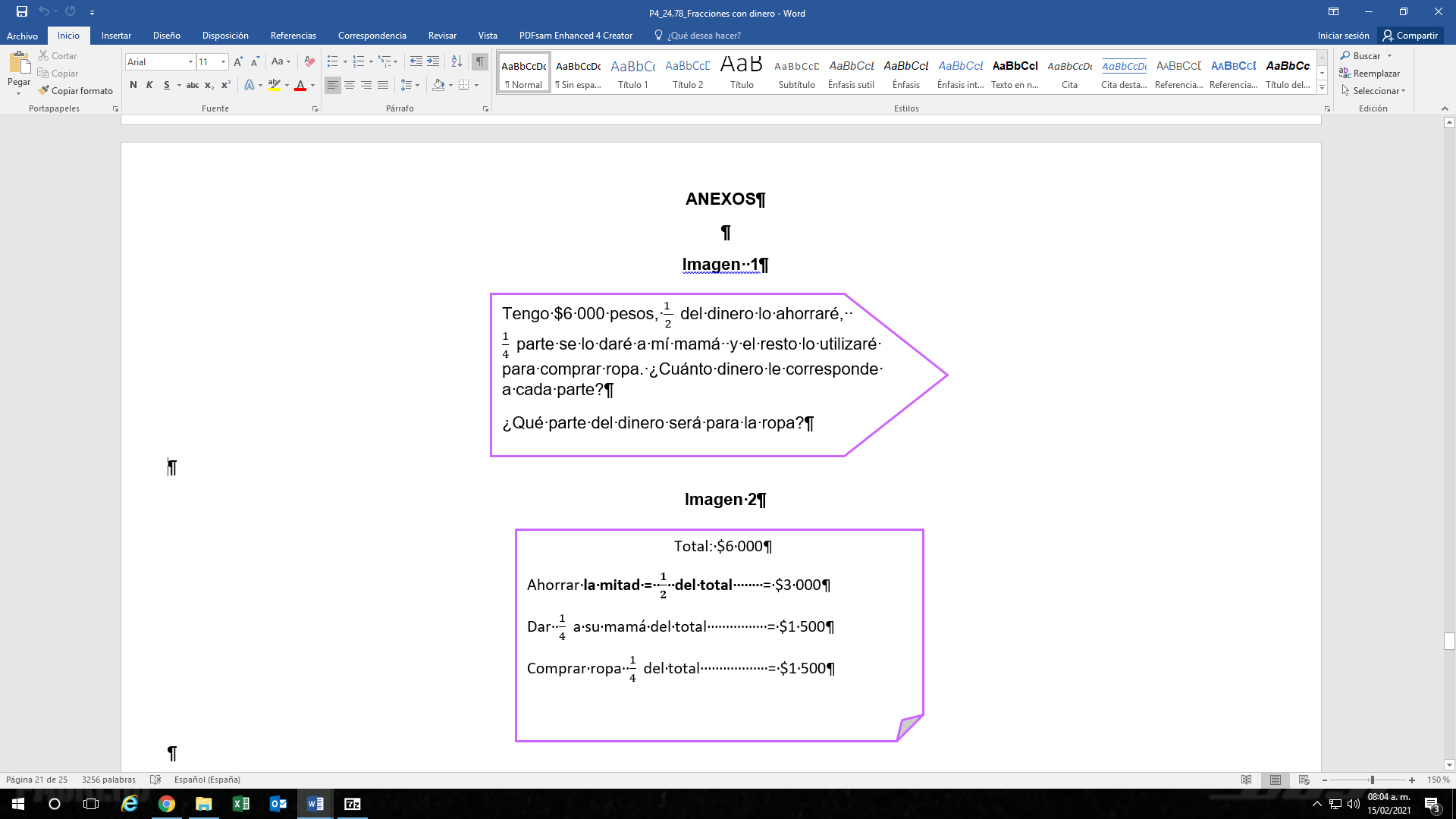
Tienes $6,000 pesos, la mitad del dinero, que es lo mismo que un medio, ahorrarás, una cuarta parte, que es lo mismo que escribir ¼, se lo darás a tú mamá y el resto lo utilizarás para comprar ropa. ¿Cuánto dinero le corresponde a cada parte? ¿Qué parte del dinero será para la ropa?

Recuerda que el total son $6,000 pesos, ¿Cuánto quieres ahorrar? Si es la mitad y equivale a escribir

La mitad serían $3,000 pesos, es como si hubiera divido entre dos. Ahora como ya sabes que vas a buscar cuánto dinero es la cuarta parte. ¿Qué se te ocurre? piensa, si de $6,000 son $3,000, ¿Cuánto sería un cuarto? ¿Cuánto es ¼ de 6000?

Primero, $3,000 pesos representan ½ del entero, se puede dividir a la mitad los $3,000 para que se conviertan en cuartos, si divides los $3,000 entre 2 serían $1,500 pesos, recuerda que en las sesiones anteriores aprendiste que ½ es equivalente a 2/4.

Entonces, tienes que $1,500 pesos es una cuarta parte de $6 000. ¿De qué otra manera puedes resolver este problema?

Puedes dividir los $6,000 pesos entre 4, de esta manera se divide el entero en 4 partes, ¿Cuál sería la respuesta? Si se tiene que repartir 6000 en 4.

La respuesta también es $1,500

$1,500 + $1,500 + $1,500 + $1,500 = $6,000

En la primera línea puedes observar que cuatro cuartos es igual a un entero y en la segunda línea son los mismos cuatro cuartos, pero representados con los datos del problema, cada cuarto equivale a 1 500, entonces cuatro veces 1 500 es igual a 6 000.

Entonces de los $6,000, la mitad o un medio que quiere ahorrar corresponde a $3,000 pesos y un cuarto que le darás a mamá serían $1,500, ¿Cuánto te quedó entonces para tus gastos?

¿Recuerdas otra fracción equivalente a ¼? Observa todo lo que has descubierto de este problema.

Ahora, vas a resolver el desafío matemático número 50, que está en la página 97 de tu libro de texto.

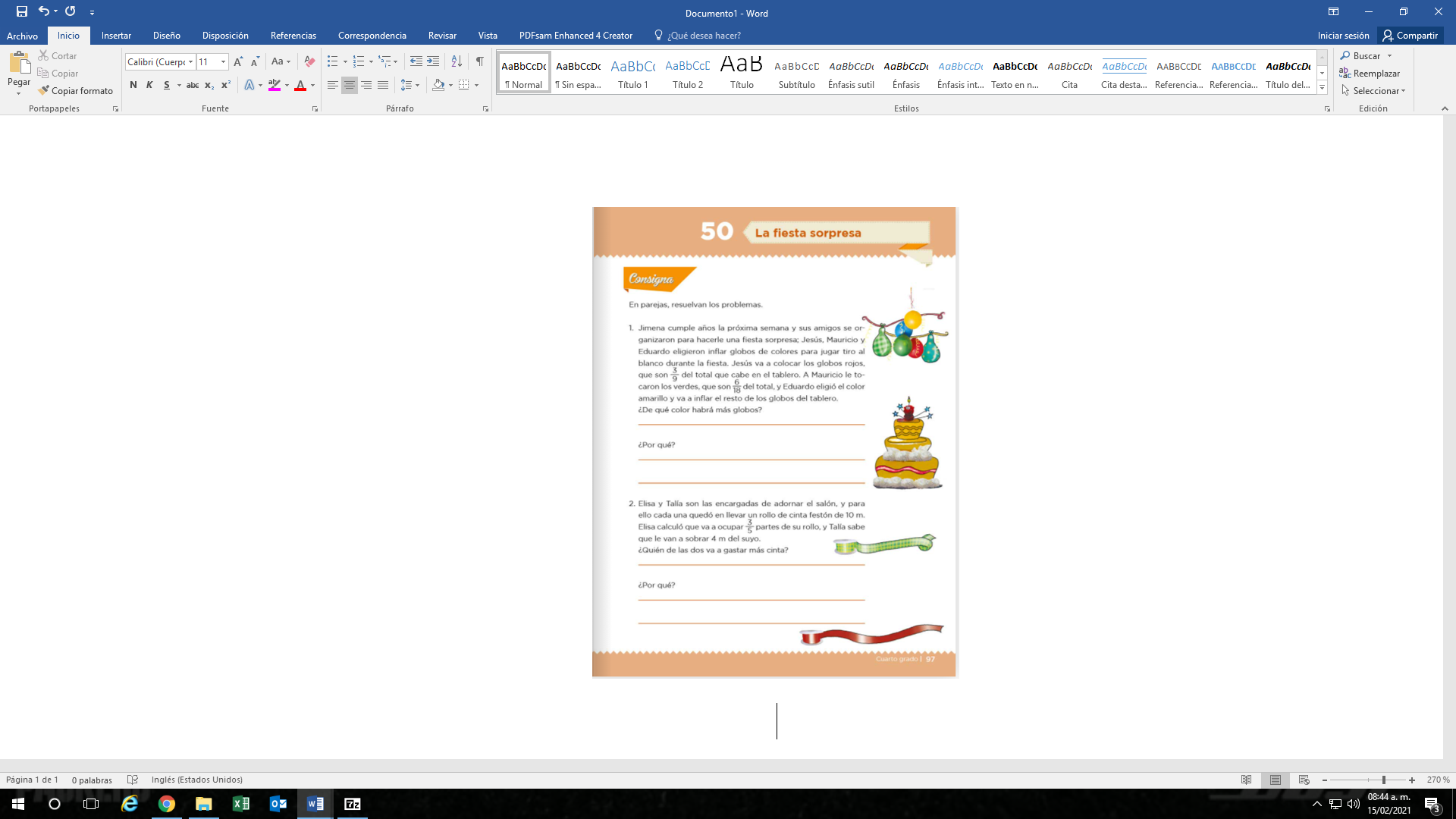
https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/97

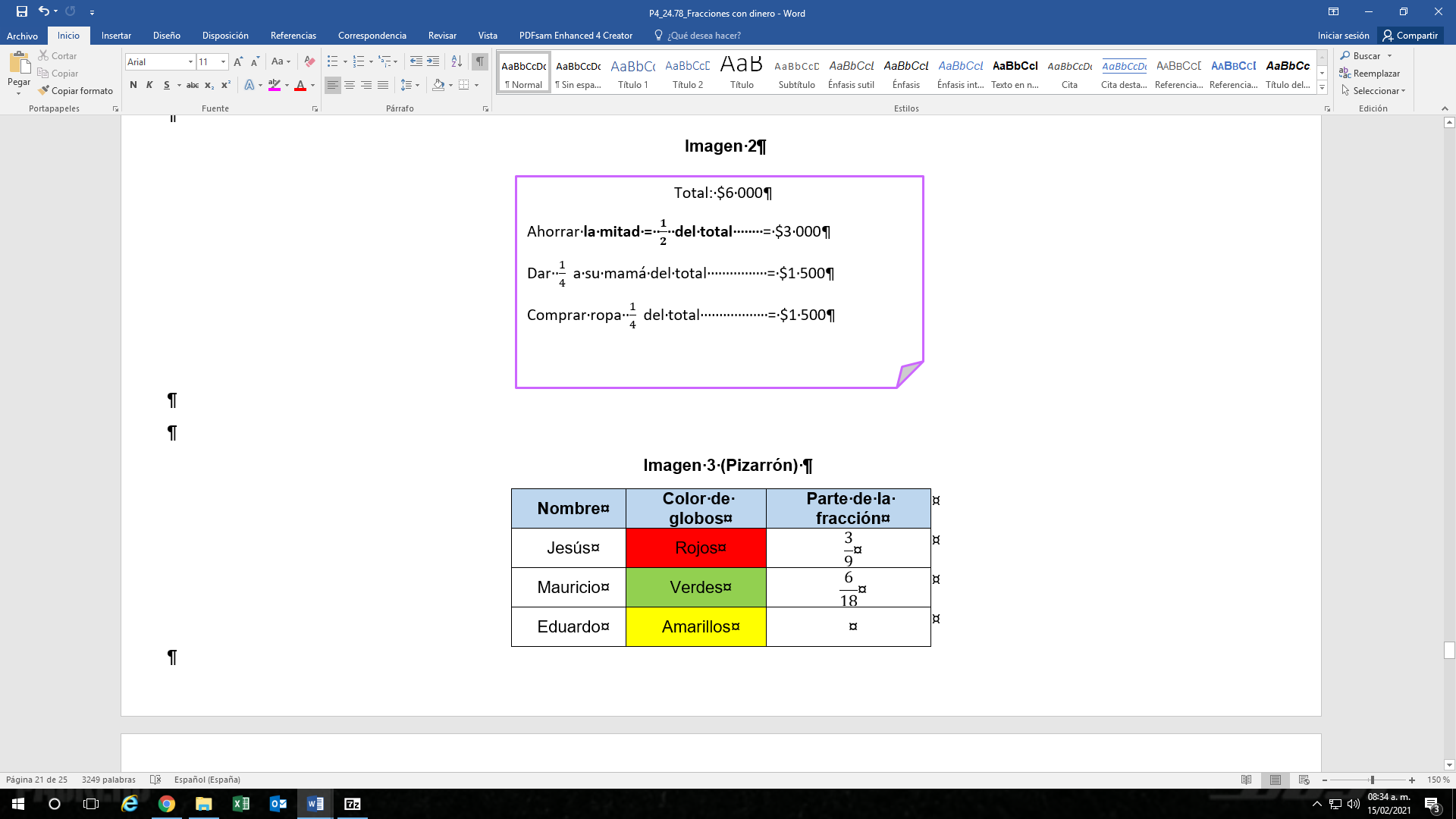
Jimena cumple años la próxima semana y sus amigos se organizaron para hacerle una fiesta sorpresa: Jesús, Mauricio y Eduardo eligieron inflar globos de colores para jugar tiro al blanco durante la fiesta. Jesús va a colocar los globos rojos, que son 3/9 del total que cabe en el tablero. A Mauricio le tocaron los verdes, que son 6/18 del total, y Eduardo eligió el color amarillo y va a inflar el resto de los globos del tablero. ¿De qué color habrá más globos?

Tienes los siguientes datos:

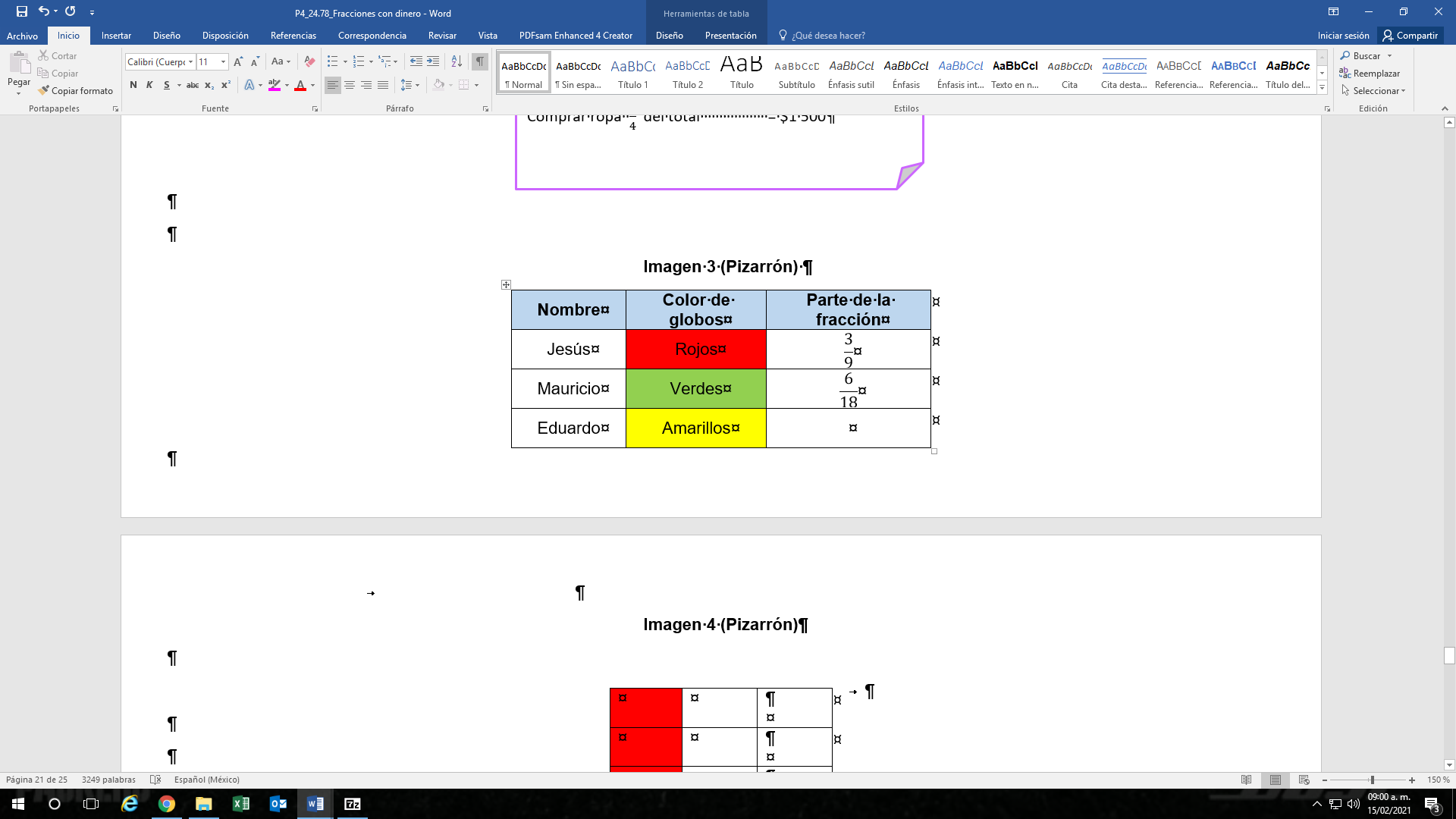
Jesús, cubrirá tres novenos de globos rojos. Se deben iluminar las 3/9 partes de color rojo.

Estás utilizando un 1/3 del tablero.

Ahora hay que representar los globos verdes que corresponden 6/18. Para hacerlo divide todo en 18 partes iguales y toma 6/18. Para los globos verdes.

Esto te dice que si sumas 3/9 más 6/18 es igual a 2/3 de la pieza, aquí hay otra equivalencia. Y queda 1/3 de pieza.

¿Qué pasa con este último tercio? ¿Ya lo sabes? Si no, lee nuevamente el desafío.

Sí, se pinta de color amarillo, éstos son lo que va a inflar Eduardo. Por lo tanto, el tablero queda de la siguiente manera:

¿De qué color hubo más globos? Los tres inflaron la misma cantidad de globos, así que hubo la misma cantidad de globos, entonces puedes concluir que estas fracciones son equivalentes.

Ahora continuarás con otro problema, para que te quede más claro utilizarás algunos materiales para que lo puedas entender mejor.

Lee el problema número 2 de la consigna:

Elisa y Talía son las encargadas de adornar el salón, y para ello cada una quedó en llevar un rollo de cinta festón de 10 m. Elisa calculó que va a ocupar 3/5 partes de su rollo, y Talía sabe que le van a sobrar 4 m. del suyo. ¿Quién de las dos va a gastar más cinta?

Fíjate bien, Elisa y Talía tiene cada una un rollo de cinta festón. Elisa dice que sólo va a ocupar 3/5 partes de su rollo, por otra parte, Talía sabe que le sobrarán 4 m de su rollo. ¿Cuántos metros usará cada una? ¿Qué se te ocurre hacer para saberlo?

Primero divide el festón de Elisa, en 5 partes y de ahí toma 3/5 partes. Después divide el festón de Talía de metro en metro y quita los 4 metros que le sobran. Así sabrás cuánto usará cada una.

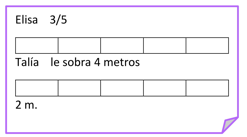
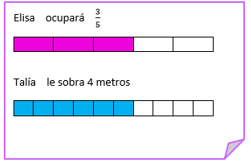
Aquí están los tres quintos de festón que ocupará Elisa y aquí ya se quitaron los 4 m de listón que le sobran a Talía. ¿Podrías decir qué fracción del festón usó Talía?

Así es, ocupó seis décimos, porque se dividieron los 10 metros del rollo en tiras de un metro.

Y así puedes ver que Elisa y Talía ocuparán la misma cantidad de festón, entonces, ¿Qué podrías decir acerca de las dos fracciones, 3/5 y 6/10?

Estas dos fracciones representan la misma cantidad y por tanto se les conoce como fracciones equivalentes.

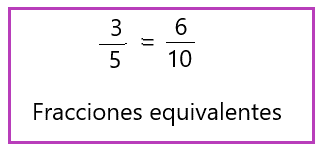
Recuerda que puedes encontrar fracciones escritas con diferente numerador y denominador, pero si representan la misma parte del entero, entonces son fracciones equivalentes.

Las fracciones no sólo se usan para partir un pastel, una galleta o una gelatina, sino que también las puedes usar para partir una cantidad, como ahora que fraccionaste una cantidad de dinero, y también en otras muchas cosas de la vida cotidiana.

Sigue practicando este tema, si te es posible plática con tus compañeros de clase y maestro sobre las distintas estrategias que utilizaron para resolver la consigna.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P4DMA.htm