Fracciones con dinero

Aprendizaje esperado: identifica de fracciones equivalentes al resolver problemas de reparto y medición .

Énfasis: establece relaciones de equivalencia entre dos o más fracciones al resolver problemas de reparto y de medición.

¿Qué vamos a aprender?

Resolverás problemas de reparto y medición utilizando las fracciones equivalentes.

¿Qué hacemos?

Lee y resuelve este problema de reparto. Pon mucha atención y, si es necesario, anota los datos en tu cuaderno.

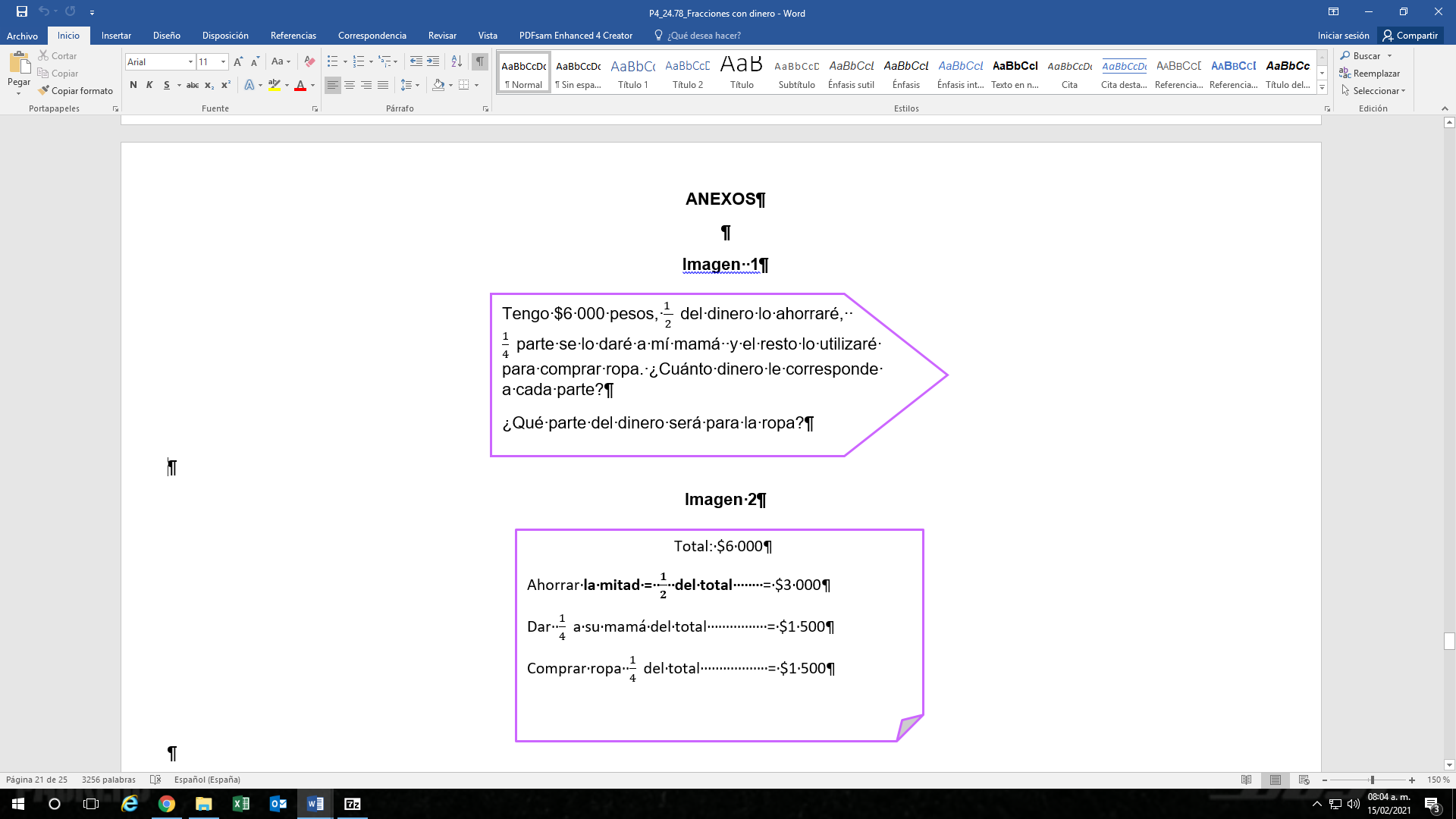
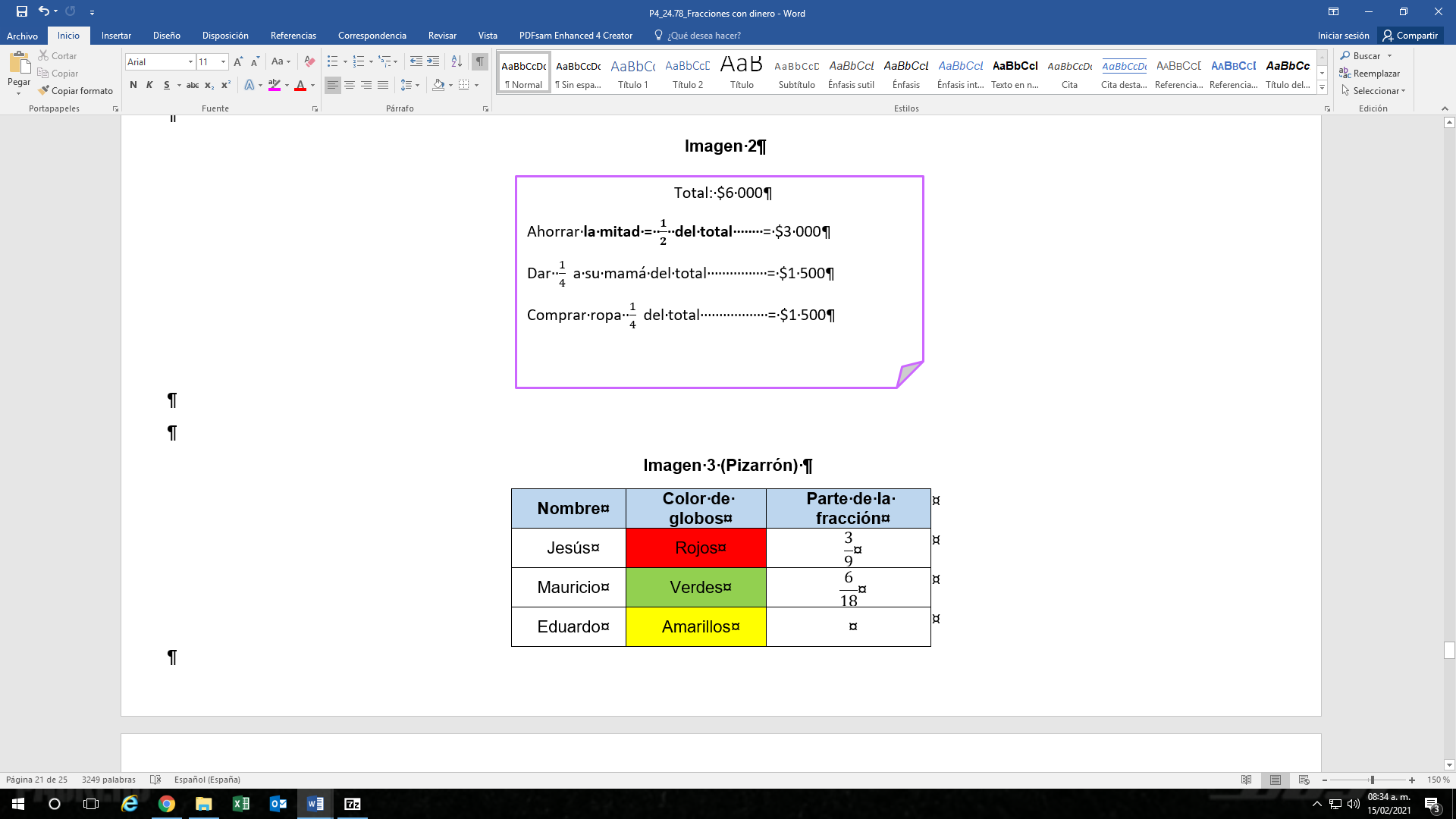
Tienes $6,000 pesos, la mitad del dinero, que es lo mismo que un medio, ahorrarás, una cuarta parte, que es lo mismo que escribir ¼, se lo darás a tú mamá y el resto lo utilizarás para comprar ropa. ¿Cuánto dinero le corresponde a cada parte? ¿Qué parte del dinero será para la ropa?

Recuerda que el total son $6,000 pesos, ¿Cuánto quieres ahorrar? Si es la mitad y equivale a escribir 1 2

La mitad serían $3,000 pesos, es como si hubiera divido entre dos. Ahora como ya sabes que 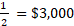1 2 =$3,000 vas a buscar cuánto dinero es la cuarta parte. ¿Qué se te ocurre? piensa, si 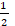1 2 de $6,000 son $3,000, ¿Cuánto sería un cuarto? ¿Cuánto es ¼ de 6000?

Primero, $3,000 pesos representan ½ del entero, se puede dividir a la mitad los $3,000 para que se conviertan en cuartos, si divides los $3,000 entre 2 serían $1,500 pesos, recuerda que en las sesiones anteriores aprendiste que ½ es equivalente a 2/4.

Entonces, tienes que $1,500 pesos es una cuarta parte de $6 000. ¿De qué otra manera puedes resolver este problema?

Puedes dividir los $6,000 pesos entre 4, de esta manera se divide el entero en 4 partes, ¿Cuál sería la respuesta? Si se tiene que repartir 6000 en 4.

La respuesta también es $1,500

1 4 + 1 4 + 1 4 + 1 4 =1 entero

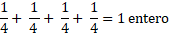
$1,500 + $1,500 + $1,500 + $1,500 = $6,000

En la primera línea puedes observar que cuatro cuartos es igual a un entero y en la segunda línea son los mismos cuatro cuartos, pero representados con los datos del problema, cada cuarto equivale a 1 500, entonces cuatro veces 1 500 es igual a 6 000.

Entonces de los $6,000, la mitad o un medio que quiere ahorrar corresponde a $3,000 pesos y un cuarto que le darás a mamá serían $1,500, ¿Cuánto te quedó entonces para tus gastos?

¿Recuerdas otra fracción equivalente a ¼? Observa todo lo que has descubierto de este problema.

Ahora, vas a resolver el desafío matemático número 50, que está en la página 97 de tu libro de texto.

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/97

Jimena cumple años la próxima semana y sus amigos se organizaron para hacerle una fiesta sorpresa: Jesús, Mauricio y Eduardo eligieron inflar globos de colores para jugar tiro al blanco durante la fiesta. Jesús va a colocar los globos rojos, que son 3/9 del total que cabe en el tablero. A Mauricio le tocaron los verdes, que son 6/18 del total, y Eduardo eligió el color amarillo y va a inflar el resto de los globos del tablero. ¿De qué color habrá más globos?

Tienes los siguientes datos:

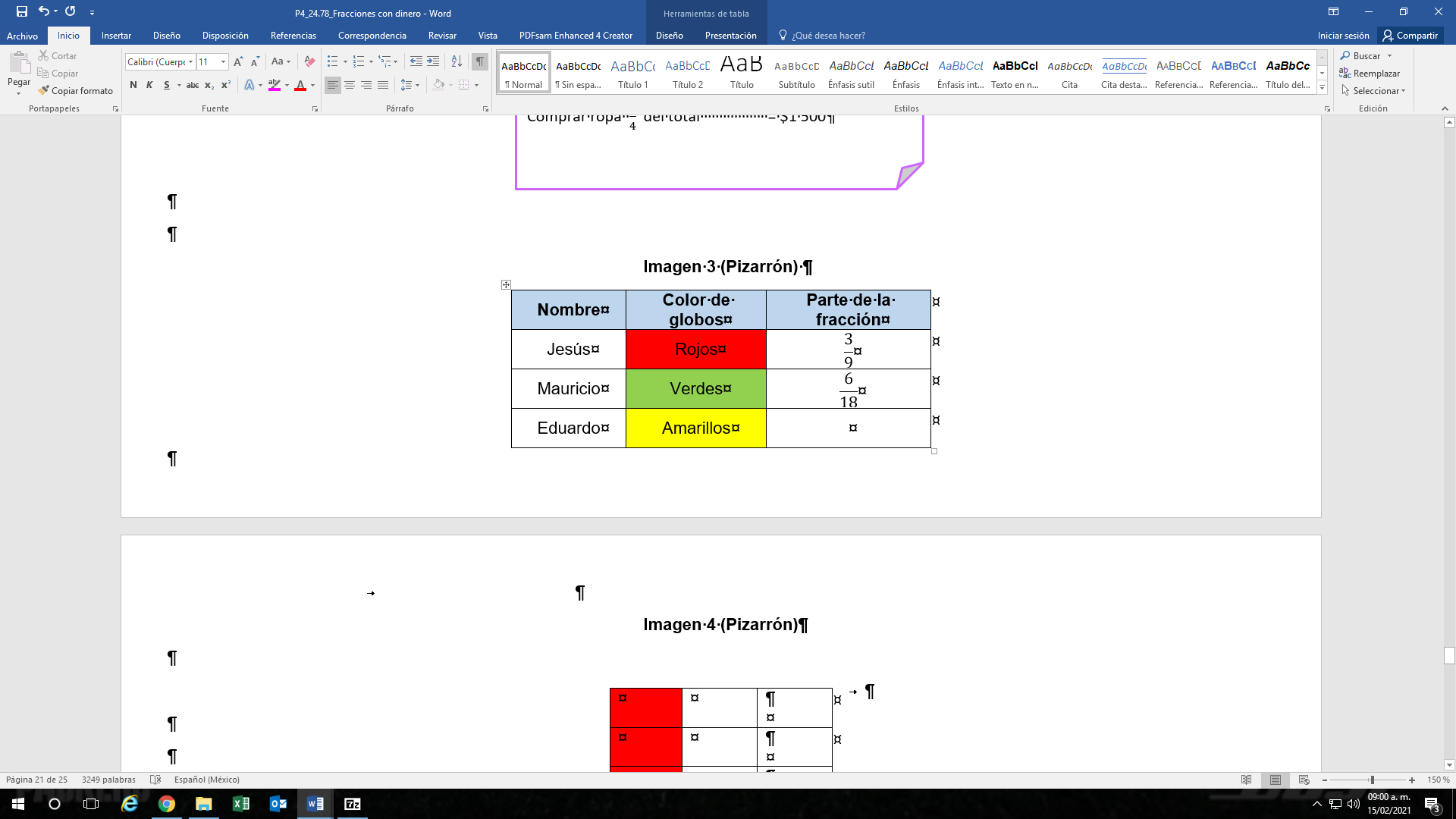
Jesús, cubrirá tres novenos de globos rojos. Se deben iluminar las 3/9 partes de color rojo.

Estás utilizando un 1/3 del tablero.

Ahora hay que representar los globos verdes que corresponden 6/18. Para hacerlo divide todo en 18 partes iguales y toma 6/18. Para los globos verdes.

Esto te dice que si sumas 3/9 más 6/18 es igual a 2/3 de la pieza, aquí hay otra equivalencia. Y queda 1/3 de pieza.

¿Qué pasa con este último tercio? ¿Ya lo sabes? Si no, lee nuevamente el desafío.

Sí, se pinta de color amarillo, éstos son lo que va a inflar Eduardo. Por lo tanto, el tablero queda de la siguiente manera:

¿De qué color hubo más globos? Los tres inflaron la misma cantidad de globos, así que hubo la misma cantidad de globos, entonces puedes concluir que estas fracciones son equivalentes.

3 9	6 18	1 3

Ahora continuarás con otro problema, para que te quede más claro utilizarás algunos materiales para que lo puedas entender mejor.

Lee el problema número 2 de la consigna:

Elisa y Talía son las encargadas de adornar el salón, y para ello cada una quedó en llevar un rollo de cinta festón de 10 m. Elisa calculó que va a ocupar 3/5 partes de su rollo, y Talía sabe que le van a sobrar 4 m. del suyo. ¿Quién de las dos va a gastar más cinta?

Fíjate bien, Elisa y Talía tiene cada una un rollo de cinta festón. Elisa dice que sólo va a ocupar 3/5 partes de su rollo, por otra parte, Talía sabe que le sobrarán 4 m de su rollo. ¿Cuántos metros usará cada una? ¿Qué se te ocurre hacer para saberlo?

Primero divide el festón de Elisa, en 5 partes y de ahí toma 3/5 partes. Después divide el festón de Talía de metro en metro y quita los 4 metros que le sobran. Así sabrás cuánto usará cada una.

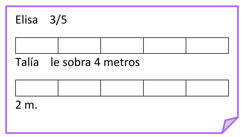
Aquí están los tres quintos de festón que ocupará Elisa y aquí ya se quitaron los 4 m de listón que le sobran a Talía. ¿Podrías decir qué fracción del festón usó Talía?

Así es, ocupó seis décimos, porque se dividieron los 10 metros del rollo en tiras de un metro.

Y así puedes ver que Elisa y Talía ocuparán la misma cantidad de festón, entonces, ¿Qué podrías decir acerca de las dos fracciones, 3/5 y 6/10?

Estas dos fracciones representan la misma cantidad y por tanto se les conoce como fracciones equivalentes.

Recuerda que puedes encontrar fracciones escritas con diferente numerador y denominador, pero si representan la misma parte del entero, entonces son fracciones equivalentes.

Las fracciones no sólo se usan para partir un pastel, una galleta o una gelatina, sino que también las puedes usar para partir una cantidad, como ahora que fraccionaste una cantidad de dinero, y también en otras muchas cosas de la vida cotidiana.

Sigue practicando este tema, si te es posible plática con tus compañeros de clase y maestro sobre las distintas estrategias que utilizaron para resolver la consigna.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí