Formulación de ecuaciones lineales
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42
Formulación de ecuaciones lineales
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: resolver problemas mediante la formulación y solución de ecuaciones lineales.
¿Qué vamos a aprender?
Resolverás problemas mediante la formulación y solución algebraica de ecuaciones lineales.
¿Qué hacemos?
Las ecuaciones han sido parte de las sociedades civilizadas, desde la antigüedad debido al creciente cambio de conocimientos matemáticos; por ejemplo, los antiguos egipcios que desarrollaron conocimientos matemáticos y científicos para hacer frente a las necesidades de la vida cotidiana y del Estado faraónico. Los egipcios utilizaron las matemáticas como herramienta para resolver problemas prácticos, mencionamos algunos de ellos: medir las parcelas de cultivo, contabilizar el producto de las cosechas, el cobro de los impuestos o las ofrendas a los templos, calcular la altura de alguna pirámide eran labores que requerían todo tipo de operaciones matemáticas, desde las más simples hasta las más complejas. Varias de las operaciones que se generaron en ese entonces, continúan vigentes hasta el día de hoy, en diferentes disciplinas y mediante el apoyo de las distintas áreas de las matemáticas. Un claro ejemplo, del uso matemático es la siguiente ecuación: ¿Cuánto vale el montón de vasijas, si el montón y un séptimo del montón es igual a 24?
Este es un problema algebraico que se encuentra planteado y resuelto en un papiro egipcio desde hace 3,670 años es decir del año 1,650 antes de nuestra era. En la actualidad lo resolveríamos por medio de un método diferente y mediante una ecuación, pero para llegar a este análisis, el camino ha sido complejo en la búsqueda de conocimiento y esto es gracias a los primeros matemáticos que desarrollaron métodos sistemáticos para resolver ecuaciones, nos referimos a los matemáticos árabes. En aquel entonces, a la incógnita la llamaban “la cosa”, algo parecido a lo de “el montón” egipcio.
Ya has aprendido a traducir del lenguaje común a lenguaje algebraico, con esto podemos construir una ecuación y dar solución al problema. La cosa, la representaremos mediante una incógnita. En la imagen se observa el problema que es un montón de vasijas más un séptimo del montón es igual a 24, si lo traducimos al lenguaje algebraico, el montón de vasijas sería “la cosa” y lo representamos con una incógnita, en este caso “x” más un séptimo del montón que representamos como “x” séptimos o “x” sobre 7; por lo que resulta la ecuación “x” + “x” séptimos es = 24.
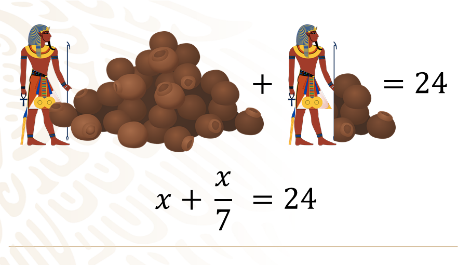
Por medio de la propiedad uniforme de la igualdad, multiplicaremos por 7 ambos miembros de la ecuación, de forma que podamos obtener una ecuación equivalente para trabajar con valores enteros, resulta:
7 (x+x/7)= 7 (24)
Por medio de la propiedad distributiva de la igualdad eliminaremos los paréntesis de ambos miembros.
7x + x = 168
Reduciendo términos semejantes podemos sumar.
8x = 168
Ahora para despejar a “x” dividimos a ambos miembros entre 8.
X= 168/8
X= 21
Para comprobar el resultado, sustituimos el valor encontrado de x en la ecuación.
X + x/7 = 24
21 + 21/7 = 24
21 + 3 = 24
24 = 24
Esto significa que el montón de vasijas es 21 lo cual se adiciona con un tercio de ese montón, lo cual es 3.
Al inicio de la sesión leíste que los egipcios medían sus parcelas, que son extensiones de terrenos que pueden ser destinadas para sembrar o para construir. Así que plantamos la siguiente situación: Un grupo de campesinos disponía de una parcela rectangular que era 18 metros más larga que ancha, y tenía una valla de 156 metros. ¿Cuáles son las dimensiones de la parcela?
Para poder resolver esta situación primero debemos traducirla a lenguaje algebraico quedando de la siguiente manera: En la imagen puedes observar un rectángulo en donde la medida del ancho es desconocida, es decir, una incógnita, por lo tanto, la podemos representar con una literal en este caso “p” y la medida del largo es 18 metros más que el ancho por lo tanto, lo podemos representar como “p” + 18 y tiene una valla que mide 156 metros que representa el contorno de la parcela, es decir, el perímetro.
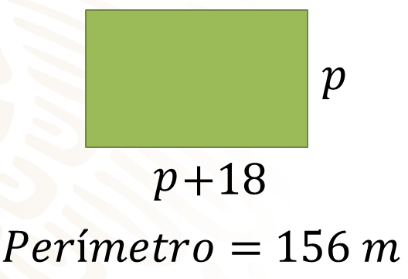
Como ya tenemos la traducción de la situación a lenguaje algebraico, ahora podemos construir la ecuación y darle solución. Sabemos que el perímetro es igual a la suma de los lados del rectángulo, entonces nos queda que: 2 veces “p” más 2 veces “p” más 18 es igual a 156 resultando de la siguiente manera:
2p + 2 (p + 18) = 156
Por medio de la propiedad distributiva eliminaremos los paréntesis.
2p + 2p + 36 = 156
Por medio de la propiedad uniforme restaremos 36 a ambos miembros de la ecuación, resultando:
4p + 36 -36 = 120
Para despejar a “p” dividiremos a ambos miembros entre 4.
4p/4 = 120/4
P = 30
Ahora comprobémoslo mediante la sustitución del valor de “p” en la ecuación.
2p + 2 (p+18) = 156
2 (30) + 2 (30 + 18) = 156
60 + 2 ( 48) = 156
60 + 96 = 156
156 = 156
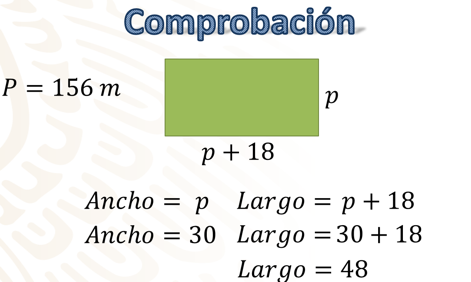
Con lo que acabamos de resolver las dimensiones de la parcela serían las siguientes: “p” que es el ancho y “p” más 18 que es el largo; sustituyendo a “p” para el ancho de la parcela, es igual a 30, mientras que el largo es “p” más 18, sustituyendo resulta 30 más 18 es igual a 48; por lo tanto, el largo de la parcela es de 48 metros y el ancho de 30 metros.
Los antiguos egipcios, a pesar de trabajar duramente, también aprovechaban el tiempo para divertirse. Tenían diferentes tipos de juguetes, no muy distintos a los nuestros, les gustaba jugar al aire libre y hacían competencias de tiro con arco.
Plantearemos una situación hipotética, con respecto a esas competencias, para desarrollar otro planteamiento: Un pueblo egipcio organizó una competencia de arco, tres cuartas partes de los jóvenes que había en el lugar se inscribieron y en el día de la competencia entraron 9 jóvenes más, lo que hizo un total de 84 competidores ¿Cuántos jóvenes había en ese pueblo?
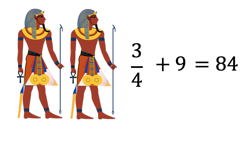
En este caso, usamos como literal para representar a la incógnita a “y” que corresponde al total de jóvenes que hay en el pueblo. La situación nos menciona que se inscribieron 3 cuartas partes de los jóvenes que representamos como tres cuartos de “y” y posteriormente entraron 9, así que sería más 9 teniendo un total de 84 competidores por lo tanto la ecuación que representa la situación es:
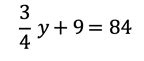
Por medio de la propiedad uniforme de la igualdad multiplicaremos por 4 a ambos miembros para obtener una ecuación equivalente para operar con números enteros.
4 ( ¾ y + 9) = 4 x 84
Por medio de la propiedad distributiva de la igualdad eliminaremos los paréntesis.
12/4 y + 36 = 336
3y + 36 = 336
Para resolverla, por medio de la propiedad uniforme restaremos 36 a ambos miembros.
3y + 36 – 36 = 336 – 36
3y = 300
Dividiendo entre 3 a ambos miembros de la ecuación.
3y/3 = 300/3
Y= 100
Comprobemos la solución en la ecuación.
¾ y + 9 = 84
¾ 100 + 9 = 84
300/4 + 9 = 84
75 + 9 = 84
84 = 84
Por lo tanto, ese pueblo egipcio tenía un total de 100 jóvenes.
El reto de hoy:
Como reto te proponemos que construyas la ecuación que represente la siguiente situación y des solución a la misma: Luis compró una bicicleta de 10 velocidades en 1,720 pesos. Si dio un pago inicial de 760 pesos y dio mensualidades de 240 pesos.
- ¿Cuántos meses tardó Luis en pagar la bicicleta?
- ¿Con qué ecuación modela el problema?
- ¿Cuál es la solución?
El procedimiento para resolver problemas de ecuaciones de primer grado es el siguiente:
- Identificar la incógnita del problema: Debemos saber qué es lo que nos está preguntando el problema
- Asignar una literal que represente la incógnita del problema.
- Plantear la ecuación de primer grado traduciendo el enunciado a lenguaje algebraico
- Resolver la ecuación de primer grado. Consiste en encontrar el valor que debe tomar la incógnita para que se cumpla la igualdad.
- Interpretar la solución: Una vez que tenemos la solución de la ecuación (que no es la solución del problema), debemos interpretarla para darle un sentido, obteniendo así la solución del problema.
¡Buen
trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion