En busca del enésimo término
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42
En busca del enésimo término
Aprendizaje esperado: formula expresiones algebraicas de primer grado a partir de sucesiones y las utiliza para analizar propiedades de la sucesión que representan.
Énfasis: determinar la regla general de sucesiones e identificar expresiones equivalentes.
¿Qué vamos a aprender?
Esta sesión te llevará a descubrir nuevos aprendizajes y otras formas de ver a las Matemáticas, ya que en el proceso de formación en el que te encuentras, requiere cada vez mayor dominio de esta materia, para afrontar los distintos retos que conlleva esta etapa de formación como estudiantes, junto con tu desempeño académico.
En esta lección estudiarás el aprendizaje esperado: “Formula expresiones algebraicas de primer grado a partir de sucesiones y las utiliza para analizar propiedades de la sucesión que representan”.
Para ello, resolverás algunos ejercicios y problemas en donde determinarás la regla general de sucesiones aritméticas, figurativas y numéricas e identificando los valores que corresponden a ciertos términos.
Antes de comenzar, no debes olvidar los materiales que vas a utilizar:
- Cuaderno de matemáticas u hojas de rehúso
- Lápiz
- Colores, los cuales puedes utilizar para señalar o identificar lo que consideres más importante durante el desarrollo de la lección
- Tu libro de texto de Matemáticas
Durante el desarrollo de la lección, anota tus dudas, inquietudes o dificultades que surjan al resolver los planteamientos dados; también, te aconsejo que escribas los datos o definiciones que consideres importantes.
¿Qué hacemos?
Como se comentó antes, estudiarás sucesiones aritméticas y te preguntarás. ¿Cuál es la importancia de este tema en las Matemáticas?
Aunque se piensa que las sucesiones solo consisten en una serie de números ordenados, lo cierto es que puedes encontrar aplicaciones de ellas en muchas situaciones; por ejemplo, las sucesiones tienen numerosas aplicaciones en las ciencias de la computación y teoría de juegos.
En la vida cotidiana también puedes aplicarlas. Por ejemplo, al ahorrar cierta cantidad de dinero en algún periodo de tiempo de manera constante, y hacer un cálculo del total ahorrado, considerando determinado número de días. También puedes utilizar una sucesión al momento de dedicar un tiempo específico para ejercitarte e ir aumentando dicho tiempo día con día hasta llegar a cubrir una meta específica.
Incluso en la naturaleza, puedes encontrar con sucesiones, en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo y en la flor de la alcachofa.
A propósito del tema de sucesiones, es importante comentar sobre un valioso aportador a este tema. Se refiere al matemático italiano Leonardo de Pisa, mejor conocido por su sobrenombre, Fibonacci. Una de sus tantas aportaciones a las matemáticas fue la famosa sucesión llamada, la sucesión de Fibonacci. Ésta ha resultado muy fructífera a lo largo de los años y aparece en muy distintas áreas de las matemáticas y la ciencia.
A continuación, te invito a observar un audiovisual para conocer un poco más sobre las sucesiones y sobre Fibonacci, observa del minuto 03:04 a 04:27.
- ¿Qué es una sucesión?
Como pudiste verificar en el audiovisual, las sucesiones se presentan en muchos contextos de la vida.
Analiza la siguiente sucesión de figuras.

La imagen presenta una sucesión compuesta por cuadrados. En esta situación, cabe hacernos una pregunta: ¿Cuántos cuadrados hay en cada figura o término de la sucesión? ¿Cuántos cuadrados formarán la siguiente figura de la sucesión?
El primer término tiene dos cuadrados, el segundo término está formado por cuatro cuadrados, el tercer término, por seis cuadrados, mientras que el cuarto término por ocho cuadrados y el quinto término se conforma por diez cuadrados.
Al escribir el número de cuadrados de cada término o figura, se obtiene la sucesión numérica: 2, 4, 6, 8, 10. Como puedes ver, la sucesión empieza con 2 cuadrados y cada término se obtiene sumando dos más al término anterior; es decir, para obtener cualquier término de la sucesión, debes multiplicar por dos el número del término correspondiente.
Pon a prueba la afirmación anterior:
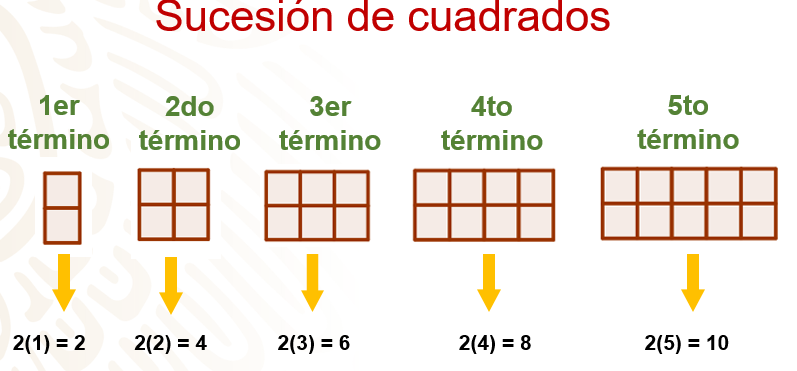
Dos por el primer término de la sucesión; es decir, 2 por 1 es igual a 2.
Dos por el segundo término de la sucesión, 2 por 2 es igual a 4.
Para el tercer término de la sucesión tenemos 2 por 3 es igual a 6 cuadrados.
Par el término 4, 1 por 4 es igual a 8.
Y finalmente se tiene que para el término 5, 2 por 5 es igual a 10 cuadrados.
Este comportamiento, lo puedes establecer por medio de una fórmula, la cual, de ahora en adelante, denominarás regla general de la sucesión.
Como se vio, cada término se obtiene al multiplicar el número del término por 2. En este caso, para obtener el valor del sexto término, basta con multiplicar 6 por 2 que es igual a 12 cuadrados.
Pero ¿habrá una manera de expresar de manera algebraica la regla de la sucesión?
Antes de responder la pregunta, considera que a este tipo se sucesiones se les llama sucesión aritmética. Observa la siguiente información. No te olvides de tomar nota de lo que consideres más relevante.
Una sucesión es un conjunto ordenado de números o figuras que siguen cierto patrón.
Una sucesión aritmética es aquella en la que la diferencia entre términos consecutivos es constante. La regla general que permite obtener el valor de cualquier término de una sucesión aritmética, el cual denominaremos como enésimo término, es: “a” subíndice n, es igual a “a” subíndice 1 más d por el producto de la “n” menos 1.
Donde “an” representa al enésimo término de la sucesión, “a1” representa al primer término de la sucesión, “d” es la diferencia entre términos consecutivos y “n” el número de término del que se quiere obtener su valor.

Con estos elementos, vas a encontrar algebraicamente, la regla de la sucesión anterior, que es: 2, 4, 6, 8, 10.
Sustituyendo los valores de la sucesión en la fórmula general, se tiene que: el primer término es 2, en este caso a subíndice 1 es igual a 2.
Luego, para calcular “d”, que es la diferencia entre términos consecutivos, sean éstos el segundo y el primer término. La diferencia entre 4 y 2 es 2, porque 4 – 2 = 2. Pero también se pueden ocupar otros dos términos a condición de que sean consecutivos, por ejemplo, la diferencia entre el tercer y el segundo término, 6 y 4 es el mismo valor, 2 y así sucesivamente. Entonces “d” es igual a 2.
Así se obtiene que la regla de la sucesión para “an” que es igual a 2 más 2 por la diferencia de “n” menos 1.
Comprueba que la regla se cumple para los tres primeros términos. Sustituye “n” por el número de término 1, 2 y 3, respectivamente y obtienes: a1 = 2 + 2(2 –1), aplicando la jerarquía de operaciones, obtienes que a1 es igual a 2 + 2 por cero, a1 es igual a 2 más cero igual a
Para a2, 2 más 2 por la diferencia de 2 y 1 es igual a 2 más 2 por 1 igual a 2 más 2 igual a 4
Y finalmente resolviendo las operaciones observa que a3 es igual a 6; así compruebas que la regla se cumple.
Verifica, a continuación, otra sucesión de figuras para determinar su regla.
Analiza cada término, identifica al primer término, la diferencia entre términos consecutivos e intenta encontrar la regla de la sucesión.

Analiza la sucesión de figuras que, en este caso, son estrellas. El primer término está formado por 4 estrellas; el segundo término tiene 7 estrellas, en el tercer término hay 10 estrellas y en el cuarto término contamos con trece estrellas.
Al escribir números al término de cada figura tenemos la sucesión: 4, 7, 10, 13.
¿Cuántas estrellas tendrá el quinto y sexto término de la sucesión?
¿Cuál es el primer término?
¿Cuál es la diferencia entre términos consecutivos?
¿Cuál es la regla de la sucesión?
Para determinar la regla de la sucesión, primero identifica que el primer término es el 4 y puedes observar que la diferencia entre términos consecutivos es 3. Con estos datos, ¿ya puedes establecer la regla de la sucesión?
Recuerda que la regla general de las sucesiones aritméticas es an = a1 + d por la diferencia n menos 1.

Entonces, procede a sustituir en la regla general los valores que identificaste para obtener la regla de la sucesión. Tienes que el primer término, es decir “a1” es igual a 4 y que la diferencia entre términos consecutivos es 3.
Por lo tanto, la regla de la sucesión es “an = 4 + 3” por la diferencia de “n” y 1.
Para validar que la regla se cumple, calculemos los términos 3, que ya conocemos, el 5 y el 10.
Para “a3” es igual a 4 más 3 por la diferencia entre 3 y 1; resolviendo las operaciones, se llega a 4 + 6 = 10; para el quinto término, sustituye “n” por el 5 y, al resolver las operaciones, obtienes 16. Si sumas al 4to término, que es 13, la diferencia, que es 3, validas que la regla se cumple.
Ahora calcula el término 10
Sustituye “n” por el 10 y, al resolver las operaciones, obtienes que es igual a 31
Te invito a completar la sucesión numérica que se genera con la sucesión de estrellas, hasta el término 10. Después, utiliza la regla encontrada para validar que se cumple para cada término. ¿Cuántas estrellas tiene el término 20 en la sucesión?
Hasta ahora, has trabajado sucesiones figurativas, que representan sucesiones aritméticas y has establecido su regla o expresión algebraica, la cual has comprobado al calcular diferentes términos de la misma.
Pero, también existen otras formas de obtener la regla de una sucesión aritmética, haciendo un análisis del comportamiento de la sucesión figurativa y puedes encontrar una expresión que resultaría equivalente a una de la forma an = a1 + d (n – 1), que viste en las sucesiones previas.
Analiza el siguiente caso.
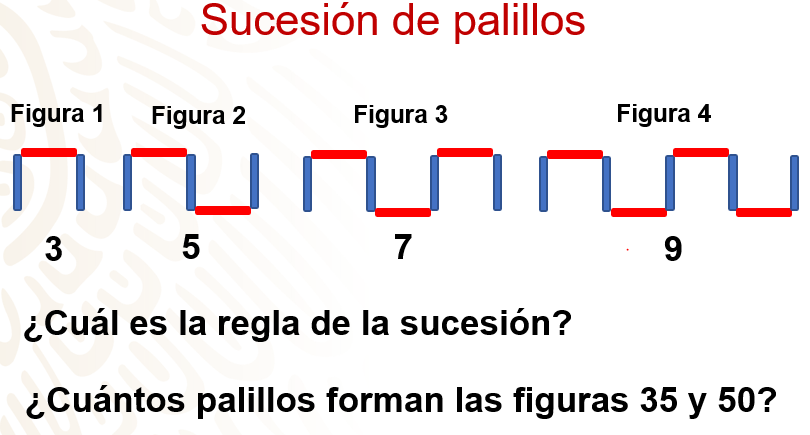
Considera la siguiente sucesión, formada por palillos azules y rojos, ordenados en forma de herradura. La figura 1 está formada por 3 palillos; la figura 2, por 5 palillos; la figura 3, por 7 y la figura 4, por 9; es decir, la sucesión numérica que se genera es 3, 5, 7, 9, …
¿Cuántos palillos forman las figuras 5 y 6? ¿Cuál es la regla de la sucesión? ¿Cuántos palillos forman las figuras 35 y 50?

Para establecer la regla de la sucesión, ¿cuál es la diferencia entre términos consecutivos? La diferencia es 2
Ahora, si multiplicas el primer término o figura por la diferencia, es decir, 1 por 2, ¿qué tienes que hacer con el resultado para obtener el número de palillos de la figura 1?
En este caso, al resultado de la multiplicación que es 2, hay que sumarle uno, ya que 1 por 2 más 1 es igual a 3
Ahora ve el caso de la figura 2, si multiplicas el número de término o figura por la diferencia, es decir, 2 por 2 que es igual a 4, al resultado tienes que sumarle 1 para obtener el número de palillos: 2 por 2 + 1 = 5
Si repites la misma secuencia de operaciones para las figuras 3 y 4, puedes ver que se cumple el mismo patrón: 3 por 2 más 1 es igual a 7 y 4 por 2 más 1 es igual a 9
Ahora, si llamas “an” a cualquier figura de la sucesión, ¿cómo puedes determinar la expresión que permite saber los palillos que la forman a la figura ene?
La expresión es an = n por 2 más 1 que es igual a 2n más 1.
Cómo pudiste ver, se encontró otra manera de obtener y representar la regla de una sucesión aritmética, en este caso es de la forma an = dn + b, donde d es igual a la diferencia entre términos consecutivos y b es una constante.
Esta expresión es equivalente a la expresión general vista antes.
Para validar lo anterior, calcula las primeras 4 figuras de la sucesión, utilizando las dos reglas generales vistas y para responder la pregunta: ¿Cuántos palillos forman las figuras 35 y 50?
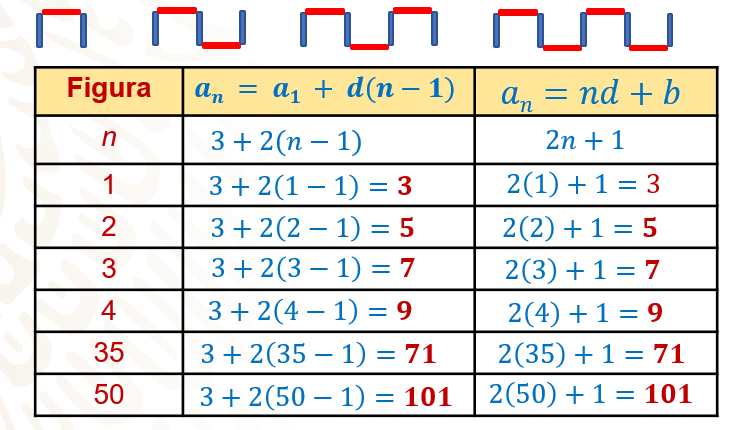
Coloca en una tabla la información de la sucesión, en la primera columna el número de figura o término de la sucesión y colocas en las siguientes columnas las dos expresiones generales de una sucesión aritmética: primero “an = a1 más d(n –1)” y después, “an = nd + b”.
En el caso de la sucesión de palillos, la expresión dada en la primera forma para determinar ene es: primer término 3, diferencia 2, por lo tanto, la regla queda como: 3 + 2 por la diferencia n menos 1; la segunda forma la expresión de la regla es 2n + 1, como viste antes.
Ya con las reglas definidas para ene, calcula el número de palillos de la primera figura, utilizando ambas reglas, con la primera regla; 3 por 2 por la diferencia 1-1 es igual a 2 + 2 por 0 igual a 3; con la segunda regla: 2 por 1 más 1 es igual a 3. Como viste en la tabla, al resolver las operaciones, para la figura 2 obtienes 5 en ambos casos: para la 3, 7 y para la 4, 9 palillos.
Ahora, calcula el número de palillos en la figura 35: 3 más 2 por la diferencia 35 menos 1, es igual a 3 más 2 por 34, igual a 3 más 68 igual a 71 palillos, para la segunda regla, se tiene 2 por 35 más 1 que es igual a 71 y la figura 50, como puedes ver, está formada por 101 palillos.
Así, compruebas que ambas expresiones son equivalentes y que cualquiera de ellas te permite obtener cualquier término de la sucesión.
Como reto, utiliza las reglas vistas y determina cuántos palillos forman las figuras 20, 85 y 110 de la sucesión
Las reglas son:
“3 + 2(n – 1)” y “2n + 1”.
Te invito a retomar las sucesiones de cuadrados y de estrellas que viste al inicio de la sesión para expresar su regla de la forma “ad + b”.
Toma nota de la información para que puedas resolver el siguiente problema.
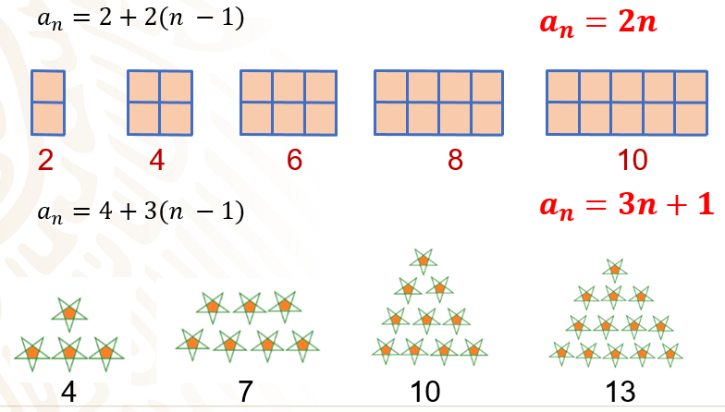
Analiza nuevamente las sucesiones, ¿ya pudiste identificar la regla en cada caso?
En el caso de la sucesión de cuadrados, la diferencia es 2, al multiplicar 2 por el número de cuadrados del primer término; es decir, 2 por 1 igual a 2, por lo que ya no hay que sumar o restar una cantidad. Entonces, en este caso “b” es igual a cero. Si realizas el mismo procedimiento con las otras figuras, se repite el mismo patrón, por lo que la regla queda como an = 2n.
Para la sucesión de estrellas, se sabe que la diferencia es 3, al multiplicar el tercer término por la diferencia, es decir, 3 por 3 el resultado es 9, al cual se tiene que sumarle 1 para obtener el número de estrellas correspondientes a este término. Si realizas lo mismo para el término 2, vemos que 3 por 1 más 1 es igual a 7. Por lo tanto, la regla de la sucesión de estrellas queda como: “an = 3n +1”.
Te invito a utilizar las reglas encontradas para determinar el número de figuras de los términos 30, 65 y 78 de ambas sucesiones.
Si tienes oportunidad, comparte tus respuestas con tu maestra o maestro para recibir retroalimentación.
El reto de hoy:
Para finalizar, te propongo un reto, establecer la regla o expresión algebraica de las sucesiones que se mostrarán enseguida, de dos maneras diferentes.

Observa las sucesiones, identifica el primer término y la diferencia en cada caso.
Las sucesiones numéricas son: 5, 9, 13, 17.
La segunda es: 1, 6, 11, 16, … y la tercera: 6, 10, 14, 18.
¿Pudiste identificar los valores necesarios para establecer las reglas?

Para la sucesión “5, 9, 13, 17, …” las reglas son: “an = 5 + 4(n – 1)” y “an = 4n + 1”.
Para la sucesión “1, 6, 11, 16, …” las reglas son: “an = 1 + 5(n – 1)” y “an = 5n – 4”.
Y para “6, 10, 14, 18, …” las reglas son: “an = 6 + 4(n – 1)” y “4n + 2”.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion