El volumen

El volumen

Aprendizaje esperado: calcula el volumen de prismas y cilindros.

Énfasis: resolver problemas que impliquen el cálculo del volumen de prismas rectos.

¿Qué vamos a aprender?

Conocerás cómo resolver problemas que impliquen el cálculo del volumen de cuerpos geométricos, específicamente el volumen de prismas rectos, cuya base sea un polígono regular. Además, identificarás qué sucede cuando se desconoce alguna de las dimensiones del prisma, es decir, cuando uno de los datos es desconocido.

¿Qué hacemos?

Analiza la siguiente situación-problema. Considera que el volumen en Matemáticas se refiere al espacio tridimensional que ocupa un cuerpo geométrico.

Situación-problema. Caja rectangular

Gerardo es carpintero y armó una caja rectangular de madera que mide 90 centímetros de largo, 40 cm de ancho y 60 centímetros de altura.

¿Cuál es el volumen de la caja de madera?

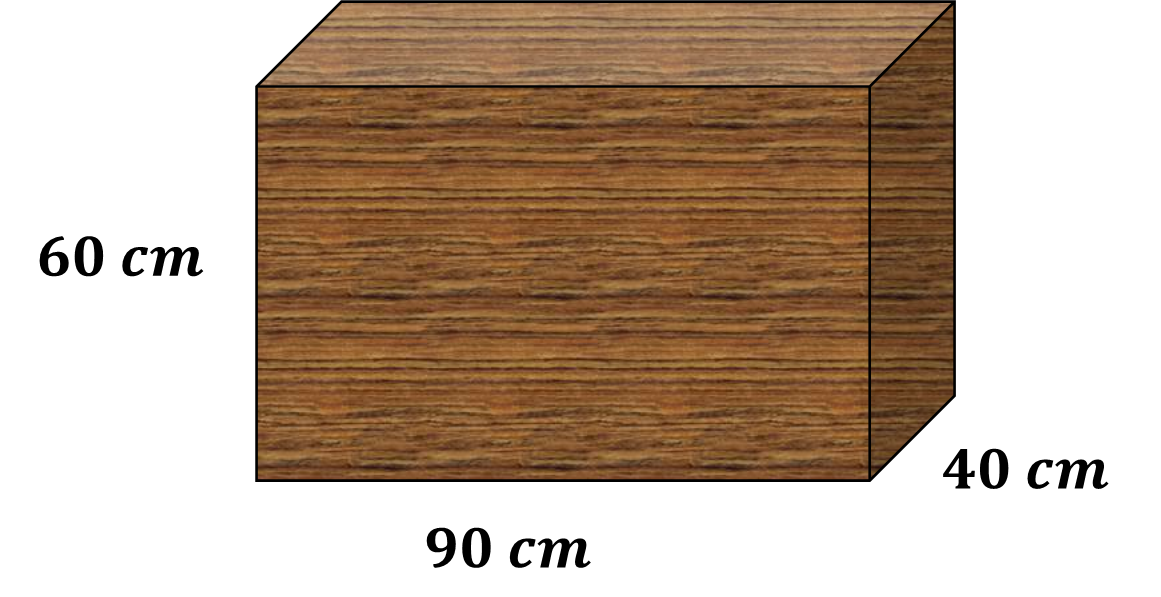
Para dar respuesta a la pregunta del problema, primero analiza la forma que tiene el cuerpo geométrico de la caja; es decir se trata de un prisma recto.

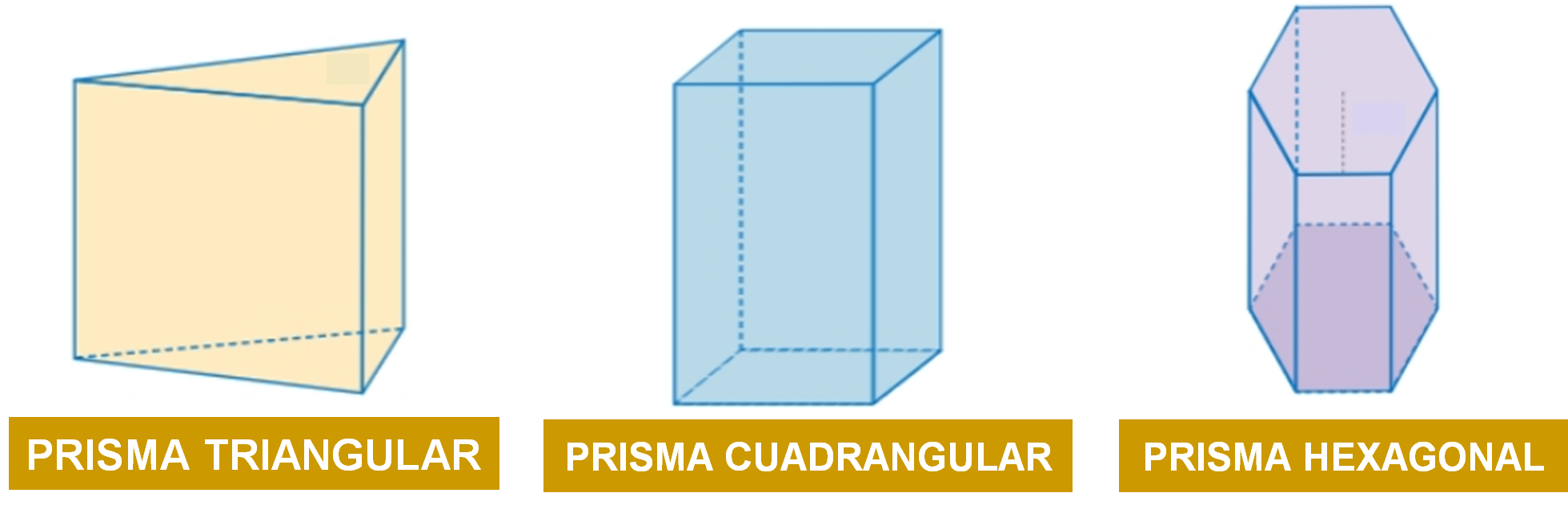
Un prisma es un cuerpo geométrico que está limitado por dos polígonos planos, paralelos e iguales, que se llaman bases; y por otros tantos paralelogramos, como número de lados tengan dichas bases. Según la forma de sus bases, pueden ser triangulares, rectangulares, cuadrangulares, pentagonales, poligonales, entre otros. Un prisma recto es aquel cuyas caras laterales son rectangulares.

Con base en la información anterior, de esta manera se nombra a los prismas, considerando la forma de la base; por ejemplo, si la base es un triángulo, se trata de un prisma triangular recto; si la base es un rectángulo, se trata de un prisma rectangular recto; si la base es un hexágono, se trata de un prisma hexagonal recto; y así se nombran de acuerdo con la forma de los polígonos que forman las bases.

¿Qué nombre recibe el cuerpo geométrico que tiene la forma de la caja? Y, ¿por qué recibe dicho nombre?

Como la base es un rectángulo y sus caras laterales son rectangulares, entonces es un prisma rectangular recto.

Si observas el prisma, se identifica que tiene dos bases rectangulares iguales, por lo que se trata de un prisma rectangular recto. En este prisma, el rectángulo de la base mide 40 centímetros de ancho por 90 centímetros de largo, mientras que la altura es de 60 centímetros.

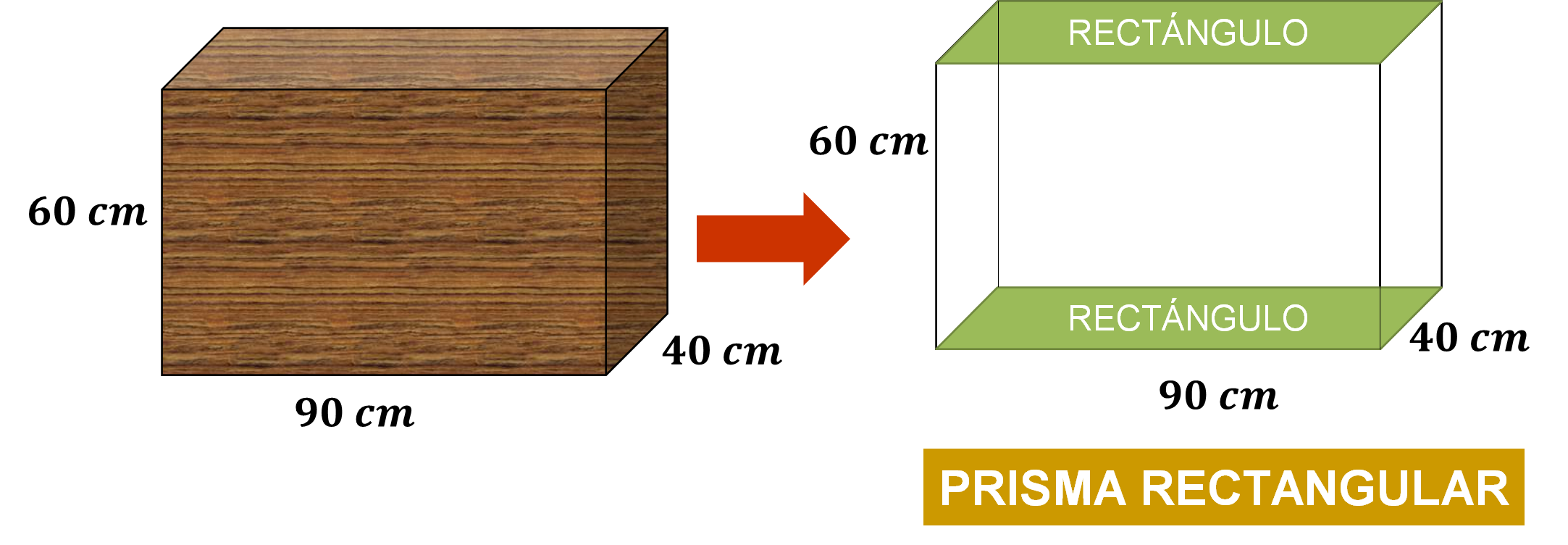
Ahora que ya tienes claro que la caja tiene forma de un prisma rectangular, ¿cómo se determina su volumen?

Para expresar la medida del volumen de un cuerpo geométrico, se utilizan unidades cúbicas: metros cúbicos, centímetros cúbicos, decímetros cúbicos y otras unidades conocidas.

En este sentido, el volumen de un cuerpo es equivalente al número de veces que cabe una unidad cúbica en él.

De manera que, para medir el espacio o volumen que ocupa un prisma rectangular, se pueden contar la cantidad de unidades cúbicas que puede contener, una por una, o bien, calcular el área de la base y multiplicar el resultado por la medida de la altura.

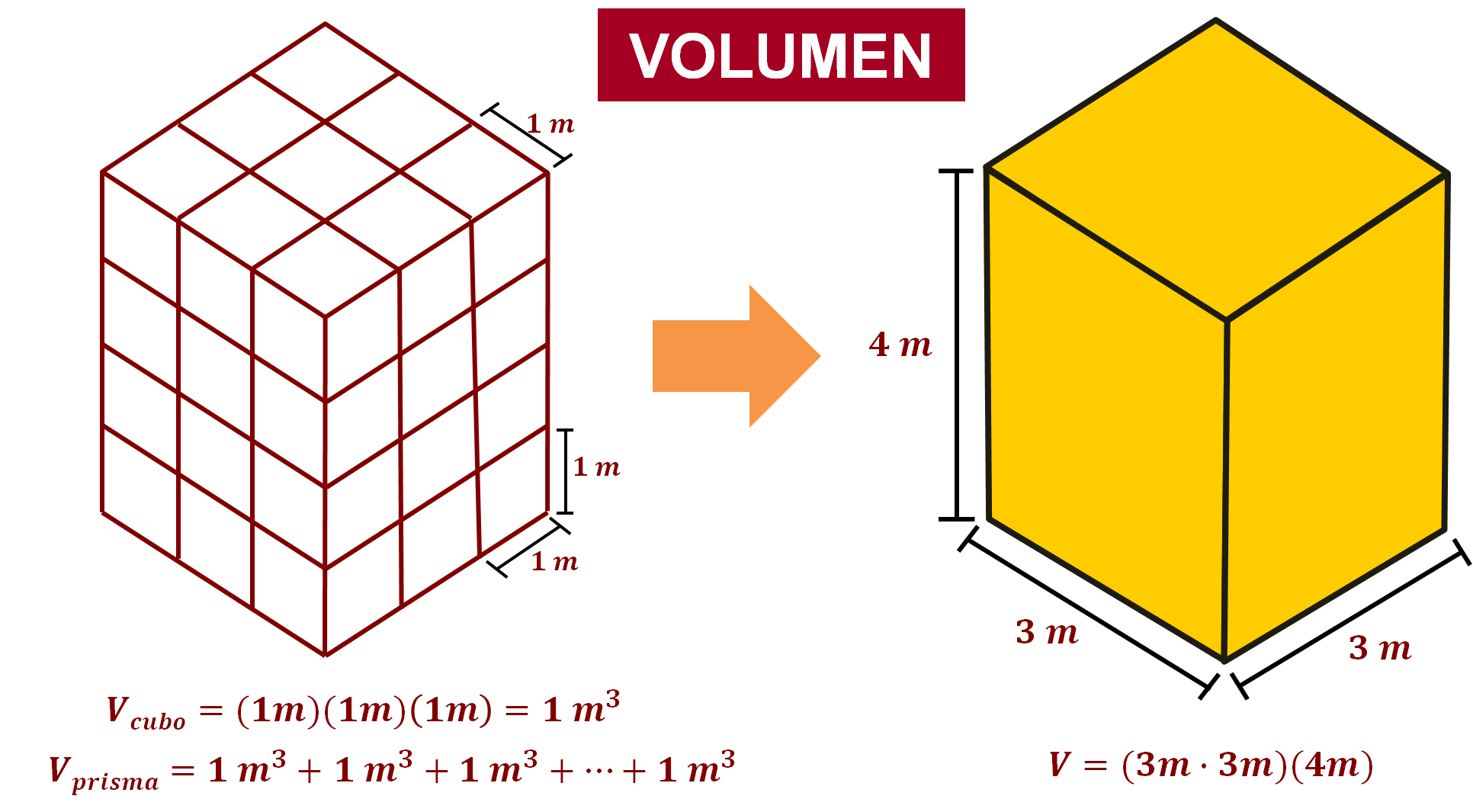
Este proceso se generaliza en la expresión:

Volumen es igual al producto del área de la base por la altura del prisma

En donde V representa al volumen del prisma, Ab representa el área de la base, que puede tener la forma de cualquier polígono regular o irregular; y h, que representa la altura del prisma. Observa la siguiente imagen:

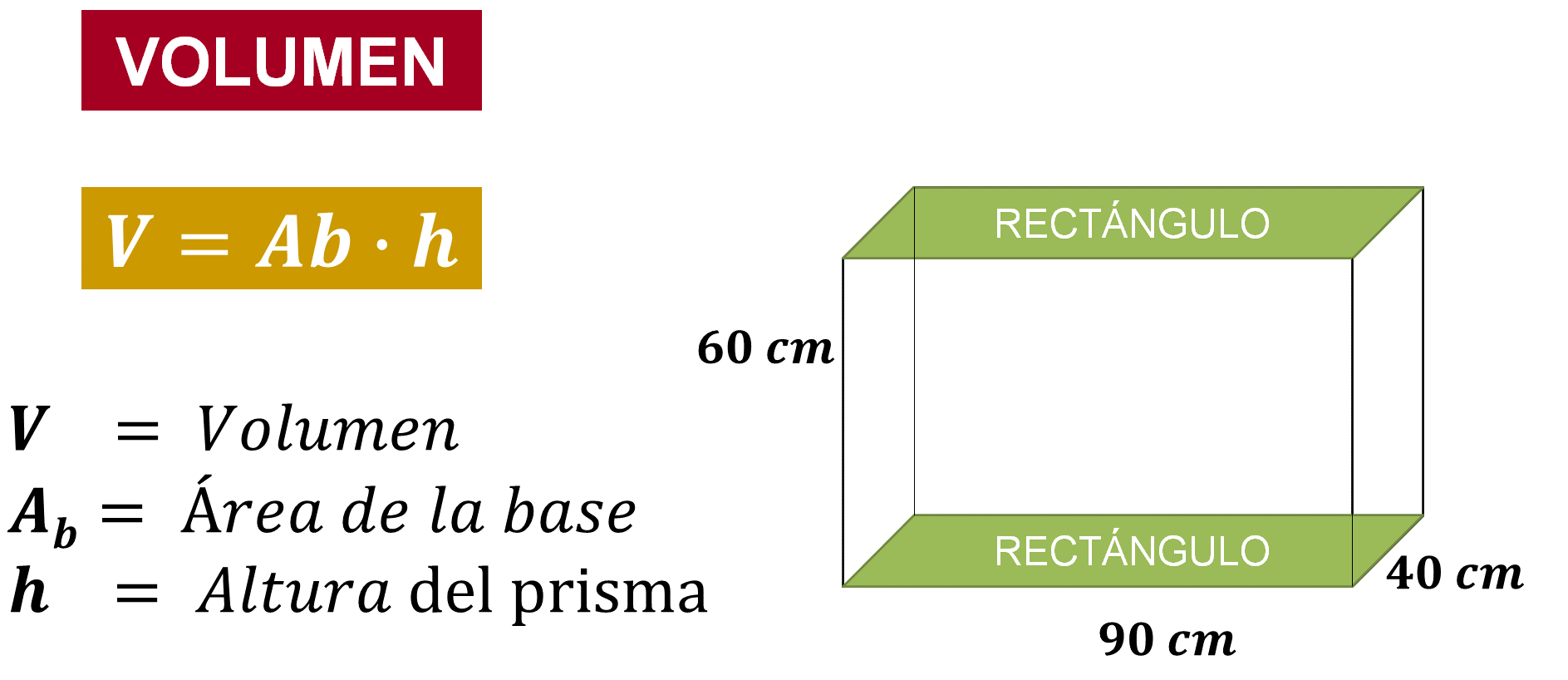
Con esta información, ya puedes resolver el problema.

Para calcular el volumen del prisma de base rectangular, utiliza la fórmula antes mencionada, y para ello es necesario calcular, en primer lugar, el área de la base.

Como la base es un rectángulo que mide 90 centímetros por 40 centímetros, utilizarás la fórmula para calcular el área de un rectángulo. Es decir, el producto de la medida de la base por la medida de la altura del rectángulo, en este caso, el largo por el ancho.

Observa la imagen que aparece a continuación:

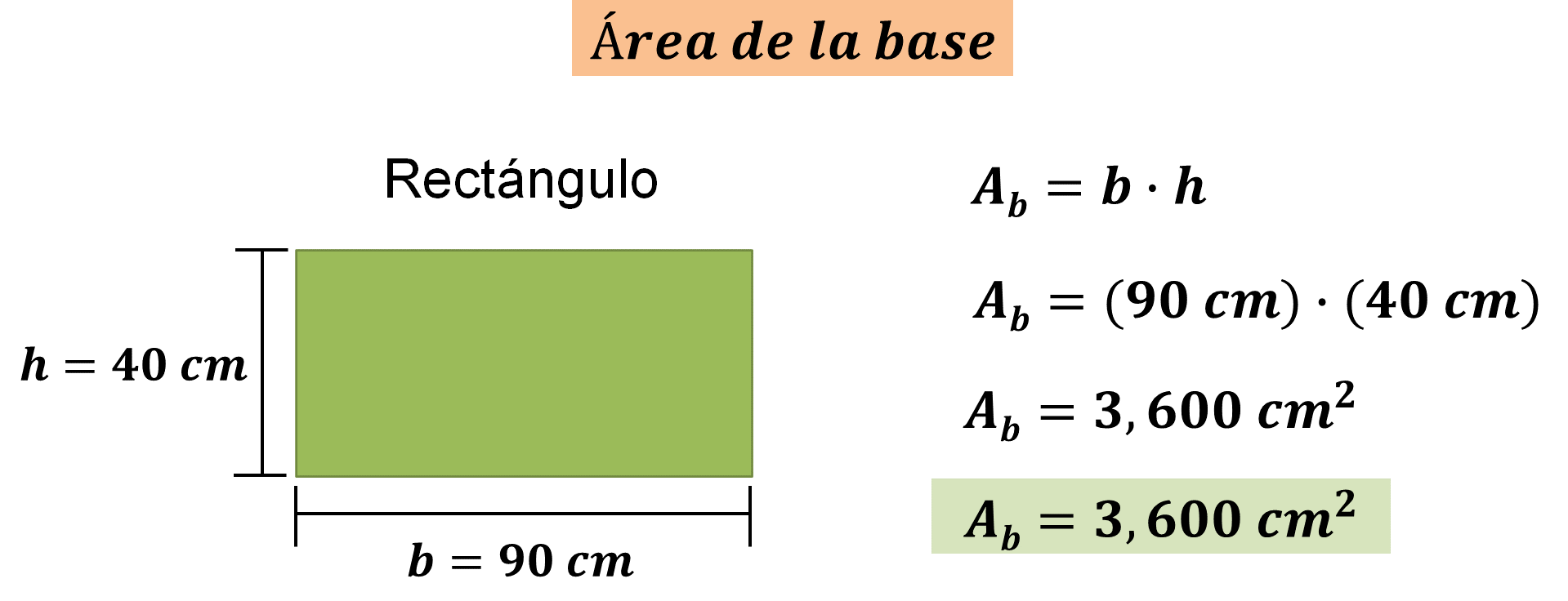
La base del prisma tiene forma rectangular, lo primero es sustituir los datos en la fórmula anterior para calcular el área del rectángulo.

Por lo tanto, se tiene que el área de la base del prisma es de 3600 centímetros cuadrados.

Entonces, este valor de 3600 centímetros cuadrados es el que vas a sustituir en la fórmula para calcular el volumen del prisma. Pero antes es importante que recuerdes que la manera de calcular el área de la base de un prisma dependerá siempre de la forma que tenga la base, que puede ser cualquier polígono, el proceso es diferente en cada caso; por eso es indispensable conocer y analizar las características del cuerpo geométrico antes de calcular el volumen.

Continúa con el volumen del prisma.

Ya que conoces el área de la base, sustitúyela en la fórmula para calcular el volumen, el cual se obtiene a partir del producto de 3600 centímetros cuadrados por los 60 centímetros de altura del prisma:

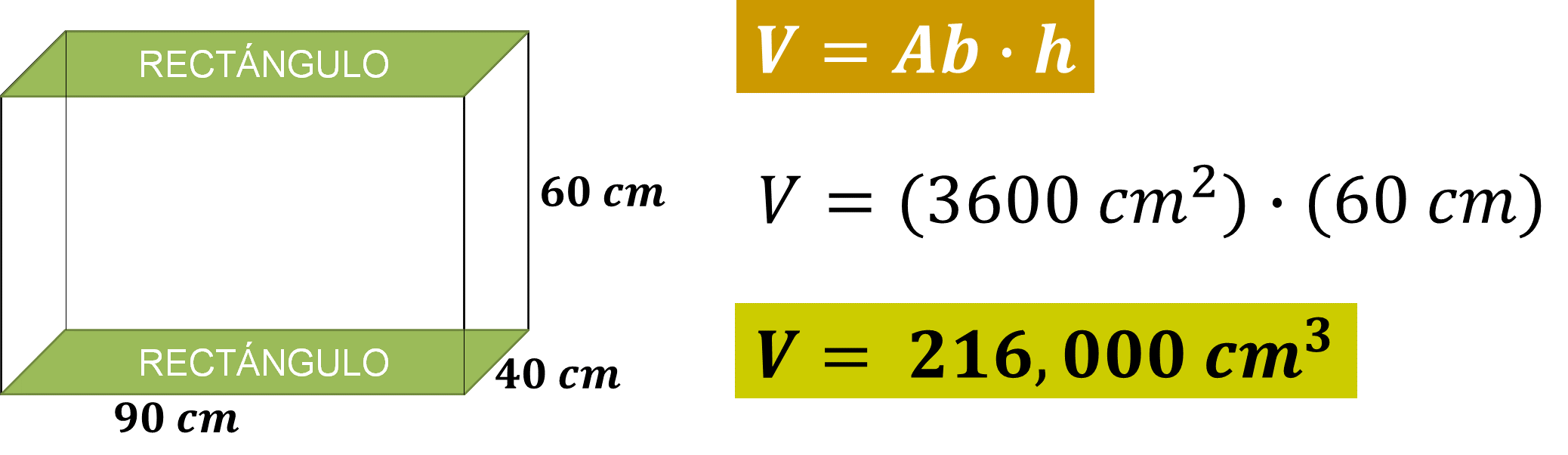
De modo que, el volumen que ocupa la caja es de 216,000 centímetros cúbicos.

El resultado se expresa en unidades cúbicas, las que se han obtenido del producto de los centímetros cuadrados del área de la base, por los centímetros lineales de la altura del prisma rectangular.

A continuación, analiza cómo resolver algunas situaciones-problema en donde la base no es un rectángulo.

Situación-problema. Cubo

Ahora que conoces el volumen de la caja rectangular, Gerardo quiere hacer otra caja de madera que tenga el mismo volumen, pero con forma de cubo.

¿Cuáles son las dimensiones que deberá tener la caja?

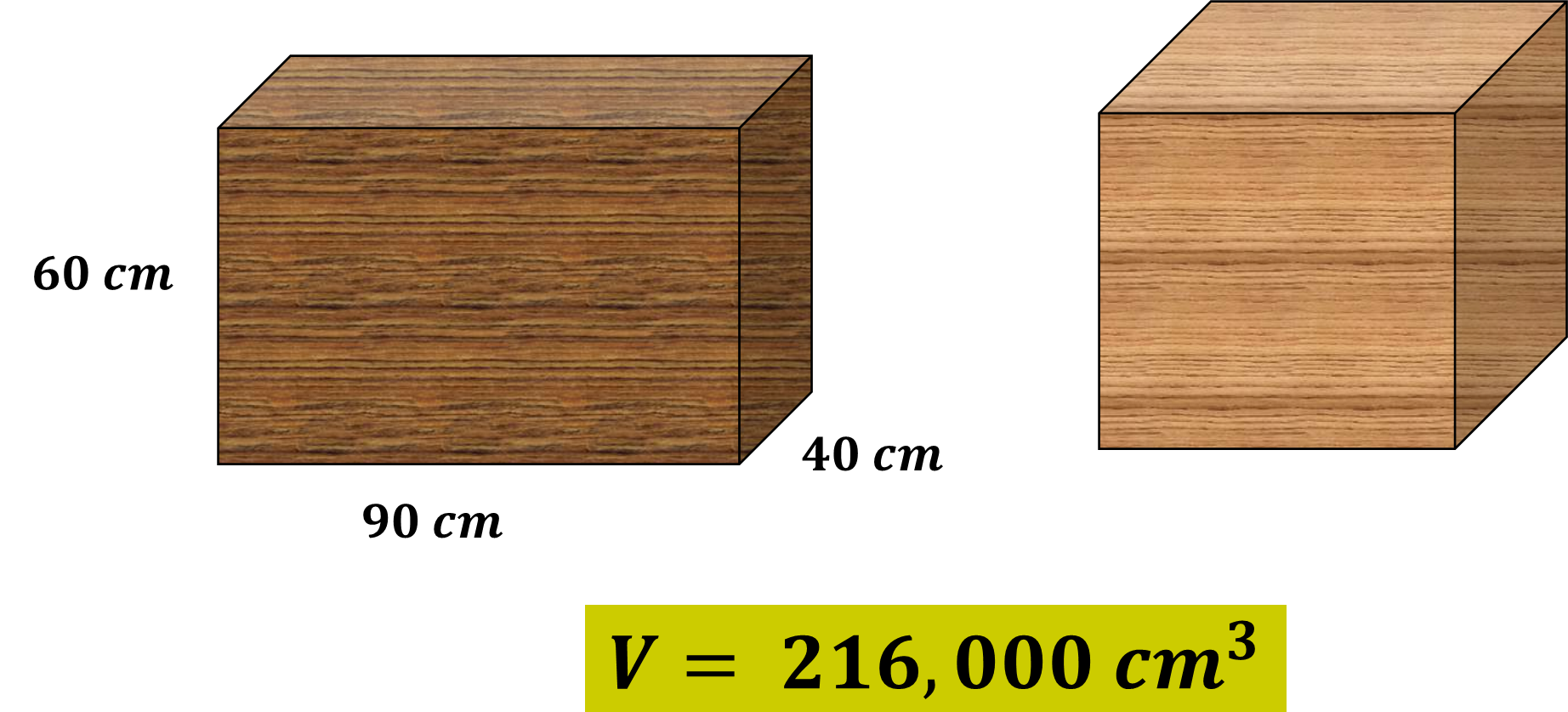
Un cubo es un hexaedro, el cual puede ser clasificado como un paralelepípedo, recto y rectangular, pues sus seis caras tienen forma de cuadrado y son paralelos dos a dos.

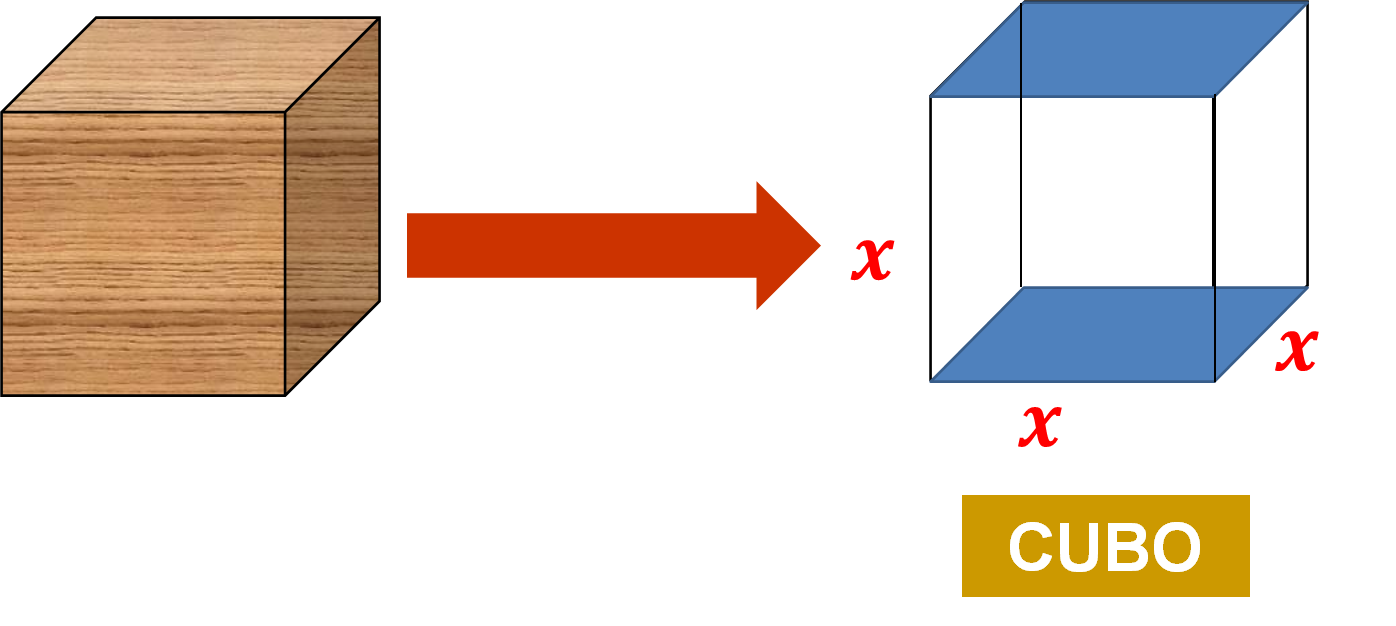
Lo anterior, permite considerar que un cubo se puede clasificar como un prisma recto, cuya base es un cuadrado y su altura es equivalente al lado de la base.

En la imagen anterior, puedes observar que el cubo tiene tres dimensiones, largo, ancho y altura; y todas ellas miden “x”, un valor aún no definido, pero que es el mismo, porque sus caras son cuadradas.

De esta manera, necesitas conocer la medida de las dimensiones de ese cuerpo geométrico, por lo que buscarás un número que elevado al cubo (es decir, un número que multiplicado por sí mismo tres veces) dé como producto 216 000 centímetros cúbicos.

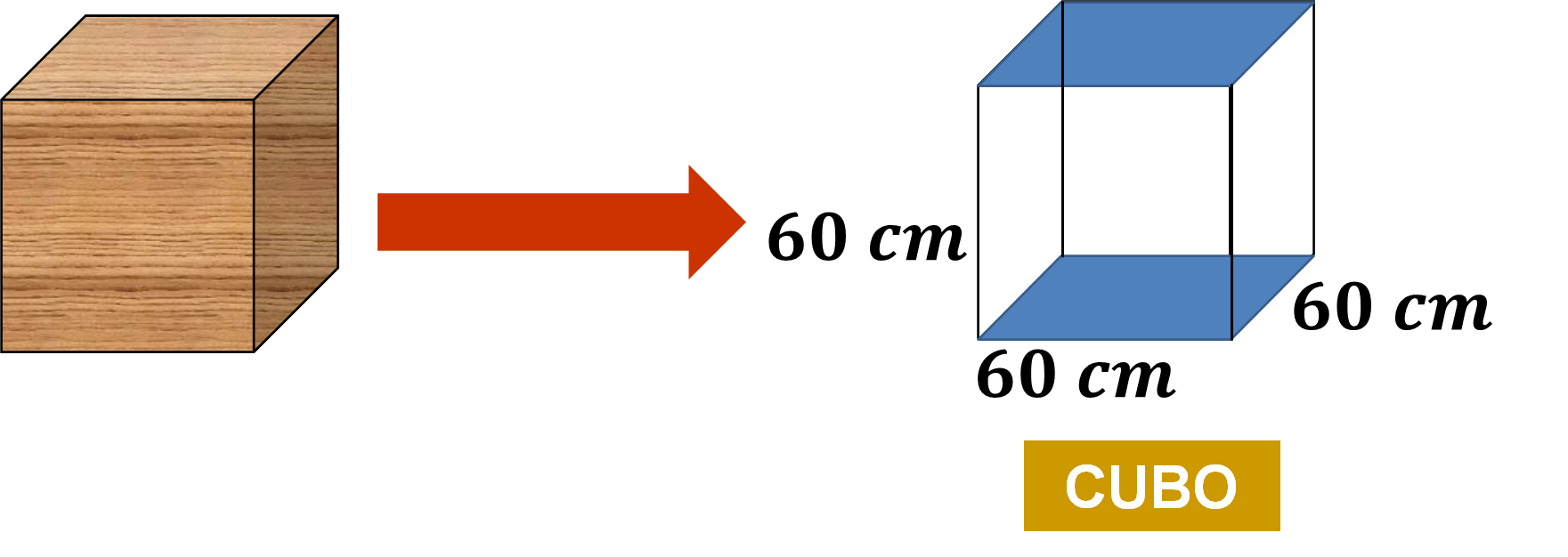
El número que cumple con esta condición es el 60, porque 60 por 60 es igual a 3600, que al multiplicarlo por 60, es igual a 216 000. Comprueba esta información calculando el volumen de la caja cúbica.

Considera que primero debes calcular el área de la base.

Por las características que ya se mencionaron, se sabe que la base del cubo puede ser cualquiera de sus seis caras cuadradas que miden 60 centímetros de lado o de arista.

Siguiendo el procedimiento, para calcular el área de un cuadrado, multiplica lado por lado; es decir, utiliza la fórmula:

Área es igual al producto de la medida de los lados del cuadrado

Y si calculas la medida del área de la base, es decir, el área del cuadrado; debes multiplicar sesenta centímetros por sesenta centímetros:

Y el resultado es, 3600 centímetros cuadrados.

Una vez que determinaste el área de la base, sustituye este valor en la fórmula para calcular el volumen del cubo.

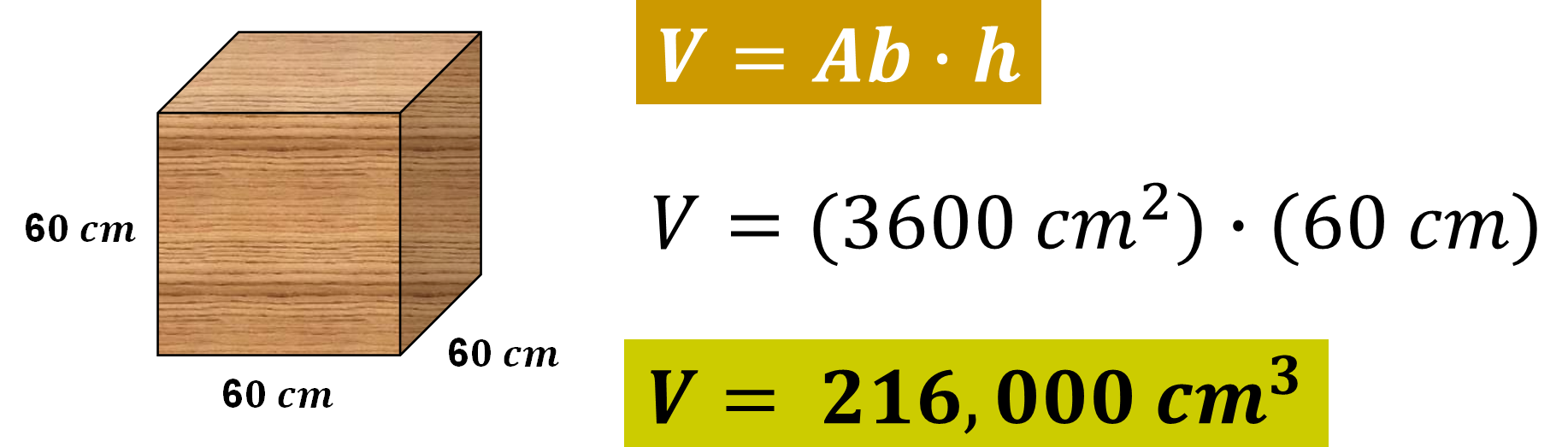
De esta manera, sabes que el volumen es de 216,000 centímetros cúbicos.

Se comprueba que ambas cajas tienen el mismo espacio o volumen, que era lo que buscaba Gerardo.

Ahora, observa qué sucede cuando la figura de la base es un hexágono regular. Resuelve la siguiente situación-problema.

Situación-problema. Hexágono

Fernando tiene una papelería y hace un par de meses comenzó a elaborar manualmente cajas de regalo que luego vende en su negocio. Se ha dado cuenta que es necesario conocer el volumen que tiene cada una de sus cajas, con el fin de brindar un mejor servicio, y de esta manera ofrecer más detalles que ayuden a sus clientes a decidir qué caja les conviene comprar.

Una de las más vendidas es una caja con forma de prisma recto de base hexagonal. Ayuda a Fernando a calcular el volumen de la caja.

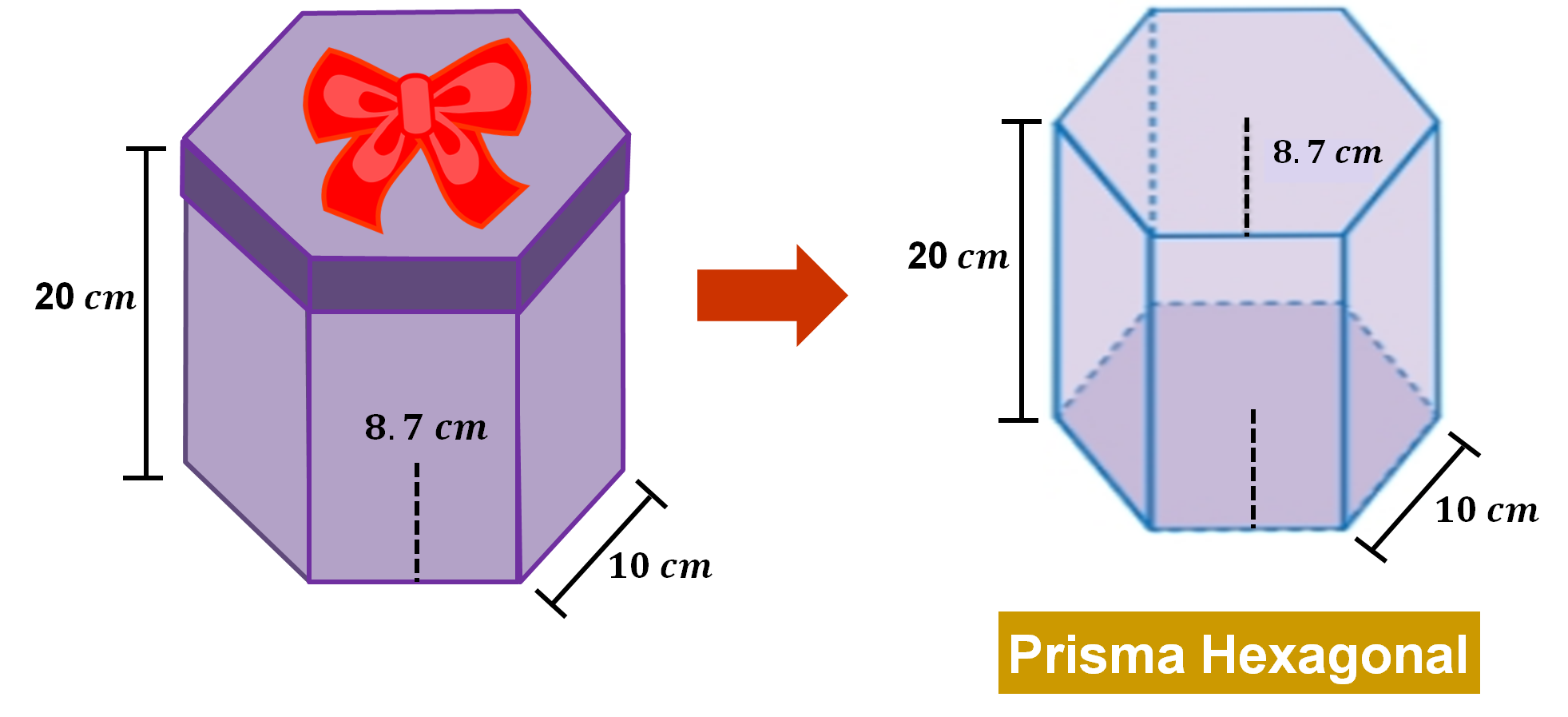
Para que Fernando pueda ayudar a sus clientes a decidir, se tiene que calcular el volumen de la caja.

Para ello, se necesita primero calcular el área de la base, que es un hexágono regular y después obtener el volumen del prisma multiplicando el valor que se encuentre del área de la base por la altura de la caja.

La fórmula para calcular el área de un hexágono regular es:

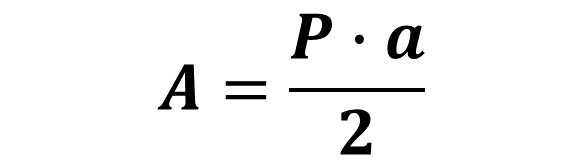
De manera que, para calcular el área de la base con forma de hexágono regular, primero tienes que calcular su perímetro.

Como se trata de un polígono regular, la medida de los 6 lados de la figura es la misma. En este caso, el perímetro se obtiene al sumar la medida de los 6 lados del hexágono que es de 10 centímetros:

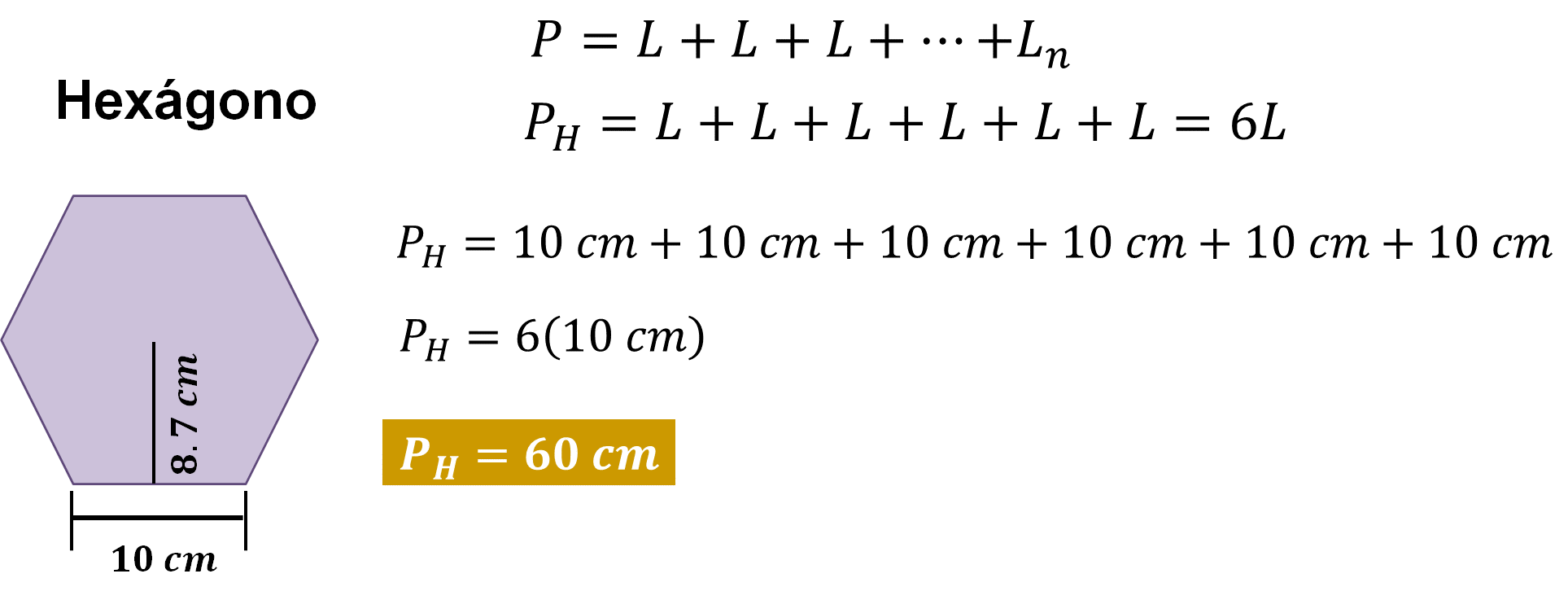
De esta manera el perímetro es de 60 centímetros lineales.

Ahora, el resultado que obtuviste, lo vas a utilizar para calcular el área del hexágono.

Sabiendo que el perímetro es de 60 centímetros y la apotema mide aproximadamente 8.7 centímetros:

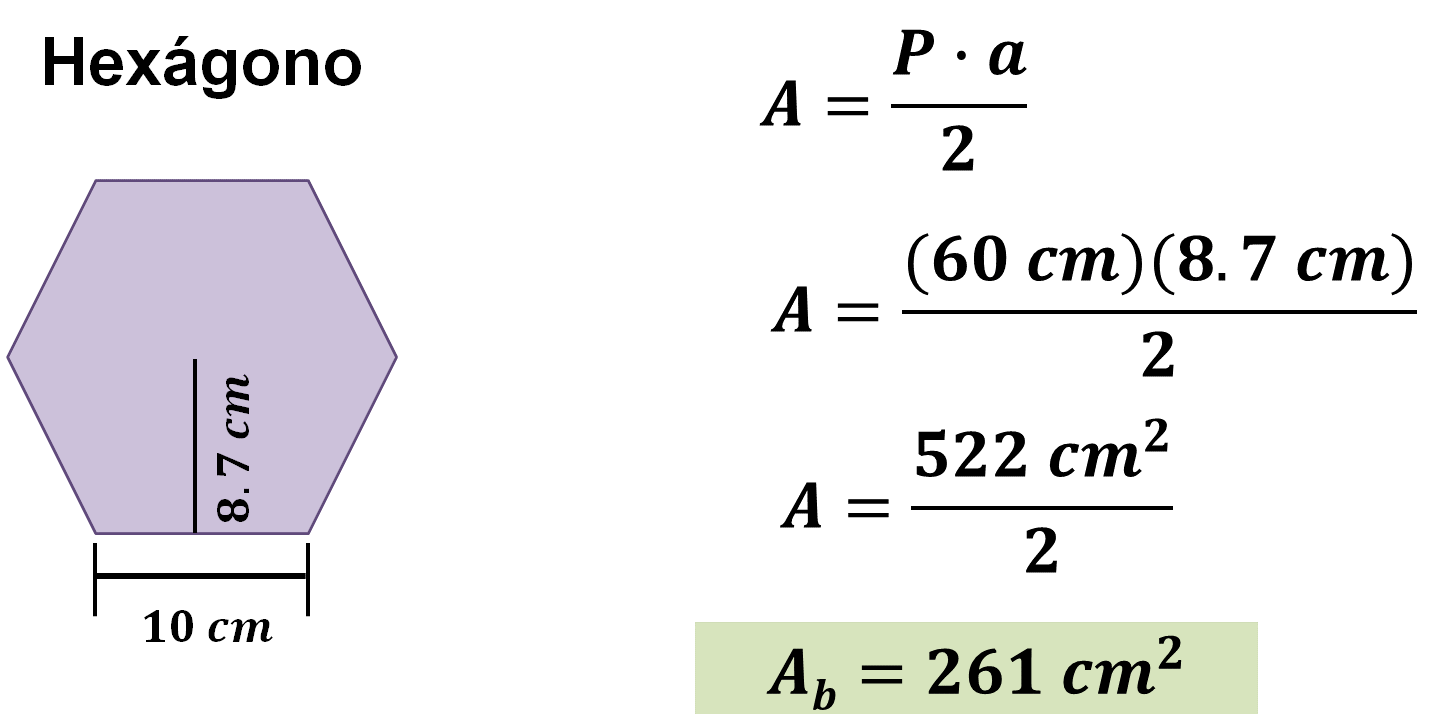
Con lo cual se obtienen 261 centímetros cuadrados, es decir, que el área del hexágono de la base del prisma es de 261 centímetros cuadrados.

Ahora que ya conoces el área de la base, puedes calcular el volumen de la caja de regalo con forma de prisma con base hexagonal.

Para ello, sustituye el área de la base, que es 261 centímetros cuadros en la fórmula, para calcular el volumen del prisma hexagonal, y multiplica por la medida de su altura, la cual es 20 centímetros:

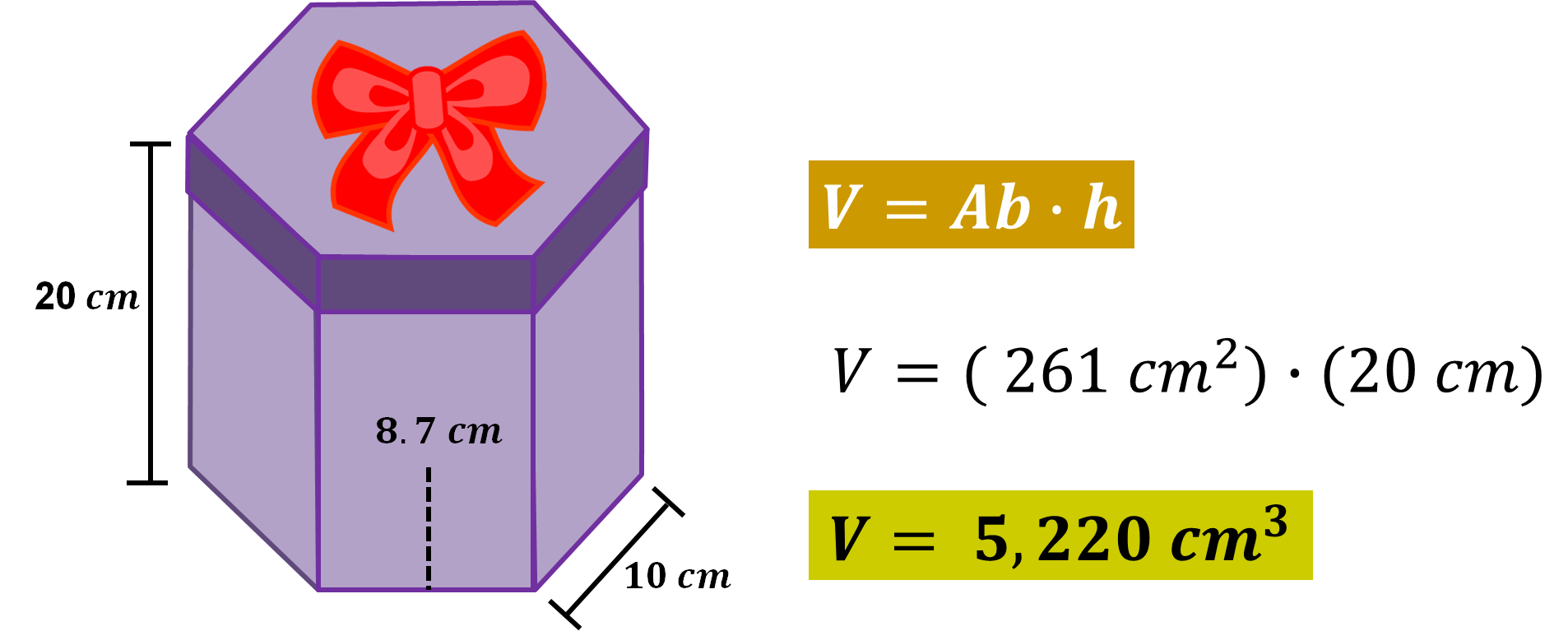
Así obtienes el volumen de la caja que es, 5,220 centímetros cúbicos.

Resuelto lo anterior. Analiza otra situación-problema.

Situación-problema. Prisma pentagonal

Una piscina tiene forma de prisma pentagonal recto. Su volumen es de 125 metros cúbicos y el área de la base es de 50 metros cuadrados.

¿Cuál es la altura de la piscina?

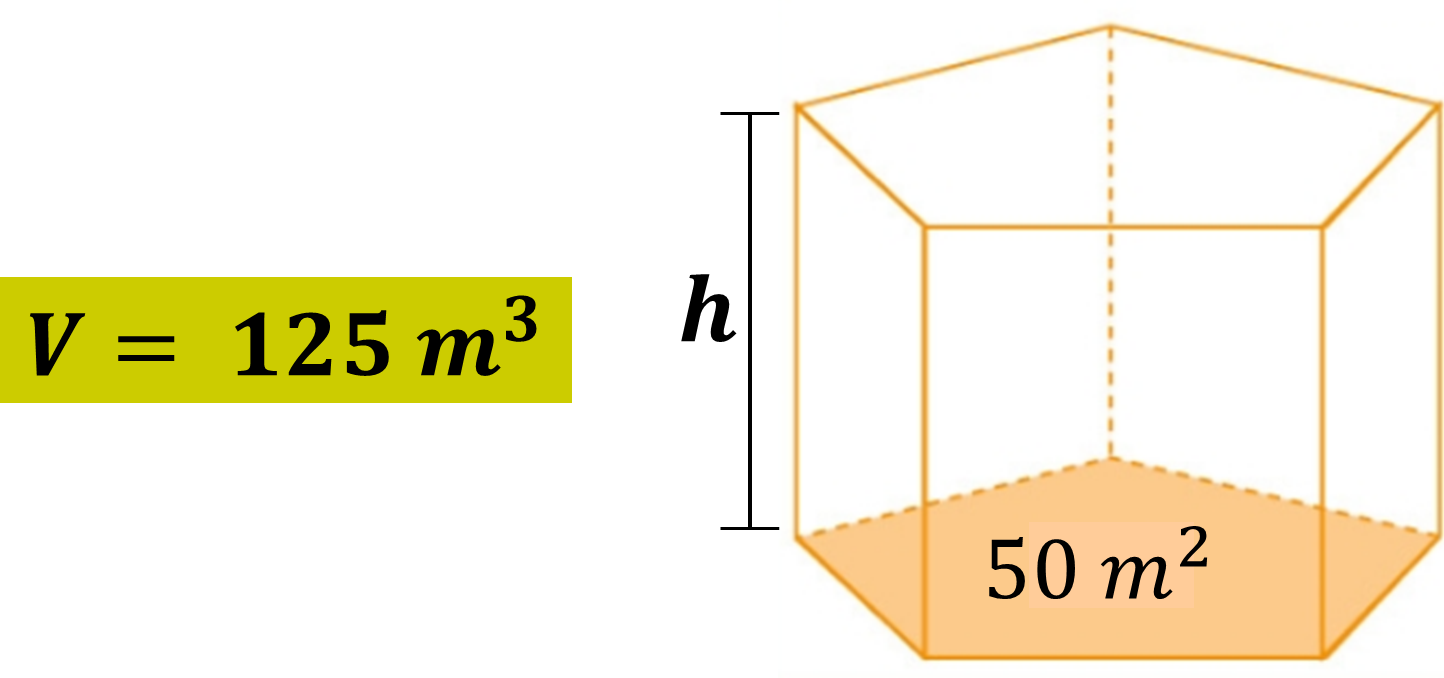
¿Cómo puedes utilizar los conocimientos que has adquirido hasta este momento para calcular su altura?

Observa que la piscina tiene forma de prisma pentagonal, cuyo volumen es de 125 metros cúbicos; y 50 metros cuadrados es el área de la base.

La fórmula para calcular el volumen de un prisma es: Volumen es igual al producto del área de la base por la altura; aunque la fórmula no te llevará directamente al resultado, puedes observar que el dato que se busca forma parte de la fórmula para calcular el volumen del prisma.

Para ello, sustituirás los datos que conoces en la fórmula para calcular el volumen de un prisma.

De esta manera tienes que:

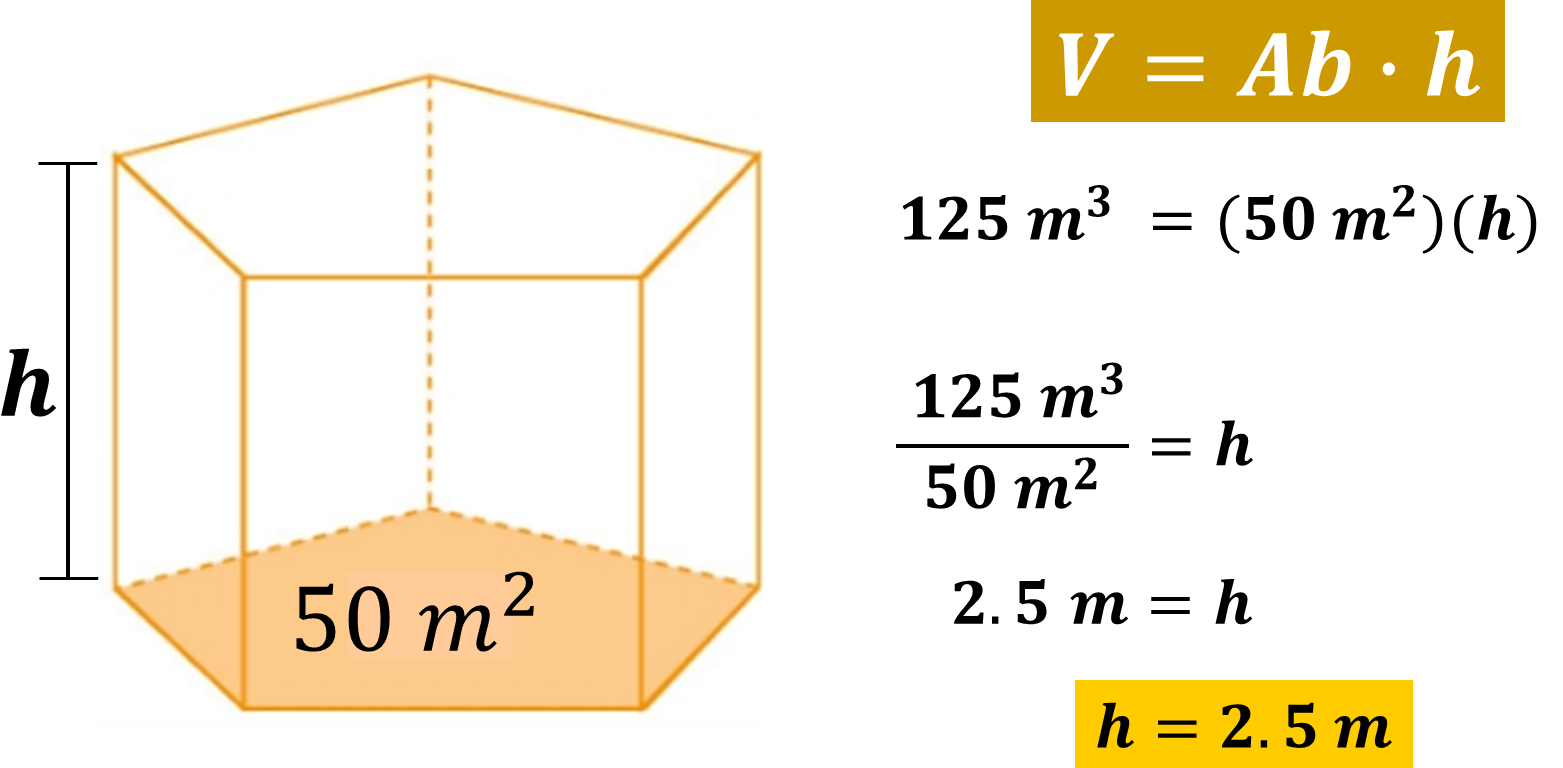
El volumen de la piscina es de ciento veinticinco metros cúbicos, que es igual al producto del área de la base, que mide 50 metros cuadrados por su la altura H, que hasta el momento se desconoce.

Una manera de determinar su altura es buscar un número tal que al multiplicarlo por 50 se obtenga 125.

Otra manera de determinarlo es dividiendo ciento veinticinco metros cúbicos entre cincuenta metros cuadrados, que es igual a 2.5 metros.

Esto quiere decir que la altura o profundidad de la piscina es de 2.5 metros, ya que 2.5m x 50 metros cuadrados = 125 metros cúbicos.

Para calcular la altura de cualquier prisma, necesitas conocer la medida del área de la base y el volumen del prisma dado; puedes utilizar, para calcular la altura de un prisma, la siguiente relación expresada como cociente:

¿Qué sucede si la medida que se desconoce es el área de la base o incluso uno de los lados de la figura? ¿El procedimiento es el mismo?

Para responder la pregunta anterior, analiza otra situación-problema, y observa lo que sucede.

Situación-problema. Piscina rectangular

Una piscina tiene forma de prisma rectangular, se sabe que su volumen es de 300 metros cúbicos, que mide 3 metros de altura o profundidad, y 20 metros de largo.

¿Cuál es la medida del ancho?

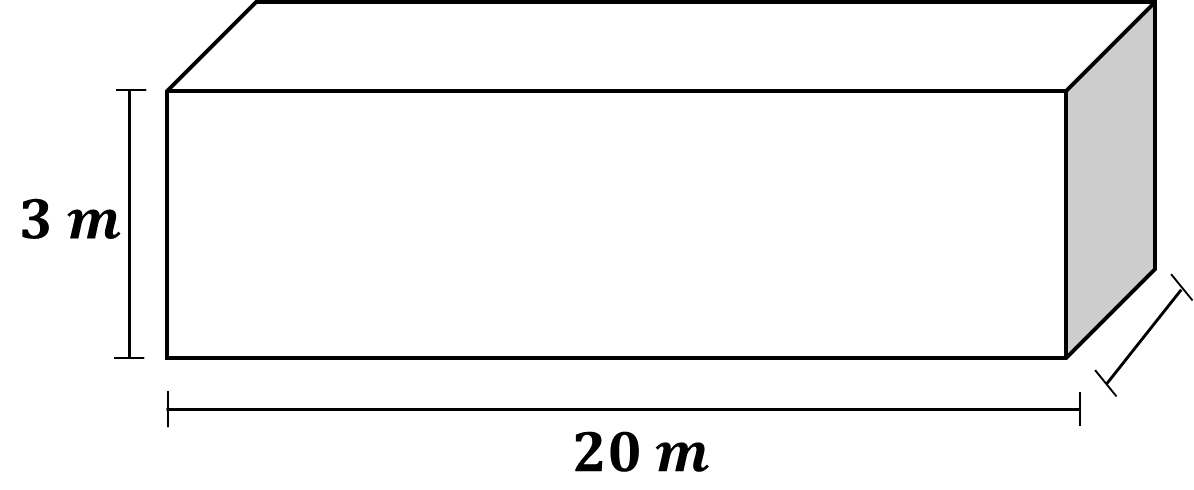
La piscina tiene forma de prisma rectangular, porque la base es un rectángulo de 20 metros de largo. En esta ocasión, buscarás la medida del ancho del rectángulo de la base, sabiendo que el volumen es de 300 metros cúbicos y la medida de la altura es de 3 metros.

Dado que la medida que se busca es el ancho del rectángulo del área de la base del prisma, es necesario conocer el área de la base, de esta manera podrás encontrar la medida del ancho del rectángulo.

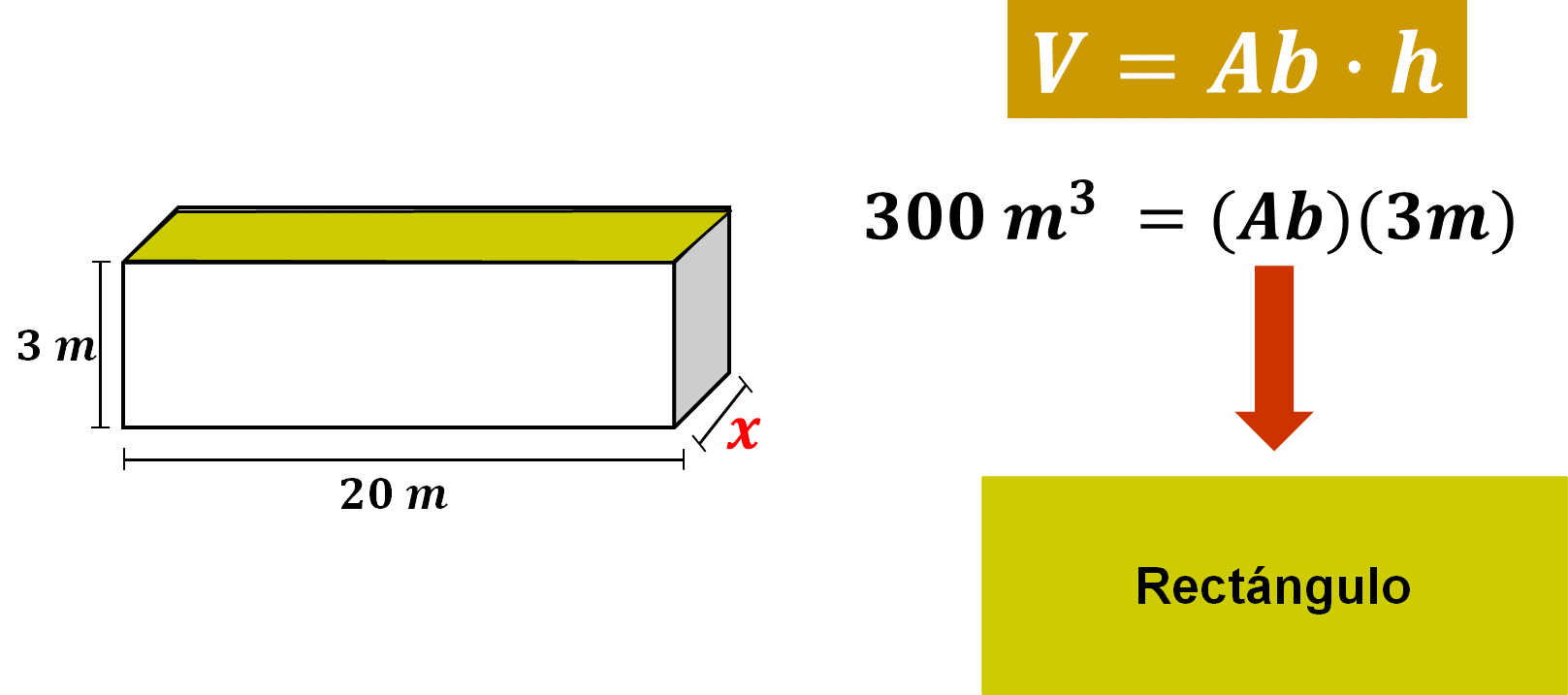
Para calcular parte de la información que necesitas para la solución, vas a sustituir los datos que conoces en la fórmula, para calcular el volumen de un prisma recto.

De esta manera, tienes que el volumen de la piscina de 300 metros cúbicos es igual al producto del área de la base por su altura, que es de 3 metros.

Nuevamente vas a realizar un despeje para dejar del lado izquierdo, del signo igual, los valores que conoces, y resuelve:

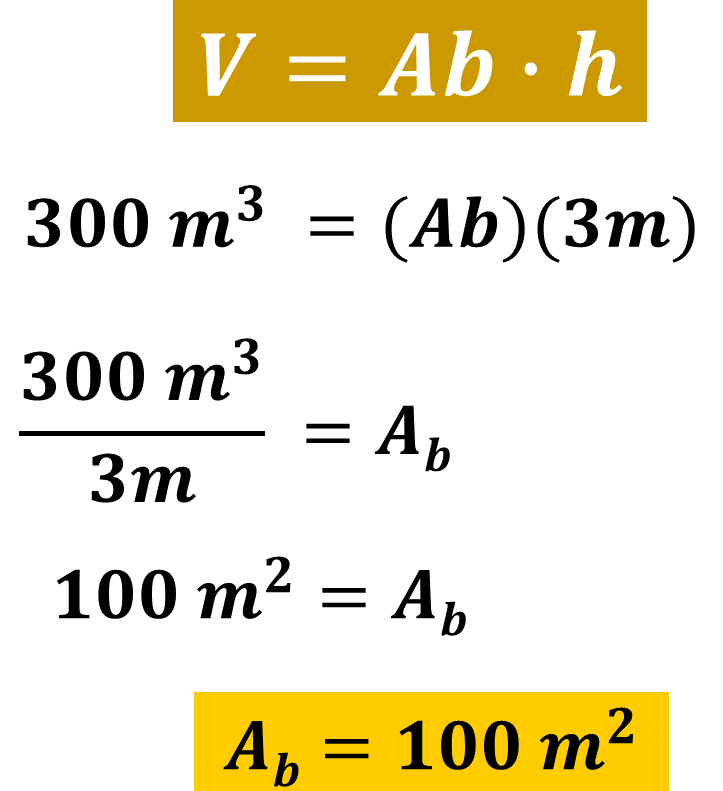
Por lo tanto, el área de la base de la piscina es igual a 100 metros cuadrados.

La información que obtuviste corresponde a la medida del área de la base. A partir de esta información es posible conocer las dimensiones del rectángulo de la base.

La fórmula para calcular el área de un rectángulo es igual a base por altura, o largo por ancho, de manera que, en la piscina de base rectangular, el largo mide 20 metros y el ancho “x” es la medida que se desconoce.

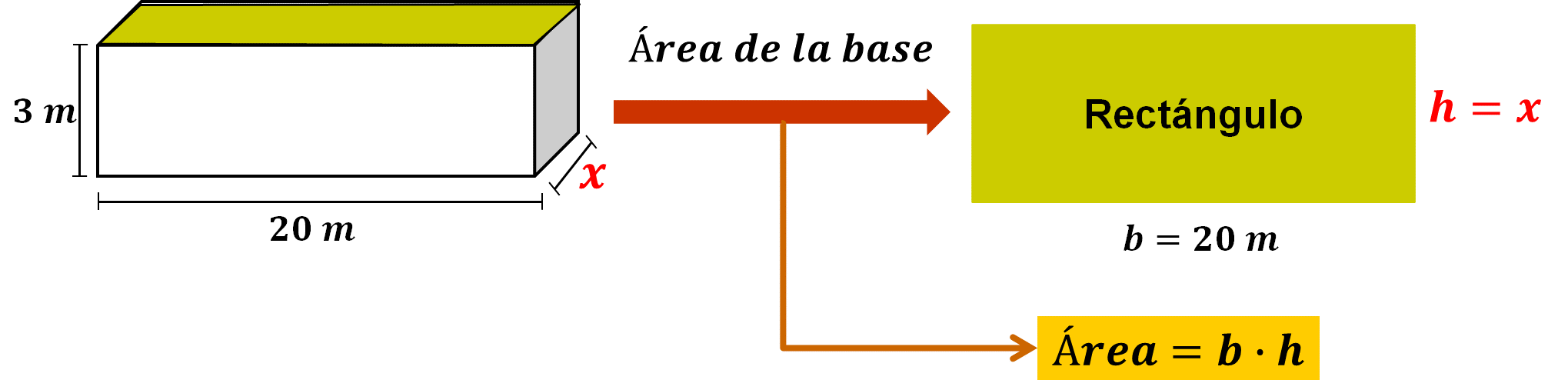
Entonces, puedes utilizar la fórmula para calcular el área de un rectángulo para encontrar la medida que se busca, si sustituyes los datos que conoces y luego realizas un despeje, de esta manera tienes que:

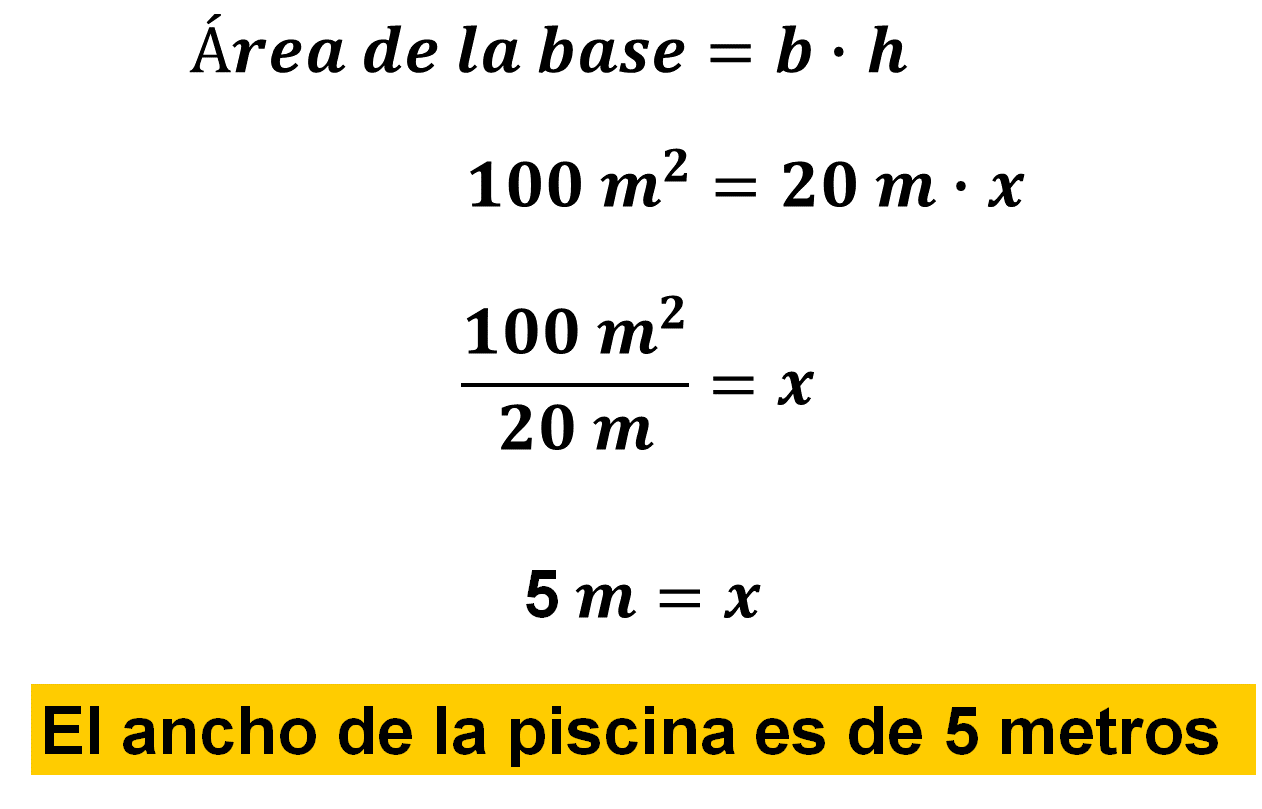
Por lo tanto, el resultado es 5 metros.

Eso quiere decir que la respuesta a la pregunta planteada es que 5 metros es la medida del ancho de la piscina.

El proceso fue más largo que en el problema anterior, debido a que la medida que se buscaba es parte de la figura de la base del prisma, pero si se busca calcular solamente el área de la base, bastará con que apliques la siguiente fórmula:

Para determinar el área de la base de un prisma recto, basta con dividir el volumen entre la altura del prisma.

Esta fórmula es la misma que se utiliza para resolver el problema de la piscina rectangular, pero debido a que la información solicitada era de una de las medidas del rectángulo de la base, se siguió un procedimiento adicional para calcular el resultado.

El volumen en Matemáticas se refiere al espacio tridimensional que ocupa un cuerpo geométrico.

Para obtener el volumen de prismas rectos se calcula el área de la base y el resultado se multiplica por la altura del prisma. Este cálculo se generaliza en la fórmula:

Volumen es igual al producto del área de la base por la altura

Cuando se conoce el volumen de un prisma y se desconoce alguna de sus dimensiones, puedes usar las siguientes expresiones:

Antes de realizar cualquier determinación es muy importante analizar las características del cuerpo geométrico, su forma y sus dimensiones.

El reto de hoy:

Revisa y practica lo aprendido en tu libro de Matemáticas de segundo grado. Resuelve los ejercicios que correspondan a este tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/