El método adecuado III
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
El método adecuado III
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas.
¿Qué vamos a aprender?
En esta sesión continuarás aprendiendo a resolver sistemas de dos ecuaciones lineales con dos incógnitas, ahora mediante el método más conveniente.
Ten a la mano tu cuaderno u hojas para tomar notas y tú lápiz o bolígrafo y una goma.
¿Qué hacemos?
Para fortalecer lo aprendido, ampliarás el conocimiento y se aclararán dudas. Asimismo, se precisarán algunos aspectos necesarios para resolver un sistema de dos ecuaciones lineales con dos incógnitas mediante el método más conveniente.
Has aprendido que los valores desconocidos de un sistema de dos ecuaciones lineales con dos incógnitas se pueden representar mediante las literales “x” y “y”, entre otras. El valor de cada una de las incógnitas, en este caso de “x” y de “y”, debe ser el mismo en ambas ecuaciones para que se cumplan las igualdades.

Recuerda que durante el ciclo escolar se han modelado situaciones mediante sistemas de dos ecuaciones lineales con dos incógnitas y resuelto esos sistemas empleando el método gráfico, el método de sustitución, el de igualación, así como el de suma y resta, algunos de los cuales se retomarán en esta sesión.
Se iniciará con la primera situación.
También sabes que debes plantear el sistema de ecuaciones lineales con dos incógnitas, con base en los datos identificados en el problema propuesto.
Revisa el siguiente problema:
La suma del cuádruple de un número y el cuádruple de otro es igual a 100; se sabe que el cuádruple del primero menos el cuádruple del segundo es igual a 60. ¿Cuáles son esos dos números?
Primero se plantea el sistema que representa al problema y así se obtiene el sistema:
4 “x” más 4 “y” igual a 100.
4 “x” menos 4 “y” igual a 60.
En donde “x” representa al primer número y “y” representa al segundo número.

Ya que tienes identificadas las incógnitas “x” y “y”, así como el sistema de ecuaciones lineales con dos incógnitas, a partir de este paso el procedimiento será diferente, ya que dependerá del método que elijas utilizar para la resolución de ese sistema.
¿Cuál método de resolución elegirías y por qué?
Toma notas de tus dudas y consúltalas con tu profesora o profesor, si te es posible.
Ahora, se resolverá un problema mediante el planteamiento de un sistema de dos ecuaciones lineales con dos incógnitas, y se decidirá cuál es el método más apropiado para determinar los valores de las incógnitas.
Piensa en la siguiente situación:
Se construye un cuadro con tiras de madera iguales. Se desconocen las medidas del largo y del ancho de esas tiras. Así que se le llamará “x” a la medida del largo y “y” a la del ancho.
Las tiras se acomodan como se muestra en la siguiente figura, se sabe que el perímetro del cuadrado exterior es de 100 centímetros y el del cuadrado interior de 60 centímetros. ¿Cuánto mide el largo de las tiras? ¿Y cuánto mide el ancho de las tiras?
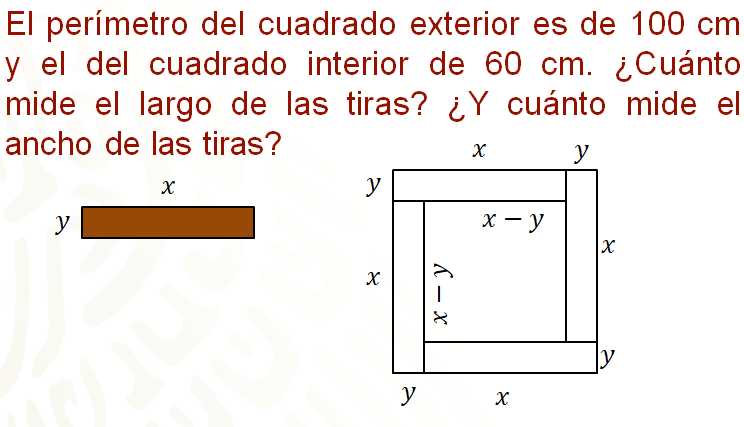
Una manera de iniciar la resolución del problema es responder primero la pregunta: ¿cuánto miden los lados del cuadrado exterior y cuánto los del interior?
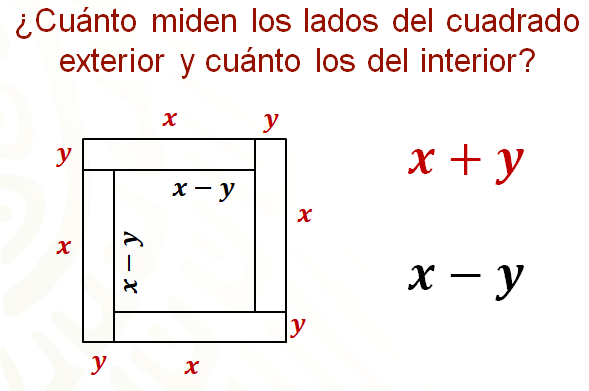
Seguramente, ya sabes cómo resolver el problema.
Al observar la figura, con las tiras de madera de “x” centímetros de largo y “y” centímetros de ancho, puedes ver que los lados del cuadrado exterior miden “x” más “y” y los del cuadrado interior “x” menos “y”.
¿Cómo representarías el perímetro de ambos cuadrados?
Como uno de los datos que se tienen es la medida del perímetro, tanto del cuadrado exterior como del interior, se tomará esa medida para plantear las ecuaciones del sistema. Recuerda que una manera de calcular el perímetro de un cuadrado es usando la fórmula perímetro igual a 4 por lado.
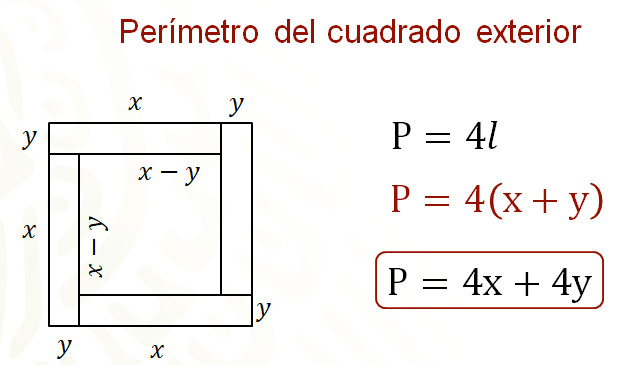
Al sustituir “x” más “y” en la fórmula tienes: perímetro igual a 4 por, abre paréntesis, “x” más “y”, cierra paréntesis. Entonces el perímetro es igual a 4 “x” más 4 “y”.
La expresión anterior representa el perímetro del cuadrado exterior.
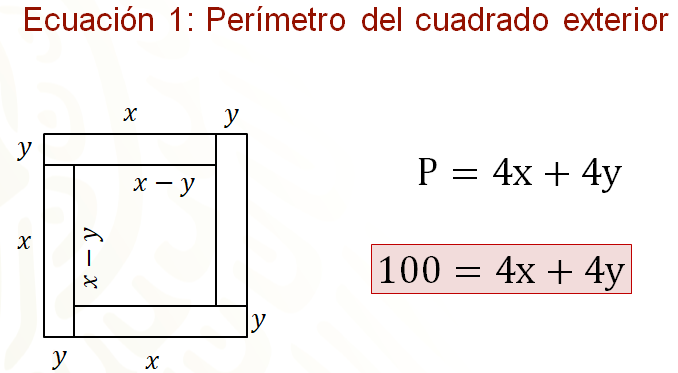
Recuerda que el perímetro del cuadrado exterior es de 100 centímetros; por lo tanto, la ecuación 1, que representa el perímetro del cuadrado exterior queda 100 igual a 4 “x” más 4 “y”.
Ahora, se va a representar el perímetro del cuadrado interior.
A partir de la fórmula para calcular el perímetro del cuadrado, que es perímetro igual a 4 por lado, se sustituye lo que representa el lado y se tiene que el perímetro es igual a 4 por, abre paréntesis, “x“ menos “y“, cierra paréntesis. Luego, perímetro igual a 4 “x“ menos 4 “y”.
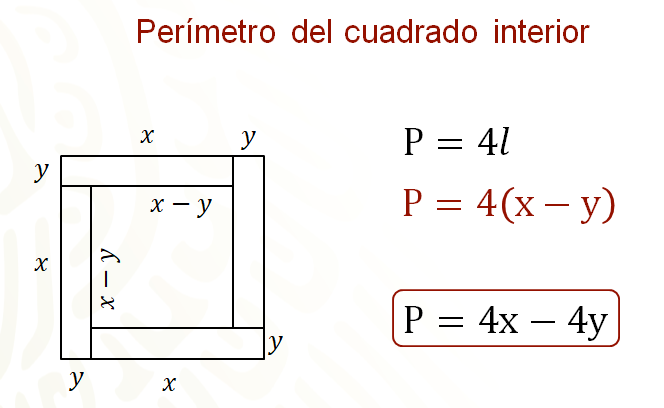
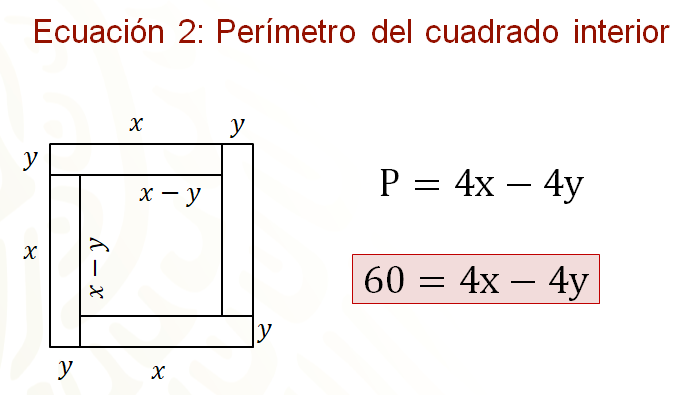
Entonces, esta expresión representa el perímetro del cuadrado interior, pero no olvides que el perímetro del cuadrado interior es de 60 centímetros, por lo tanto, la ecuación dos queda definida como 60 igual a 4 “x” menos 4 “y”.
¿Cuál es el sistema de ecuaciones que representa ambos perímetros?
Seguramente ya tienes la respuesta, compara, analiza y registra tus dudas e inquietudes para que las compartas con tu maestra o maestro de esta asignatura.
El sistema de dos ecuaciones lineales con dos incógnitas que permite resolver esta situación es: 4 “x” más 4 “y” igual a 100, que es la ecuación uno y 4 “x” menos 4 “y” igual a 60, que es la ecuación dos.

Ahora, se encontrarán los valores de “x” y “y” para saber las dimensiones de las tiras de madera que son los lados de los cuadrados.
¿Qué método utilizarías para resolver el sistema de ecuaciones? ¿Por qué?
Al observar las ecuaciones puedes darte cuenta de que la variable “y” tiene coeficientes simétricos, por lo que se puede eliminar rápidamente dado que su suma es cero. De acuerdo con lo anterior, se puede decir que el método más conveniente para resolver este sistema es el de suma y resta.
Una vez decidido este método para resolver el sistema, se suma la ecuación uno más la ecuación dos, de donde se tiene 4 “x” más 4 “x” igual a 8 “x”; 4 “y” menos 4 “y” igual a cero; 100 más 60 igual a 160. De esta manera se obtiene la ecuación 8 “x” igual a 160.

Ahora, divides ambos miembros de la ecuación entre 8 para obtener 1 como coeficiente de “x”. Por lo tanto, tienes 8 “x” entre 8 igual a 160 entre 8. De esto se obtiene que “x” es igual a 20.
¿Recuerdas qué representa “x” en esta situación?
“x” representa la medida del largo de las tiras de madera con que se formó el cuadrado.
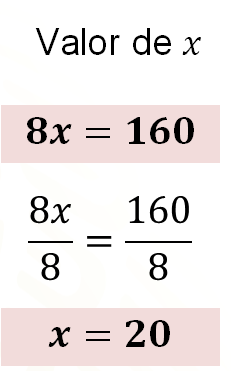
Ahora, puedes sustituir el valor de “x” igual a 20 en cualquiera de las ecuaciones originales. Se hará en la ecuación 1, que es 4 “x” más 4 “y” igual a 100. De donde se obtiene la expresión 4 por 20 más 4 “y” igual a 100.
Como 4 por 20 es igual a 80 se tiene 80 más 4 “y” igual a 100. Ahora suma el inverso aditivo de 80 en ambos miembros de la ecuación, de donde se obtiene 80 negativo más 80, más 4 “y” igual a 100 más 80 negativo. De lo anterior se obtiene 4 “y” igual a 20. Luego, divides ambos miembros de la ecuación entre el coeficiente de “y” que es 4; por lo tanto, ahora se tiene “y” igual a 5.
¿Recuerdas qué representa “y” en esta situación?
“y” representa la medida del ancho de las tiras de madera con que se formó el cuadro.

Ahora, se determinará si los valores obtenidos para “x” y “y” son correctos. Para ello, se sustituyen los valores de “x” y “y”, en la ecuación 1, que es 4 “x” más 4 “y” igual a 100, quedando 4 por 20 más 4 por 5 igual a 100. De acuerdo con la jerarquía de las operaciones, primero se resuelven las multiplicaciones, por lo que se obtiene 80 más 20 igual a 100. Al sumar 80 más 20 se obtiene 100; por lo tanto, se obtiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación 1.
Para la ecuación 2 se tiene 4 “x” menos 4 “y” igual a 60, se sustituyen los valores de “x” y “y” quedando 4 por 20 menos 4 por 5 igual a 60. De esto se obtiene 80 menos 20 igual a 60. Al restar 80 menos 20 se obtiene 60; por lo tanto, también se obtiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación 2; es decir, los valores de “x” y “y” son correctos.

Para finalizar esta situación, recuerda que el largo de las tiras fue representado por “x” y el ancho por “y”.
Ahora, responde las preguntas:
¿Cuánto mide el largo de las tiras?
Se puede afirmar que el largo de las tiras mide de 20 centímetros.
¿Cuánto mide el ancho de las tiras?
El ancho de las tiras mide 5 centímetros.

Se ha resuelto el sistema de dos ecuaciones lineales con dos incógnitas, usando el método de suma y resta. Pero ¿qué hizo que se tomará la decisión de utilizar este método y no otro?
Por lo que se decidió utilizar este método es que una de las incógnitas, en este caso “y”, tiene coeficientes simétricos en las ecuaciones originales, lo que permitió eliminarlas al sumar ambas ecuaciones para obtener una ecuación con una incógnita.
De manera general, se puede decir que para aplicar el método de suma y resta al resolver un sistema de dos ecuaciones lineales con dos incógnitas es necesario ver si alguna de esas incógnitas tiene coeficientes simétricos, o realizar cálculos para que esto ocurra.
Ahora, hay que resolver otra situación problema.
Se tienen dos cartulinas rectangulares con las dimensiones que se muestran en las siguientes figuras.
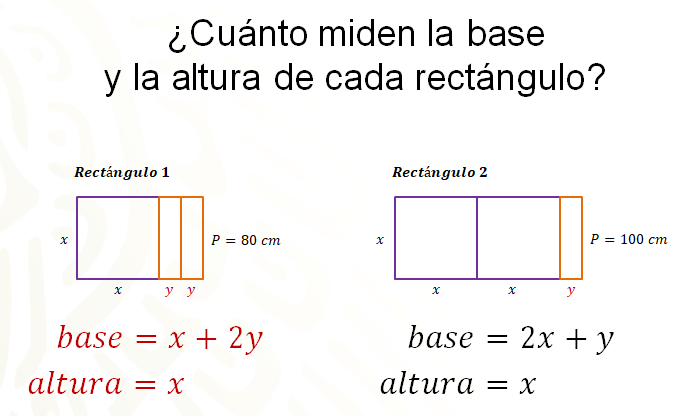
Si el perímetro de la primera es de 80 centímetros y el de la segunda es de 100 centímetros, ¿cuánto miden la base y la altura de cada rectángulo?
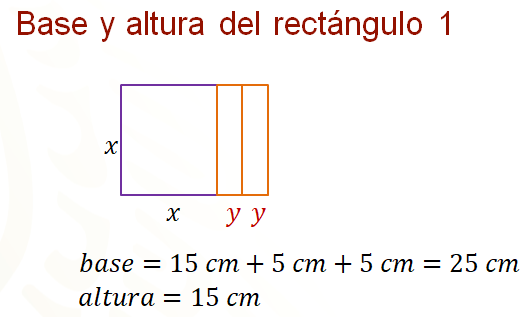
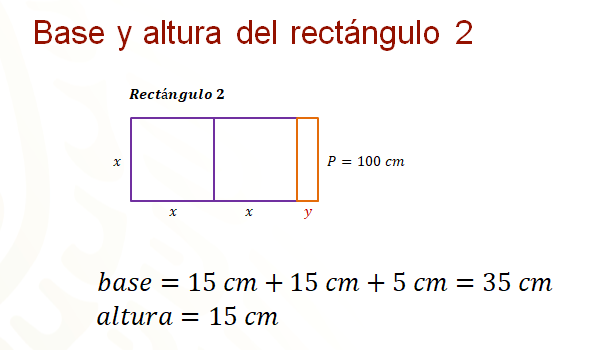
Por el momento, al observar las figuras sabes que la base del rectángulo 1 es igual a “x” más 2 “y” y su altura es igual a “x” para el rectángulo 2, la base es igual a 2 “x” más “y” y su altura es igual “x”.
Ahora, se representará algebraicamente el perímetro de cada rectángulo.
Primero, se hará la representación algebraica del perímetro del rectángulo 1. Utiliza la fórmula de perímetro igual a 2 por base más 2 por altura.
Entonces, el perímetro es igual a 2 por, abre paréntesis, “x” más 2 “y”, se cierra paréntesis, más 2 por “x”.
De esto se obtiene que el perímetro es igual a 2 “x” más 4 “y”, más 2 “x”, y al reducir términos semejantes el perímetro del rectángulo 1 es igual a 4 “x” más 4 “y”.

Como sabes que el perímetro de esta figura es de 80 centímetros; entonces, la ecuación uno del sistema, que te ayudará a encontrar las dimensiones de las figuras, queda definida como 4 “x” más 4 “y” igual a 80.

Ahora, la representación algebraica del perímetro del rectángulo 2 queda como perímetro igual a 2 por, abre paréntesis, 2 “x” más “y”, se cierra paréntesis, más 2 por “x”. De aquí se obtiene que perímetro es igual a 4 “x” más 2 “y” más 2 “x”. Luego, reduciendo términos semejantes, se obtiene que el perímetro del rectángulo 2 es igual a 6 “x” más 2 “y”.

Como sabes que el perímetro de esta figura es de 100 centímetros; entonces, la ecuación dos del sistema, que te ayudará a encontrar las dimensiones de las figuras, queda definida como 6 “x” más 2 “y” igual a 100.
Pero, ¿cuál es el sistema de ecuaciones que representa ambos perímetros?

Seguramente ya tienes la respuesta. Compara y analiza tus respuestas, registra tus dudas e inquietudes para que las compartas con tu maestra o maestro.
El sistema de dos ecuaciones lineales con dos incógnitas que permite resolver esta situación es: 4 “x” más 4 “y” igual a 80, que es la ecuación 1, y 6 “x” más 2 “y” igual a 100 que corresponde a la ecuación 2.

Ahora, hay que encontrar los valores de “x” y “y” para saber las dimensiones de los rectángulos.
Para ello, ¿qué método utilizarías para resolver el sistema de ecuaciones? ¿Por qué?
Recuerda que algo a considerar para elegir el método con el cual resolver un sistema de dos ecuaciones lineales con dos incógnitas es observar las características de las ecuaciones para decidir lo que puedes hacer.
En este sistema, por ejemplo, se puede observar que todos los términos, en ambas ecuaciones, son múltiplos del menor coeficiente que aparece en cada una de ellas.
Para la ecuación 1, todos los términos son múltiplos de 4, que es el coeficiente menor y que corresponde a “x” y a “y”. En el caso de la ecuación 2, todos los términos son múltiplos de 2, que es el coeficiente menor, y que corresponde a “y”. Por ello, al despejar la incógnita con el coeficiente menor, en este caso “y”, en esas ecuaciones se tendría una igualdad con coeficientes enteros, lo que facilitaría los cálculos.
Considerando lo anterior, ahora se elegirá el método de igualación en el que se debe despejar la misma incógnita en ambas ecuaciones para luego igualar las expresiones obtenidas en esos despejes. Entonces, despejando “y” en ecuación 1 se tiene que 4 “x” más 4 “y” igual a 80, sumas el inverso aditivo de 4 “x” en ambos miembros de la ecuación. Al operar se obtiene 4 “y” igual a 80 menos 4 “x”. Luego, se dividen ambos miembros de la ecuación entre el coeficiente de “y” que es 4, de donde se obtiene “y” igual a “x” negativa más 20.

Ahora, despejando “y” en la ecuación 2, que es 6 “x” más 2 “y” igual a 100, se suma el inverso aditivo de 6 “x” en ambos miembros de la ecuación y se reducen los términos semejantes, por lo que se obtiene 2 “y” igual a 100 menos 6 “x”. Luego, divides ambos miembros de la ecuación entre el coeficiente de “y”, que es 2, por lo que se obtiene “y” igual a 3 “x” negativa más 50.

Ahora, se debe igualar lo obtenido en los despejes de “y”, por lo que se tiene “x” negativa más 20 igual a 3 “x” negativa más 50.
Aplicando la transposición de términos, es decir, la manipulación algebraica para despejar la incógnita se obtiene “x” negativa más 3 “x” igual a 50 menos 20. De donde se obtiene 2 “x” igual a 30.
Ahora, se dividen ambos miembros de la ecuación entre el coeficiente de “x” que es 2, por lo que se obtiene que “x” es igual a 15.

Ahora, sustituyendo el valor de “x” en la expresión “y” igual a “x” negativa más 20, que es una igualdad obtenida de la ecuación 1, se tiene que “y” es igual al simétrico de 15, más 20, por lo que “y” es igual a 5.

Por lo tanto, el valor de “x” es igual a 15 y el valor de “y” es igual a 5.
Pero, ¿cómo puedes estar seguro de que esos valores son correctos?
Hay que comprobarlo, sustituyendo los valores en ambas ecuaciones.
En la ecuación uno, 4 “x” más 4 “y” igual a 80, se tiene 4 por 15 más, 4 por 5 igual a 80.
Al multiplicar obtienes 60 más 20 igual a (80). Sumando 60 más 20 se obtiene 80, por lo tanto, se tiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación uno.
Para la ecuación dos, 6 “x” más 2 “y” igual a 100, sustituyes los valores de “x” y “y”, ahora tienes 6 por 15 más 2 por 5 igual a 100. Luego de calcular los productos, la igualdad es 90 más 10 igual a 100.
Como 90 más 10 es igual a 100, se obtiene una identidad y se puede afirmar que los valores de “x” y “y” también hacen verdadera la ecuación dos, por lo tanto, se puede decir que los valores obtenidos para “x” y para “y” son correctos.

Siempre se recomienda hacer la comprobación en ambas ecuaciones para estar seguro de que los valores de “x” y “y” sean correctos.
Entonces, ¿cuánto miden la base y la altura de cada rectángulo?
Sustituyes los valores de “x” y de “y”, de manera que para el rectángulo 1, la base es igual a 15 centímetros más 5 centímetros, más 5 centímetros igual a 25 centímetros y la medida de la altura, que es igual a “x” es de 15 centímetros.
Para el rectángulo 2, la base es igual a 15 centímetros más 15 centímetros, más 5 centímetros. De donde se obtiene que la base mide 35 centímetros y la medida de la altura es de 15 centímetros.
Se ha resuelto la situación problema, registra tus dudas, inquietudes y dificultades que hayan surgido y no olvides compartirlas con tu profesora o profesor.
Ahora, se mostrarán tres sistemas de dos ecuaciones lineales con dos incógnitas para analizar cuál método sería más adecuado utilizar para resolverlos. Las cuales se presentan en la siguiente tabla, donde se debe colocar los sistemas de ecuaciones en la primera columna y el método más conveniente en la segunda.

Se iniciará con el sistema de ecuaciones formado por 4 “x” menos 2 “y” igual a cero y “y” igual a “x” más 3.
¿Qué método piensas que es el más adecuado para resolver este sistema?
Dado que en una ecuación ya se encuentra despejada la “y” puedes pensar que el método más conveniente para resolver este sistema es el método de sustitución.
Ahora, para el sistema formado por 3 “x” menos 2 “y” igual a 1 negativo y 8 “x” más “y” igual a , ¿qué método piensas que es el más adecuado para resolverlo?
Puedes pensar que el método de sustitución podría ser el más adecuado, y habría que despejar una de las incógnitas en una ecuación para sustituir su valor en la otra.
También se podría utilizar el método de suma y resta, y para aplicarlo podrías multiplicar una ecuación por un número que te arrojara una ecuación equivalente con un coeficiente simétrico en uno de los términos de la otra ecuación para la misma incógnita. Por ejemplo, se puede multiplicar por 2 la segunda ecuación.
Hay que revisar un tercer sistema. Se trata de “y” igual a “x” más 3 y “y” igual a “x” negativa más cinco. ¿Qué método utilizarías para resolverlo?
El método de igualación dado que en ambas ecuaciones se encuentra despejada la misma incógnita. Pero, también podrías utilizar el método de suma y resta porque se observa que los términos con “x” tienen coeficientes simétricos.
Por otro lado, se podría utilizar el método gráfico, dado que se pueden asignar valores a “x” y encontrar su correspondiente para “y”, lo que determinaría coordenadas que, al unirse, generan las rectas que son las gráficas asociadas a esas ecuaciones.
Como ves, un mismo sistema de dos ecuaciones lineales con dos incógnitas puede ser resuelto usando cualquier método, lo importante es observar las características de ese sistema para decidir qué método utilizar. También es importante considerar las habilidades de cada persona para decidir sobre el método más adecuado.
El reto de hoy:
Realiza las actividades de tu libro de texto, correspondientes a resolver problemas que implican la resolución de sistemas de dos ecuaciones lineales con dos incógnitas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion