El método adecuado II

El método adecuado II

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas.

¿Qué vamos a aprender?

En esta sesión profundizarás en el estudio de los métodos de solución de sistemas de dos ecuaciones lineales con dos incógnitas.

Analizarás las características del método de suma y resta, así como las del método de sustitución, con la finalidad de que reconozcas cuál de ellos es más conveniente para resolver un sistema de dos ecuaciones lineales con dos incógnitas, también llamado de 2 por 2.

¿Qué hacemos?

Comienza con el siguiente sistema de 2 ecuaciones lineales con 2 incógnitas.

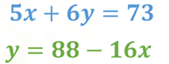
Observa que en la segunda ecuación la “y” está despejada, lo que podría hacerte pensar que el método de igualación podría ser el más conveniente para resolver este sistema de ecuaciones. Sin embargo, para resolverlo por el método de igualación tendrías que despejar la “y” en la primera ecuación e igualarlas. En esta ocasión, resolverás el sistema usando el método de sustitución y posteriormente analizarás qué método conviene usar.

Recuerda que para decidir qué método conviene más que otro depende de la apreciación personal, ya que puedes sentirte más segura o seguro resolviendo con un método, aunque tenga más pasos que otro.

En esta sesión, podrás fortalecer sus conocimientos y adquirir nuevas herramientas que te permitirán argumentar cuál es el método más conveniente para ti.

Muy bien, ahora, comienza a resolver el sistema por el método de sustitución. Como el nombre del método lo indica, tienes que realizar una sustitución. En este método se sustituye una incógnita por su valor y normalmente se comenzaría despejando una incógnita en cualquier ecuación. Observa que, en el sistema planteado, ya hay una incógnita despejada y es por eso se considera que el método de sustitución es más conveniente.

Así que, a partir del sistema planteado, comenzaremos sustituyendo el valor de “y”. Aunque en este momento no se sabe exactamente cuál es el valor de “y”.

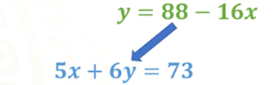
Entonces, la ecuación queda de la siguiente manera:

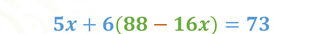
Observa que ahora tienes una ecuación con una sola incógnita, que es “x”. Por lo que, al resolver esta ecuación, estarás calculando el valor de “x”.

Siguiendo la jerarquía de operaciones, lo primero que harás es eliminar los paréntesis, pero dentro de ellos hay una sustracción que no se puede resolver, ya que en 88 menos 16 “x” no hay términos semejantes, así que, para eliminar los paréntesis, se aplica la propiedad distributiva de la multiplicación con respecto a la resta.

Haciendo uso de las propiedades de la igualdad, despeja “x” de la siguiente manera: Sustrae 528 en ambos miembros de la igualdad. Esto hace que la ecuación sea:

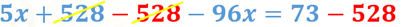
Posteriormente, reduce los términos semejantes, así, obtienes:

Ahora, divide ambos miembros por 91 negativo para tener el coeficiente uno para “x”. Con esto tienes:

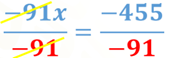
Al simplificar obtienes que el valor de “x” es igual a 5.

Una vez que se calcula el valor de una incógnita, se sustituye en alguno de los despejes o ecuaciones originales. Observa las ecuaciones originales en donde una de ellas ya tiene despejado el valor de “y”. ¿En cuál de ellas conviene sustituir el valor de “x”?

Como te habrás dado cuenta, conviene sustituir el valor en donde ya está despejada la “y”. Sin embargo, en esta ocasión sustituirás en ambas ecuaciones para que observes la diferencia.

Sustituyendo el valor de “x” igual a 5 en la primera ecuación tenemos:

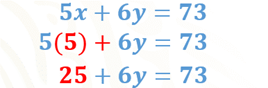
Resta 25 en ambos miembros de la igualdad.

Al reducir términos semejantes, obtienes:

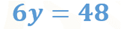
Finalmente, divide ambos miembros de la igualdad entre 6 para obtener uno como coeficiente de “y”.

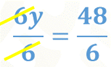
Así obtienes que:

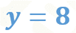
Ahora, si sustituyes el valor de “x” igual a 5 en la segunda ecuación, donde la “y” está despejada tienes:

Al resolver la multiplicación tienes:

Por lo tanto:

Puedes apreciar que, si sustituyes el valor obtenido para la primera incógnita, “x” = 5 en este caso, en la ecuación ya despejada puedes encontrar más rápido el valor de la otra incógnita, “y” en este sistema.

Para resolver este sistema de ecuaciones se eligió el método de sustitución porque una de las incógnitas ya se encontraba despejada en una ecuación.

Resuelve otro sistema de ecuaciones para continuar con esta sesión.

¿Qué te parece si ahora analizas el método de suma y resta?, y para ello trabajarás con el siguiente sistema de ecuaciones:

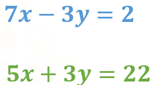
Responde las siguientes preguntas:

• ¿Tienes las coordenadas de los puntos por los que pasa cada una de las rectas que se generan al graficar las ecuaciones?
• ¿Las ecuaciones tienen la misma incógnita despejada?
• ¿Alguna de las ecuaciones tiene al menos una incógnita despejada?

Recuerda que si tuvieras las coordenadas de algunos puntos de las rectas que integran el sistema, podrías utilizar el método gráfico para resolver más rápidamente ese sistema de ecuaciones.

Si las ecuaciones estuvieran dadas de manera que se encontrara despejada la misma incógnita, entonces podrías aplicar el método de igualación como una forma más eficiente de resolución.

Si hubiera al menos una incógnita despejada, entonces podrías aplicar el método de sustitución eficientemente.

Pero, como para todas las preguntas anteriores, la respuesta es: no. Entonces ¿qué características tiene el sistema de ecuaciones y qué método te conviene usar?

Algo que puedes notar en este sistema es que en las ecuaciones que lo forman aparecen dos términos semejantes cuyos coeficientes son simétricos.

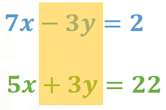
Por lo tanto, aprovecharás esta característica para resolver el sistema por el método de suma y resta, conocido también como método de reducción. Para ello trabajarás por columnas y realizarás las operaciones que cada uno de los términos indique. Es necesario que verifiques que en las columnas se encuentren términos semejantes.

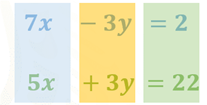
Por ejemplo, en el caso de la columna resaltada en color azul tienes los términos semejantes a “x”, en la columna resaltada en color amarillo están los términos semejantes a “y” y por último la columna resaltada en color verde tiene a los términos que no contienen a ninguna de las incógnitas.

Observa que en la columna de las “x” ambos términos son positivos, por lo que puedes establecer la operación 7x + 5x.

Para la columna de las “y” el término de la primera ecuación está restando y en la segunda se encuentra sumando, de ahí que puedes establecer la operación -3y + 3y.

En la última columna ambos términos son positivos, de donde puedes establecer la operación 2 + 22.

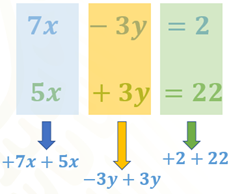
Al realizar las operaciones en cada columna obtenemos 3 resultados:

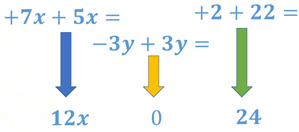
Con estos 3 resultados se forma una ecuación con una incógnita. La ecuación es:

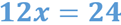
No se escribe el resultado de la reducción de la columna de las “y” porque resultó igual a cero.

Esta ecuación la puedes resolver de la siguiente manera: Haciendo uso de las propiedades de la igualdad divide ambos miembros de la ecuación entre 12, esto con la intención de obtener uno como coeficiente de “x”.

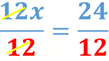
Por lo que tenemos que:

Ya que calculaste el valor de una incógnita, sustituirás este valor en cualquiera de las ecuaciones originales. Recordamos que en esta ocasión sustituirás el valor en ambas ecuaciones para que observes que llegarás al mismo resultado.

Al sustituir el valor de “x” igual a 2 en la primera ecuación obtienes:

Calculando el producto obtienes:

Luego, resta 14 en ambos lados de la igualdad y obtienes:

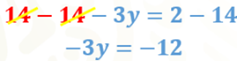
Por último, divide ambos miembros de la igualdad entre 3 negativo y con ello llegas al valor de “y”, que es igual a 4.

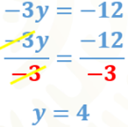
Para la segunda ecuación sustituirás el valor de “x” igual a 2 y tienes:

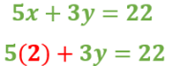
Calcula el producto y obtienes:

Luego, resta 10 en ambos lados de la ecuación y reduce términos semejantes. De donde obtendrás:

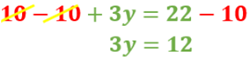
Posteriormente, divide ambos miembros de la ecuación entre 3 y al reducir obtendrás el valor de “y”.

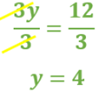
El sistema de ecuaciones 2 por 2, el cual comenzaste a resolver por el método de suma y resta, tiene un término 3 “y” que está restando en la primera ecuación y un término 3 “y” sumando en la segunda ecuación, ése fue el motivo principal por el cual se eligió resolverlo por dicho método.

Pero realiza otro ejemplo, en el cual también puede resultar útil emplear el método de suma y resta, aunque no se cumple la condición que viste en el ejemplo anterior. Este sistema está formado por las ecuaciones:

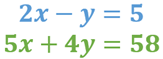
¿Estas ecuaciones tienen términos semejantes cuyos coeficientes sean simétricos, es decir, cuya suma sea cero?

Aunque no se cumple la condición anterior, puedes hacer una operación para lograr tener términos con coeficientes simétricos. Si multiplicas ambos miembros de la primera ecuación por 4, obtienes lo siguiente:

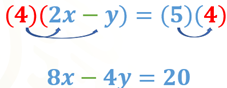
Coloca esta ecuación en lugar de la ecuación original del sistema. El nuevo sistema es:

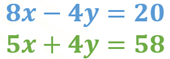
¿Observas alguna condición para elegir el método más adecuado para resolver el sistema de ecuaciones de 2 por 2?

Seguramente ya te disté cuenta de que en la primera ecuación tienes restando el 4 “y” y en la segunda ecuación está sumando el 4 “y”. Por lo cual, puedes resolver por el método de suma y resta, al que consideramos más adecuado dadas estas características del sistema.

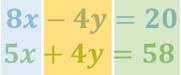
Para resolverlo considera los valores algebraicos por columnas. Ten siempre presente que, para trabajar por columnas, debes corroborar que éstas incluyan términos semejantes.

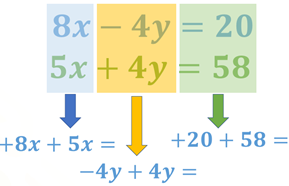
Para la primera columna hay un 8 “x” positivo y un 5 “x” positivo, los cuales al adicionarse resultan 13 “x”.

Para la segunda columna hay un 4 “y” restando y un 4 “y” sumando, por lo que, al adicionarse, se eliminan entre sí, dado que su suma es cero.

Para la tercera columna tenemos un 20 positivo y un 58 positivo, que al sumarse resulta en 78.

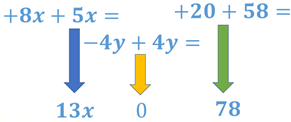
Ahora estos resultados que acabas de calcular, los integrarás en una nueva ecuación.

La nueva ecuación es:

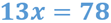
Para resolverla debes despejar a “x” y para ello es necesario dividir ambos miembros de la igualdad entre 13.

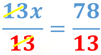
Al simplificar obtienes el valor de “x” que es:

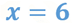
Como podrás darte cuenta, sólo tienes un valor conocido de las 2 incógnitas, por lo tanto, no has concluido su resolución, es necesario calcular el valor de “y” y para ello debes sustituir el valor que acabas de encontrar en alguna de las ecuaciones originales.

Sustituyendo el valor de “x” igual a 6 en la primera ecuación se obtiene:

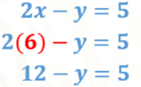
En la ecuación anterior, aplica las propiedades de la igualdad y resta 12 en ambos miembros de la ecuación, ahora tienes:

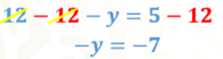
Para obtener el valor de “y”, multiplica ambos miembros de la ecuación por uno negativo. De esta manera al resolver las multiplicaciones lograrás encontrar el valor de “y”.

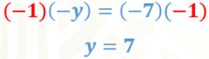
Ahora sustituye “x” igual a 6 en la segunda ecuación.

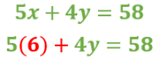
Al resolver la multiplicación tienes:

Haciendo uso de las propiedades de la igualdad, resta 30 en ambos miembros. Al resolver las sustracciones, la nueva ecuación es:

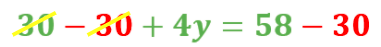
Para continuar divide ambos miembros de la igualdad entre 4 para despejar a “y”. De esta manera obtienes el valor de la segunda incógnita.

Hasta el momento has analizado 2 ejemplos donde el método de suma y resta es el más adecuado para resolver un sistema de ecuaciones lineales con dos incógnitas, agregaremos un tercer ejemplo:

¿Qué sucede si tienes un sistema de ecuaciones lineales con dos incógnitas donde:

¿Qué método elegirías como el más conveniente para resolver este sistema de ecuaciones?

Aparentemente, el método de suma y resta podría no ser la mejor opción para resolver este sistema de ecuaciones; sin embargo, dicho método sí es factible de aplicarse realizando algunas operaciones previamente.

Observa el siguiente video y analiza qué pasos siguen para resolverlo por el método de suma y resta.

1. Método de suma y resta, otra opción para resolver sistemas de ecuaciones

Del minuto 3:00 a 4:57

https://www.youtube.com/watch?time_continue=63&v=Q5Ym2jtN01Y&feature=emb_title

Como pudiste observar, se multiplicaron ambas ecuaciones, cada una por un número diferente, de manera que se tuvieran dos términos semejantes con coeficientes simétricos en ellas.

Ahora ya analizaste algunos métodos para resolver un sistema de ecuaciones de 2 por 2, por el método de sustitución y el método de suma y resta. Recuerda que el método más adecuado dependerá de las características del sistema de ecuaciones, pero influirá tu apreciación personal, dominio de cada uno de los métodos y el conocimiento que tengas acerca de las propiedades de la igualdad.

Recuerda que este es un material de apoyo y que, para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html