El jardín de Irma
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46Aprendizaje esperado: construye y usa una fórmula para calcular el perímetro de polígonos, ya sea como resultado de la suma de lados o como producto.
Énfasis: obtiene una fórmula para calcular el perímetro de polígonos regulares.
¿Qué vamos a aprender?
Aprenderás a obtener la fórmula para calcular el perímetro de polígonos regulares.
¿Qué hacemos?
Te quiero preguntar si te gustan los jardines y las hermosas flores con sus agradables aromas.
Me imagino que sí, además de que le dan vida a cualquier espacio donde se encuentren, ayudan al medio ambiente y hacen que cualquier lugar sea agradable.
Hoy te tengo una sorpresa que te encantará, esta clase va ser muy colorida e interesante, llena de una variedad de jardines de hermosos aromas y diferentes y complejas formas.
Hoy le vamos a ayudar a una de tus compañeras que se llama Irma, a saber cuánto material necesita para construir una jardinera.
Irma, la alumna de la que te comento, vive en el estado de Morelos que, por cierto, te digo un dato interesante del estado de Morelos, se considera a nivel mundial como el principal productor de flores ornamentales.
Ahora tenlo en cuenta por si llegas a visitar ese maravilloso estado, enmarcado con una gran variedad de las flores más bellas de México; siguiendo con el tema de la clase de hoy: Fíjate que me platica Irma, que le gusta visitar un lugar que se llama “Jardines de México, el paraíso de flores” ahí en Morelos, en donde se encuentran hermosos jardines temáticos, me cuenta que hay una gran variedad de flores y jardineras con diferentes formas.
Irma nos envió un video, donde se observan estos imponentes y hermosos jardines. Te invito a verlo del minuto 14:41 al 16:21
-
Jardines botánicos, santuarios de biodiversidad.
https://youtu.be/0wzKPIzmIAU?t=881
Realmente son espectaculares esos jardines botánicos de nuestro país, ahora comprendo porqué Irma quiere tener un jardín en su casa.
Le vamos a ayudar a Irma, para que pueda hacer un jardín parecido a los que vimos en el video.
Lo vamos a hacer en forma de un triángulo equilátero, por ese motivo ella sembró en su casa durante la contingencia diferentes tipos de flores, porque quiere hacer jardineras como las que observamos en el video, y para que las recordemos nos envió esta fotografía.

Irma me dijo que había sembrado dalias. Observa está fotografía que nos envió de las flores que cultivó.

Esta hermosa y colorida flor es endémica de México y es la flor representativa de nuestro país. Se cultiva en México desde la época de los mexicas quienes la cultivaron y reprodujeron hasta crear una gran diversidad que no sólo engalana nuestros jardines sino los jardines de varias partes del mundo, también es conocida con el nombre de acocoxóchitl, xicamiti o flor de camote, el 4 de agosto es el día nacional de la dalia.
Irma quiere utilizar tiras de madera para hacer su jardinera.
¿Cuánto mide su jardinera?
La siguiente figura representa las medidas de su jardinera, aquí vemos que cada uno de sus lados mide 3 metros.
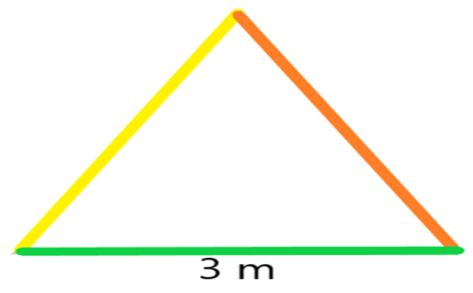
Entonces lo que se tiene que hacer es sumar cada una de las medidas de sus lados, para saber el total de metros de tiras de madera que va a utilizar, sumariamos lado más lado más lado, es decir 3 + 3 + 3 = 9 Irma necesitará 9 metros de madera para cada triángulo que quiera formar.
Si te fijas bien, lo que estamos calculando es el perímetro del triángulo; veamos cómo quedaría representado.
P = lado + lado + lado = 3 m + 3 m + 3 m = 9 m
Para calcular el perímetro del triángulo, tengo otra forma y sale lo mismo.
Como los tres lados son iguales, en lugar de una suma podríamos hacer una multiplicación, 3 por la medida del lado, la jardinera de Irma sería 3m por 3 m y da lo mismo, 9 metros.
Podemos expresar el perímetro de un triángulo equilátero de cualquiera de esas dos formas y llegaremos al mismo resultado. Ahora ya sabemos calcular el perímetro de un triángulo equilátero.
¿Cómo calculamos el perímetro de cualquier otra figura?
R = Sumando las longitudes de todos sus lados.
Para calcular el perímetro de cualquier figura, ¿Siempre podrás sustituir la suma por una multiplicación?
Si te presento un triángulo como el siguiente, ¿Cómo calcularías su perímetro?

Una forma es sumando las medidas de sus tres lados: 8 metros, más 6 metros, más 5 metros, nos da 19 metros.
En este caso no podemos hacer una multiplicación, porque ninguno de los lados es igual.
La multiplicación se puede usar para calcular el perímetro cuando los lados de la figura tienen la misma medida, como una forma de sintetizar la suma, pero si la medida de sus lados es diferente, entonces solamente nos queda sumarlos para obtener el perímetro.
Sólo en las figuras como la del jardín de Irma que tienen sus lados iguales se puede sustituir la suma por una multiplicación.
Le pudimos ayudar a Irma a calcular cuántos metros necesita para hacer su jardinera y además vimos dos formas diferentes de hacer el cálculo.
Recuerda que una figura es regular cuando todos sus lados tienen la misma medida y todos sus ángulos miden lo mismo, por eso se llaman figuras regulares y cuando no se cumple esto, se dice que las figuras son irregulares, como el segundo triángulo que te mostré donde todos sus lados tienen diferente medida.
Ahora vamos a resolver el desafío número 70 “Hagámoslo más fácil”, que se encuentra en la página 131 de tu libro de Desafíos Matemáticos.
Ahora dime, ¿Qué observas en las figuras del desafío?
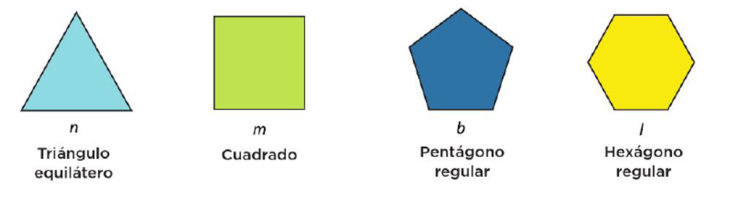
Que nos presentan un triángulo equilátero, y por lo tanto es una figura regular, porque esos triángulos tienen la misma medida de sus lados y de sus ángulos.
Ahora dime si el cuadrado será una figura regular.
Sí, porque los cuadrados tienen sus 4 lados iguales y también sus ángulos miden lo mismo.
Las figuras que no tienen sus lados y ángulos iguales, se llaman figuras irregulares. Pero como ves, las dos figuras siguientes tienen abajo su nombre y dice que son regulares.
Resuelve con nosotros los problemas y al final compara tus resultados con los que obtengamos.
-
El triángulo equilátero representa un jardín cuyos lados miden 6 m cada uno, y alrededor de él se va a colocar una cenefa de adoquín. ¿Cuántos metros de adoquín será necesario comprar?
Como la figura es un triángulo equilátero tiene sus tres lados iguales y mide seis metros, entonces podemos sumar 6 m + 6 m + 6 m o también podemos multiplicar 3 x 6 m y de las dos formas llegamos a que se necesitan 18 metros de adoquín.
Lado = 6 m
P = lado + lado + lado
P = 6 m + 6 m + 6 m = 18 m
P = 3 x 6 m = 18 m
P = 18 m
Continuemos con el siguiente problema y dice así:
-
Si el jardín tuviera forma cuadrada, como el segundo dibujo, y cada lado midiera 4.7 m ¿Qué cantidad de adoquín sería necesaria?
Como la figura es un cuadrado tiene sus cuatro lados iguales y cada uno de sus lados mide cuatro puntos siete metros, entonces a mí se me hizo más fácil multiplicar de esta forma:
Lado = 4.7 m
P = 4 x lado
P = 4 x 4.7 = 18.8 m
Lo hiciste multiplicando la medida de un lado por los 4 lados que tiene el cuadrado.
Por último vamos a resolver el siguiente problema:
-
Si para un jardín de forma hexagonal, representando por la última figura, se utilizaron 21 m de adoquín, ¿Cuánto mide cada uno de sus lados?
Ahora tenemos que pensarle más, porque para resolverlo no podemos utilizar la multiplicación ni la suma, porque no nos piden el perímetro, sino que nos piden la medida del lado, ahora es al revés.
Si no podemos utilizar la multiplicación, entonces podemos utilizar lo inverso a ella que es una división.
Como la figura es un hexágono regular entonces sus seis lados son iguales, si nos están dando la medida del perímetro que es 21 m, lo que debemos hacer es dividir el perímetro entre la cantidad de lados que tiene la figura:
P = 21 m
Lado = 21 ÷ 6 = 3.5 m
Lado = 3.5 m
Te invito a observar el siguiente video, donde aprenderás como puedes hacer tu propio jardín.
-
Creación de un jardín a partir de la obra "Cara de bolsa”.
https://www.youtube.com/watch?v=dylbPuOrvc0
Vamos a repasar las fórmulas para calcular el perímetro de cada una de las figuras que representan los jardines.
La fórmula del triángulo equilátero es: perímetro es igual a tres veces lado o 3 por lado, que es igual a lado, más lado, más lado.
La fórmula del cuadrado es: perímetro es igual a cuatro veces el lado, que es igual a lado, más lado, más lado, más lado, o P = 4 x lado.
La fórmula del pentágono regular es: perímetro es igual a cinco veces su lado, que es igual a lado, más lado, más lado, más lado, más lado, o P = 5 x lado.
La fórmula del hexágono regular es: perímetro es igual a seis veces el lado, que es igual a lado, más lado, más lado, más lado, más lado, más lado, o P = 6 x lado.
Te invito a comparar tus resultados con los que obtuvimos en la clase.
En la sesión de hoy aprendimos cómo hacer un pequeño jardín, además de ayudar a Irma a calcular el material que necesita para su jardinera, también conocimos información muy interesante sobre uno de los jardines más hermosos en México, y obtuvimos las fórmulas para calcular el perímetro de figuras regulares.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P5DMA.htm
Descarga tu clase dando clic aquí




Login to join the discussion