Ecuaciones y funciones

Ecuaciones y funciones

Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.

Énfasis: diferenciar entre ecuaciones y funciones.

¿Qué vamos a aprender? 

Lo que vas a necesitar para esta clase será: cuaderno, lápiz y tu libro de texto.

Anota las dudas, inquietudes o dificultades que surjan al resolver los planteamientos dados.

Ya has trabajado con ecuaciones y funciones. Cuando observas una expresión algebraica ¿puedes distinguirla?

¿Qué hacemos?

Para establecer la diferencia entre ecuación y función, define cada uno de sus conceptos.

Una ecuación es:

Una función se define como:

¿Por qué se les llama variable dependiente e independiente?

La variable dependiente es aquella cuyo valor depende del valor numérico de la variable independiente.

Y entonces, la variable independiente es la que no depende de ninguna otra sino, sus valores son los datos del problema.

La nomenclatura utilizada en las funciones es:

y= o f(x) =

Por ejemplo, si necesito expresar la relación entre un número y el triple de este mismo puedes usar:

y= 3x o f(x)= 3x

Llenar tablas tiene que ver con que toda función se puede representar a través de una gráfica, una tabla o través de una ecuación.

Y para completar las tablas, así como cuando requieres calcular el valor de un dato de una función, lo que haces es sustituir éste en la expresión de la función. Por ejemplo:

Si tienes la función

y=f(x)=12x

Y quieres saber el valor de la variable dependiente en la función, por ejemplo, cuando x es igual a 15, lo que harás es sustituir en la expresión del siguiente modo,

f(15)=12(15)

f(15)= 180

Esto quiere decir que para el valor de x=15, el valor de f(x) es igual a 180

De este modo, calcula el valor de la variable dependiente en la función, realizando las operaciones que corresponden a la expresión algebraica que la representa.

Entonces, esto es una función.

Con sólo los conceptos de ecuación y función puede que no esté clara la diferencia entre ambos, así que analizarás algunos ejemplos:

Situación 1:

La mamá de Joaquín tiene una papelería que tiene una alta demanda, ya que saca fotocopias de calidad. Ella requiere tener en el mostrador, una lista que le ayude rápidamente a saber cuánto debe cobrar a sus clientes.

Su hijo, Joaquín, se decide a hacerla y recuerda que en su clase de matemáticas ha realizado alguna vez una tabla de datos de una función matemática.

Joaquín pone manos a la obra y realiza la tabla considerando que cada fotocopia cuesta 60 centavos.

Observa esa tabla:

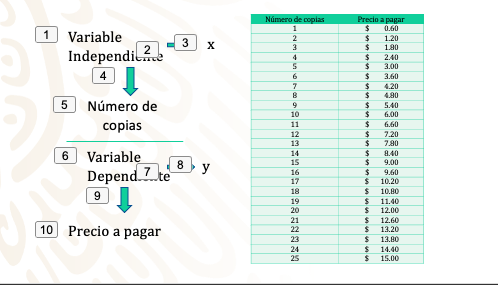
En la tabla, observas que el número de copias es la variable independiente y la variable dependiente es el precio a pagar. Joaquín multiplicó en todos los casos el número de copias por sesenta centavos y, en esas unidades, expresó los precios a pagar.

Así, a la primera columna la denominamos “x”, que es la variable independiente, pues el número de copias es algo a elegir de manera personal, y a la segunda columna la denominamos “y=f(x)” que corresponde a la variable dependiente, pues cada valor de ella es el resultado de multiplicar el valor asociado de x según corresponde.

En esta tabla, Joaquín ha seguido la función.

f(x)=0.60x

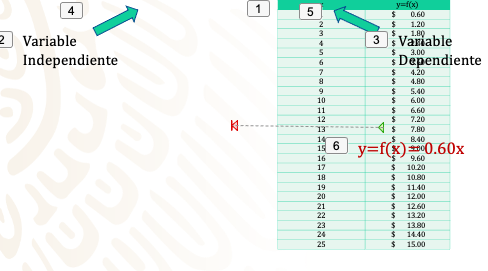
Joaquín sólo multiplicó el número de copias por sesenta centavos de cada una, pero ¿qué pasa si, por ejemplo, un cliente llega y le dice quiero, 100 pesos de fotocopias?

En ese caso también se puede calcular.

Observa qué pasó cuando la mamá de Joaquín tuvo que fotocopiar varios legajos de hojas. El cliente ya le dejó pagado el trabajo, pero ella no estaba en ese momento. Sólo sabe que el total es de 308.40 pesos.

Ella recurre a Joaquín, quien rápidamente le dice que averiguara cuántas fotocopias son y escribe la siguiente expresión matemática para ayudar a saber esto.

La expresión que escribe es:

0.60x=308.40

Lo cual le permitirá saber específicamente el caso planteado.

Resuelve:

0.60x=308.40

X= 308.40 entre 0.60

X= 514

Así, Joaquín al sustituir el dato conocido, formula una ecuación, misma que al resolverla, le permite saber que se trata de sacar 514 fotocopias.

En este segundo caso, Joaquín al tomar el valor del costo total de las fotocopias solicitadas, y sustituir ese valor en la función y= 0.60x convirtió la expresión en una ecuación.

Efectivamente. La convirtió, de ese modo, en una ecuación.

Por lo que:

308.40 = 0.60x dejó de ser una función.

Así la expresión f(x) =0.60x es una función, pues a cada valor de “x” le corresponderá un valor de “y”

Y la expresión 308.40=0.60x es una ecuación, pues el valor de “x” que cumple la igualdad es uno y sólo uno.

Una ecuación no acepta cualquier valor para la variable independiente “x” ya que es una incógnita con un valor único.

Con este ejemplo es posible darte cuenta de la diferencia entre una función y una ecuación.

Situación 2:

Omar tiene en sus manos la lista de consumo de gasolina de un vehículo de la empresa de su papá. La lista, de algún modo, quedó incompleta y ahora no puede sacar el gasto total de combustible del vehículo del mes pasado.

Es posible auxiliarse del rendimiento del vehículo, es decir, de la cantidad de kilómetros que recorre un auto por cada litro de gasolina.

Esa información se requiere, ya que existe una relación funcional entre la cantidad de combustible consumido y el número de kilómetros que recorre. Así que Omar investiga lo que corresponde al modelo y éste tiene un consumo promedio de 19.7 kilómetros por litro.

Observa la tabla que tiene Omar:

Como verás, quedan dos espacios incompletos en la tabla, uno para la semana 1 y otro en la semana 3.

Tomando en cuenta la relación entre la cantidad de combustible consumido y el número de kilómetros recorrido, Omar plantea la siguiente función:

km recorridos = Litros consumidos por rendimiento de combustible.

En este caso, debido a que los kilómetros por litro recorridos son 19.7, la expresión queda:

km recorridos =19.7 por litros

Si la variable independiente son los litros, “l” y la representas con “x” y la variable dependiente la representas con “y” que son los kilómetros recorridos.

Queda la expresión:

y=19.7 por x

Ahora, tomando en cuenta esta función ¿puedes completar la tabla para obtener los datos no conocidos?

Observa qué es lo que realiza.

Para el caso de la semana 1, Omar utiliza la expresión de la función y, al sustituir 630.4 en la variable “y”, deja la expresión 630.4 es igual a 19.7 por x, lo que la convierte en una ecuación que hay que calcular para saber el valor de “x”. En este caso, al ser una ecuación, “x” y “ye” dejan de ser variables y “x” pasa a ser una incógnita cuyo valor será único.

despejamos “x”

“x” es igual a 630.4 entre 19.7

“x” es igual a 32

Así, para la semana tres, se conocen los litros consumidos y sustituye en “x” 32.5.

“y” es igual a 19.7 por 32.5

Y, “y” es igual a 640.25

Ahora tiene completa la tabla correspondiente.

En este ejemplo puedes notar que los datos que Omar requería obtener no eran cantidades variables, sino incógnitas bien establecidas y cuyo valor era único, por lo que lo resolvió mediante un par de ecuaciones.

Efectivamente, y también puedes notar que la tabla, al estar completa, te permite ver la función matemática correspondiente, en donde a cada valor de la variable independiente, le corresponde uno y sólo un valor de la variable dependiente. También se realizan gráficas con las tablas de datos, es otra de las formas de representación de una función.

Observa ahora un ejemplo a partir de una gráfica.

Situación 3

Tienes el sistema de ecuaciones

x + y = 4

-x + y = -2

Es un sistema de ecuaciones lineales con dos incógnitas y lo resolverás por el método gráfico. Así que procederás a despejar a “y” en ambas ecuaciones.

En la primera, el despeje es:

y= 4 – x

En la segunda, el despeje es

y = x – 2

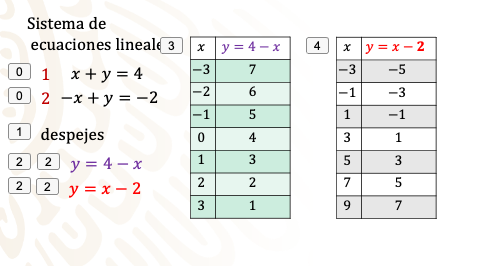
Asignas valores a “x” en ambas expresiones y calculas los valores de “y” para cada uno de ellos.

Así, tienes ahora las dos tablas. Una por cada ecuación del sistema y vas formando con ellas los pares ordenados (x,y)

Sí, ya sabes que en el plano cartesiano las coordenadas representan el recorrido de una distancia horizontal en el eje x y una distancia vertical en el eje y, todas a partir del origen (0,0).

Así, al graficar, puedes ver aquí dos rectas, cada una de ellas representa a la función que se tabuló y que fue originada por cada expresión algebraica que representa a cada ecuación del sistema original.

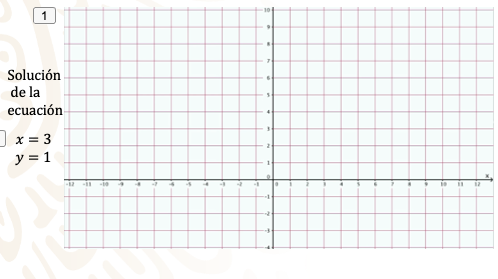
Observa que cada línea contiene en ella una infinidad de valores que asume la relación funcional en cuestión y que, a cada valor de “x”, le corresponde uno y sólo un valor de “y”.

Ahora, observa con detenimiento el punto de la coordenada (3,1) y verás que pertenece a ambas rectas. La intersección de las rectas que representan a cada ecuación es la solución del sistema de ecuaciones.

Así x=3 y y=1

¿Qué puedes concluir del ejemplo?

Que las funciones asumen una amplia cantidad de valores para las variables que la forman y las ecuaciones, en este caso, por ser de primer grado, asumen un único valor por incógnita.

Es decir, las rectas representan a las funciones que se derivaron de las ecuaciones, y el punto representa la unicidad de las soluciones de las incógnitas.

Y ¿siempre se tendrá esta situación? es decir ¿siempre las ecuaciones son funciones?

No, existen algunas ecuaciones que no son funciones. Observa una situación que te permita entender esto.

Situación 4

Graficarás a partir de la ecuación de una circunferencia. La ecuación que utilizarás es:

x^2+y^2 = 1

Que representa a una circunferencia de radio igual a 1. Colocas la expresión en tu programa de computadora y obtienes la gráfica correspondiente.

Observa que se ha graficado una circunferencia con centro en la coordenada (0,0) y radio igual a uno

Observa los siguientes puntos que pertenecen a la circunferencia.

(0.75, 0.66)

(0.75, -0.66)

(-0.5, -0.87)

(-0.5, 0.87)

Te das cuenta de que hay dos pares ordenados que tienen el mismo valor para “x”.

Efectivamente, sobre la circunferencia para el mismo valor de “x”, encuentras dos diferentes valores de “y”, lo que no es válido dentro de una función, ya que cada valor de la variable independiente debe tener uno y sólo un valor correspondiente en la variable dependiente, por lo que la expresión x^2+y^2=1 es una ecuación, pero no una función. Y esto es lo que se llama un contraejemplo.

Situación 5

Toma la expresión: y es igual a la raíz cuadrada de “x”

“”

Hay una situación que aclarar aquí.

Primero, observa ésta gráfica.

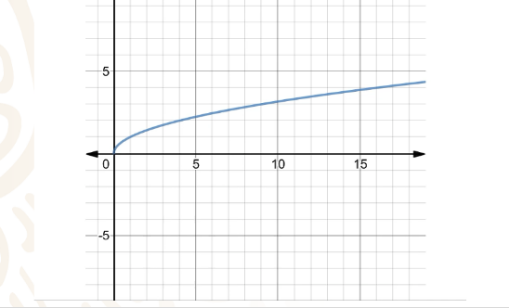
En ella, tienes una curva que representa a la raíz cuadrada. Puedes ver los puntos correspondientes a la raíz cuadrada de 1, que es igual a 1, a la raíz cuadrada de 4 que igual a 2, a la raíz cuadrada de 9 que es igual a 3 y a la raíz cuadrada de 16 que es igual a 4

Y si la analizas, podrás observar que a cada valor de la “x” le corresponde un sólo valor de “y”.

Bajo ese razonamiento, es una función, sólo que la gráfica te está mostrando sólo la parte positiva de la gráfica.

Entonces ¿qué falta tomar en cuenta?

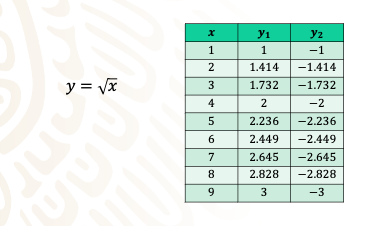
El considerar que la raíz cuadrada de un número tiene dos soluciones, ambas son simétricas entre sí. Elabora la tabla de valores de la expresión para aclarar esto.

Observa que, para cada valor de “x”, hay dos valores de “y”, mismos que estas representando en la tabla como “y” uno y “y” dos.

Eso no corresponde a una función.

Ahora, observa la gráfica de la curva incluyendo la sección negativa también.

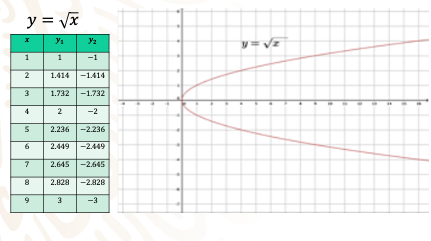
Con ello, se entiende que la expresión matemática anterior no es una función.

Situación 6

Resuelve gráficamente la ecuación x^2 -5x+4 =0

Se trata de una ecuación cuadrática y tiene dos soluciones para la incógnita.

Para resolverlo por el método gráfico, realiza la tabla de valores y obtén pares ordenados.

Transforma la expresión de la ecuación dada a la forma y=x^2-5x+4

En una hoja de cálculo, asigna valores para “x” en el rango de 3 negativo hasta 9 y calcula los valores correspondientes a “y”.

Posteriormente, coloca en el plano cartesiano los puntos de las coordenadas y observa que estos 12 puntos van formando la curva.

Une los puntos y forma la parábola que corresponde a la función. Ahora, recordando que la solución de la incógnita “x” se encuentran en el corte de dicha parábola con el eje de las abscisas, tienes que las soluciones de la ecuación solicitada se encuentran en los puntos (1,0) y (4,0) que pertenecen a la parábola.

Estos puntos los tienes en la tabla en donde “y” es igual a cero.

Las soluciones de la ecuación son “x” es igual a 1 y “x” es igual a 4. En este ejemplo, la función correspondiente a la ecuación que se resolvió, te ayuda a encontrar los valores de la incógnita, pues permiten ir construyendo la gráfica.

Y te da la posibilidad de ver que esta ecuación también es una función.

A modo de conclusión, tienes que:

El reto de hoy:

Te recomendamos completar tus notas de la sesión.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html