Ecuaciones lineales

Ecuaciones lineales

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.

Énfasis: resolver ecuaciones lineales de la forma ax + b = cx + d

¿Qué vamos a aprender?

En esta sesión te vas a inmergir al conocimiento para lograr el aprendizaje esperado:

Resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.

El propósito de la sesión es resolver ecuaciones lineales de la forma ax + b = cx + d.

Es muy importante tu participación en las actividades que se propondrá, por ello te recomiendo que lleves un registro de las ideas principales, las preguntas, retos y reflexiones que surjan.

Por lo mismo, te sugiero que tengas a la mano:

• Tu cuaderno de matemáticas u hojas blancas
• Un lápiz o una pluma
• Una goma
• Sacapuntas

También puedes tomar nota de los conocimientos más relevantes o de aquellos que te causen dudas para comunicarlos a tu maestra o maestro de asignatura, a distancia.

De igual manera, puedes poner en práctica lo aprendido durante esta sesión buscando ejercicios en tu libro de texto.

Esta sesión se planteará en tres partes. En la primera parte, enfatizarás aquellos aprendizajes necesarios para lograr el objetivo expuesto anteriormente; durante la segunda sección, generalizarás los procedimientos; y, por último, podrás en práctica lo aprendido a través de un reto.

¿Qué hacemos?

Seguramente en tu vida estudiantil llegaste a resolver ecuaciones lineales o de primer grado, llegaste a sumar, restar, multiplicar o dividir para encontrar el valor de una incógnita que era representada con alguna literal.

Durante esta sesión encontrarás el valor de esas incógnitas en una ecuación.

Recuerda que una ecuación es una igualdad en la que se relacionan datos conocidos y desconocidos, los cuales se representan con números, literales y operaciones aritméticas.

Un ejemplo de ecuación es: 5x +9 = 15x + 45, la cual está compuesta por dos miembros: los términos que se encuentran a la izquierda del signo igual conforman al primer miembro de la ecuación, mientras que los términos que se encuentran a la derecha forman el segundo miembro. Los valores que debes encontrar en una ecuación están representados por letras o literales, llamadas incógnitas. Los coeficientes son los números que acompañan a las incógnitas.

¿Puedes indicar en este ejemplo los coeficientes y los términos independientes o constantes?

En la ecuación 5x + 9 = 15x + 45, los coeficientes de las incógnitas son 5 y 15, mientras que los términos independientes o constantes están representados por 9 y 45.

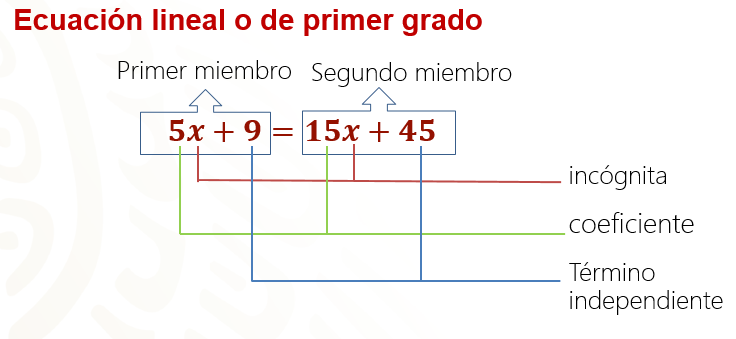
¿Qué ocurre cuando no hay un coeficiente o número que acompañe a la incógnita?

Eso quiere decir que el valor del coeficiente es igual a 1, pero no lo escribes porque todo número multiplicado por 1 es igual a sí mismo; entonces no es necesario colocarlo.

Otra cosa que necesitas para cumplir con los propósitos de esta sesión es reconocer las características que deben cumplir los términos semejantes para poder reducirlos al simplificar una ecuación.

Para identificar un término semejante a otro, ambos deben tener las mismas literales y el mismo exponente; recordando que, si el exponente no es visible o explícito, es porque es igual a uno.

Ésta es una tabla con términos algebraicos con determinadas características; hay otros términos, fuera de ella, que tienen características similares a los de la tabla.

En casa, ¿puedes identificar qué términos son semejantes entre sí?

En la primera columna se tiene el término “x” cuadrada y observa otro término que tiene el mismo exponente y la misma literal: 8x cuadrada.

En la siguiente columna se tiene el término “m” y su semejante es el término tres cuartos de “m”.

En el tercer ejemplo no hay literal, es el número 4 negativo; por lo tanto, el término semejante también será uno que no posea literal: 2.5 negativo

Por último, está 8x cúbica y su semejante es 21x cúbica negativo.

Ahora que ya sabes cómo identificar los términos semejantes, debes aplicar los procedimientos correspondientes para llevar a cabo una reducción o simplificación para que una ecuación quede expresada de manera más breve.

Para reducir los términos semejantes debes de tomar en cuenta el coeficiente que acompaña a la incógnita, incluyendo su signo; así, puedes sumar o restar, dependiendo del término, mientras que la literal y su exponente se quedan sin modificación alguna.

Aprovechando la tabla anterior, reduce los términos que ya identificaste como semejantes.

En la primera columna ambos términos son positivos; por lo tanto, debes sumar los coeficientes: 1 + 8 = 9; y, como las literales y su exponente no se modifican, el resultado es 9x cuadrada.

Para el siguiente ejemplo debes sumar 1 + 3/4, lo que es equivalente a un 1 entero 3/4 “m” o 1.75m.

Para el tercer ejemplo, no tienes literal y los números son negativos; por lo tanto, debes sumar 4 negativo más 2.5 negativo, lo que da 6.5 negativo.

Por último, se encuentran 8x cúbica más 21x cúbica negativa. En este caso, debes calcular la diferencia entre los valores absolutos y el resultado será un número negativo, porque 21 negativo tiene mayor valor absoluto que 8. Al operar, 21 menos 8 es igual a 13; entonces, quedaría 13x cúbica negativa.

También es muy importante tener en cuenta las ecuaciones equivalentes al resolver una ecuación.

¿Cuáles son las ecuaciones equivalentes?

Las ecuaciones equivalentes son aquellas expresiones equivalentes que poseen la misma solución y una se puede obtener a partir de las otras; para ello, puedes aplicar procedimientos que ya conoces relacionados con algunas propiedades de la igualdad.

¿Cómo puedes obtener las ecuaciones equivalentes?

En el siguiente ejemplo se tiene la ecuación x = 5, donde se sabe que el valor de la incógnita es 5, ya que al sustituir 5 en “x” se tiene que 5 es igual a 5, respetándose la igualdad.

Ahora, sumarás 10 en ambos lados de la igualdad, obteniendo la ecuación “x” + 10 = 5 + 10. Al simplificar el segundo miembro de la igualdad obtienes la ecuación x + 10 = 15.

Esta ecuación y la primera: x = 5 son ecuaciones equivalentes. Porque, si sustituyes a la incógnita por 5 en la ecuación, tienes que 5 + 10 = 15; por lo tanto, 15 = 15 y la igualdad se sigue cumpliendo.

De igual manera, se puedes multiplicar todos los términos de la segunda ecuación por 3, quedando de la siguiente manera: 3 (x + 10 = 15).

Al aplicar la propiedad distributiva queda la siguiente ecuación: 3x + 30 = 45. Para comprobar que esta ecuación es equivalente a la ecuación anterior, vas a sustituir nuevamente a la incógnita por 5; si la igualdad permanece, entonces estarás en lo correcto.

Al sustituir queda 3 (5) + 30 = 45. Al multiplicar 3 por 5 da 15 que, sumado a 30, es igual a 45; entonces la igualdad se ha cumplido 45 = 45.

Como 3x + 30 = 45 es una ecuación equivalente a x + 10 = 15, también es equivalente a x =5

Como verás, se tienen muchas formas de expresar una ecuación, mientras las expresiones sean equivalentes, la solución es la misma. En muchos casos, para llegar a la ecuación equivalente más simple se utilizan procedimientos recursivos al aplicar operaciones inversas. Para la suma es la resta; y para la multiplicación es la división.

Ahora ya tienes las herramientas necesarias, es hora de aplicar todos estos conocimientos en la resolución de un problema que implique una ecuación de la forma ax + b = cx + d

Observa la siguiente situación-problema.

Dos manzanas más 150 gramos tienen la misma masa que 3 peras, menos 90 gramos. Considerando que todas las frutas pesan lo mismo, ¿cuál es la masa de cada una?

Es una buena situación para comenzar. Pero ¿tienes alguna pista para poder establecer la ecuación del problema?

El problema dice que la masa de las frutas es la misma; por lo tanto, puedes saber que se refiere a la misma incógnita. De esta manera, puedes establecer una igualdad.

Recuerda que, para establecer la igualdad, es importante reconocer que se está hablando del mismo dato porque, de lo contrario, no se puede resolver dicha ecuación.

La incógnita en el problema sería la masa de las frutas, la cual se representará como la literal “m”.

Si tienes en el primer caso 2 manzanas, quedaría el termino 2 m y a las 3 peras las representarás como 3 m.

Para completar la ecuación debes de agregar o quitar la masa que se indica en el problema y que representa a los términos independientes.

Entonces, la expresión algebraica que represente la masa de las peras es 3 m menos 90, mientras que la expresión algebraica que representa a las manzanas es 2 m + 150. Ahora, sólo falta igualar ambas expresiones para obtener la ecuación. Al igualar las expresiones queda la ecuación: 3 m – 90 = 2m + 150.

Para resolver la ecuación lo primero que debes hacer es agrupar los términos semejantes del mismo lado de la igualdad.

Se dejará del lado izquierdo los términos con la incógnita, mientras que los términos independientes los dejaremos del lado derecho.

Para poder hacerlo utilizarás la propiedad uniforme de la igualdad.

Como a 90 lo antecede un signo menos, entonces tienes que sumar 90 en ambos lados y, como en 2m el coeficiente es positivo, entonces, restas 2m en ambos lados de la igualdad.

Así obtienes la ecuación 3 m – 90 + 90 – 2 m = 2 m + 150 + 90 – 2 m

Del lado izquierdo, 90 menos 90 es igual a cero y, del lado derecho, al restar 2 m menos 2 m también es cero. Así, eliminas esos términos del lado correspondiente y lo que queda la ecuación 3 m- 2 m = 150 +90.

¿Cuál sería el siguiente paso?

Ahora que ya tienes los términos semejantes agrupados del mismo lado de la igualdad, debes reducir para despejar a la incógnita. En este caso, restarás 3 m menos 2 m y sumarás 150 más 90 para obtener la ecuación m = 240, que representa la solución. Así, se sabe que cada fruta tiene una masa de 240 gramos, usando la consideración de que las manzanas y las peras tuvieran la misma masa.

¿Cómo te puedes asegurar que el resultado también es correcto?

Lo único que debes de hacer es sustituir la literal “m” por 240 en la ecuación inicial 3 m -90 =2 m + 150. A este procedimiento se le conoce como comprobación.

Entonces, al sustituir “m” por 240 queda de la siguiente manera: 3 por 240 menos 90 igual a 2, por 240 más 150. Ahora, para resolver, debes respetar la jerarquía de operaciones. Primero, realizarás la multiplicación y, posteriormente, las sumas y restas correspondientes.

Primero, multiplicas 3 por 240, que da como resultado 720; y 2 por 240 da como resultado 480. Al restar 720 menos 90 es igual a 630; y al sumar 480 más 150 da 630, también.

En ambos casos se obtuvo el mismo resultado.

De esta manera se comprueba que la igualdad se cumple, por lo que la solución de la ecuación es correcta.

Pareciera que se hicieron muchos procedimientos para llegar a la solución del problema.

Pero no fue así. Observa cada uno de los pasos que ayudan a generalizar el procedimiento para cualquier otro problema que implique resolver una ecuación.

Para resolver un problema por medio de una ecuación, primero analizas la información e identificas los datos del problema, para plantear la ecuación correspondiente; es decir, identificar los datos que se tienen y los que debes encontrar.

En el problema anterior, después de plantear la ecuación, el siguiente paso que realizas fue agrupar los términos semejantes.

Se agrupan términos semejantes: del mismo lado de la ecuación se colocan los términos con la incógnita, mientras que del otro lado de la ecuación se pasan los términos independientes o constantes.

El siguiente paso es reducir los términos semejantes.

En este paso se debes sumar o restar los términos.

En algunos casos, cuando el coeficiente de la incógnita no es uno, debes despejarla; esto quiere decir que cuando un coeficiente la multiplica se tiene que usar la operación inversa; es decir, dividir ambos lados de la ecuación entre ese número y, de esta manera, llegar a la solución.

Por último, debes de comprobar que los resultados sean correctos.

Recuerda que es importante verificar que el resultado sea correcto y esto lo lograrás sustituyendo el valor de la incógnita obtenida en la ecuación original. Si la igualdad se cumple, el valor encontrado de la incógnita es el correcto.

Entonces, de manera general, se puede decir que para la resolución de ecuaciones de la forma ax + b = cx + d.

Primero, se plantea la ecuación; en segundo lugar, se agrupan términos semejantes del mismo lado de la ecuación; en tercer lugar, se reducen los términos semejantes; en cuarto lugar, se despeja la incógnita y, por último, se comprueba la solución.

Ya debes de tener claro los pasos para resolver el tipo de ecuaciones vistas durante la sesión.

El reto de hoy:

Es momento de poner en práctica los aprendizajes de la sesión en un reto.

José trabaja en una empresa donde le dieron, como premio semanal, 8 cupones canjeables por mercancía en centros comerciales más 60 pesos. A Juan, que trabaja en la misma empresa, le dieron 2 cupones menos que a José, pero lo compensaron con 160 pesos. Los vales que les dieron a ambos trabajadores tienen el mismo valor, además de que la empresa afirma que se les dio la misma cantidad de dinero. Con esta información, ¿cuál es el valor de cada cupón?

¿Puedes descubrir si la afirmación de la empresa es correcta? ¿Cuánto dinero recibió cada uno?

En este caso, los cupones representarán a la incógnita y tienes que descubrir cuál es su valor.

Para plantear la ecuación, analiza los datos: José tiene 8 cupones más 60 pesos; al no saber el valor del cupón puedes interpretarlo con la literal “c”; por lo tanto, la expresión algebraica de la cantidad que recibió José quedaría como 8c + 60.

Juan recibió 2 cupones menos que José más 160 pesos; entonces, al restar 8c menos 2c da como resultado 6c; por lo tanto, la expresión algebraica para Juan quedaría 6c +160.

De ahí se obtiene la ecuación 8c + 60 = 6c + 160.

Al plantear la ecuación estas tomando como cierto que la empresa ha pagado lo mismo a ambos trabajadores.

La ecuación es: 8c + 60= 6c + 160

Como primer paso, debes agrupar los términos semejantes del mismo lado de la ecuación. En el primer miembro dejarás a los términos con las incógnitas; y en el segundo a los términos independientes o constantes.

¿Recuerdas qué tienes que hacer para que esto suceda?

Como del lado derecho se suman 60, entonces restas los mismos 60 en ambos lados y restas 6c en ambos lados, ya que es el valor de la incógnita del lado derecho.

Primero vas a restar 6c en ambos lados de la ecuación, aplicando la propiedad uniforme de la igualdad. Para obtener la ecuación 8c - 6c + 60 = 6c - 6c + 160, al restar 6c menos 6c, en el segundo miembro de la igualdad da cero; y, al simplificar el lado derecho, queda la ecuación: 2c + 60 = 160.

Ahora, restas 60 en ambos lados de la igualdad.

Al aplicar la propiedad de la igualdad y los métodos antes mencionados, obtienes la ecuación 2c + 60 – 60 = 160 – 60.

Al reducir los términos semejantes, obtienes la ecuación 2c = 100

Por último, se debe despejar la incógnita utilizando la operación inversa de la multiplicación; es decir, la división.

En este caso, vas a dividir toda la ecuación entre 2, ya que 2 es el coeficiente de la incógnita. Entonces, queda de esta manera: 2c entre 2 = 100 entre 2.

Al resolver las divisiones resulta que c = 50.

¿Qué preguntas puedes responder del problema planteado?

Puedes saber que el valor de cada cupón es de 50 pesos. Lo último que resta por averiguar es cuánto recibió cada uno. ¿Cómo crees que puedas corroborar la afirmación que hizo la empresa?

Puedes realizar la comprobación al sustituir el valor del cupón en la ecuación que inicialmente se planteó. Si al final queda la misma cantidad, puedeas responder la pregunta.

Se comienza sustituyendo la variable c por el valor que se adquirió del cupón; es decir, 50; por lo que te quedaría 8 por 50 + 60 = 6 por 50 + 160. Recuerda que, al resolver, debes aplicar la jerarquía de operaciones.

Entonces, multiplicas primero 8 por 50 y 6 por 50 para obtener los valores de 400 y 300. Para saber cuánto dinero recibió José suma 400 más 60 y para Juan será 300 más 160. La suma de los cupones más el dinero equivale a 460.

Se puede afirmar que, tanto Juan como José recibieron 460 pesos. Por lo tanto, la empresa pago la misma cantidad a ambos trabajadores.

Con la comprobación se ha dado solución al problema.

No olvides verificar tus resultados y expresar tus dudas a tu maestra o maestro de la asignatura, a la distancia.

¡Buen trabajo!

Gracias por tu esfuerzo. 

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html