División de números enteros
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06
Aprendizaje esperado: resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos .
Énfasis : d ar sentido y significado a la división de números enteros .
¿Qué vamos a aprender?
Profundizarás en diversos procedimiento s para la resolución de multiplicaciones y divisiones . En esta sesión, conocerás cómo dar sentido y significado a la división de números enteros, ya sean positivos o negativos .
¿Qué hacemos?
Para iniciar, analiza la siguiente situación.
Situación, tabla de multiplicar
Yan Carlo, que es un alumno de segundo grado de secundaria, tiene que encontrar los valores faltantes en una tabla de multiplicar que les dejó de tarea su maestra, pero tiene una duda.
Su hermana Valeria, quien es alumna de tercer grado, lo anima a resolver el reto; porque sabe que, en la clase de su hermano, ya vieron el tema de multiplicación de números enteros.
La tabla de multiplicar es la siguiente:
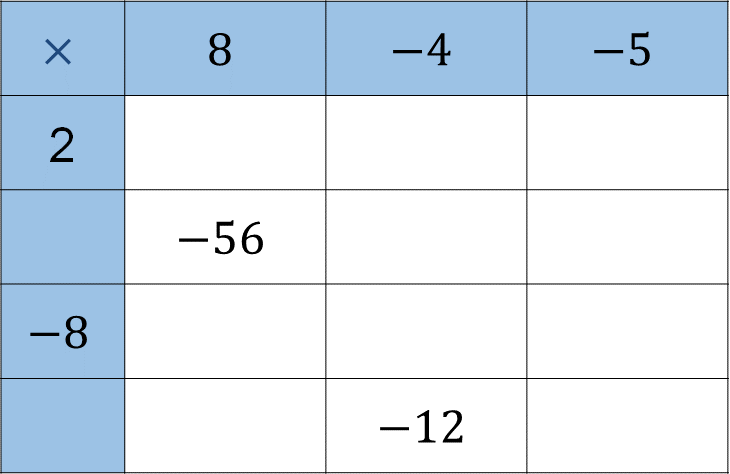
En ella, Yan Carlo, tiene que encontrar tanto los factores, como los productos que faltan.
¿ C ómo se completa la tabla?
Ahora, analiza lo que hizo Yan Carlo:
Él ya sabe cómo llenar el segundo y el cuarto renglón de la tabla, porque simplemente tiene que realizar la multiplicación del número de la columna en azul por el número que se encuentra en el renglón azul.
Entonces, Yan Carlo dice:
-
“ 2 por 8 es 16 ”,
-
“ 2 por -4 es -8 ” y
-
“ 2 por -5 es -10 ”.
Para el cuarto renglón, Yan Carlo dice:
-
“-8 por 8 es igual a -64”,
-
“-8 por -4 es 32” y
-
“-8 por -5 es 40”.
Por lo tanto, el cuadro queda de la siguiente manera:
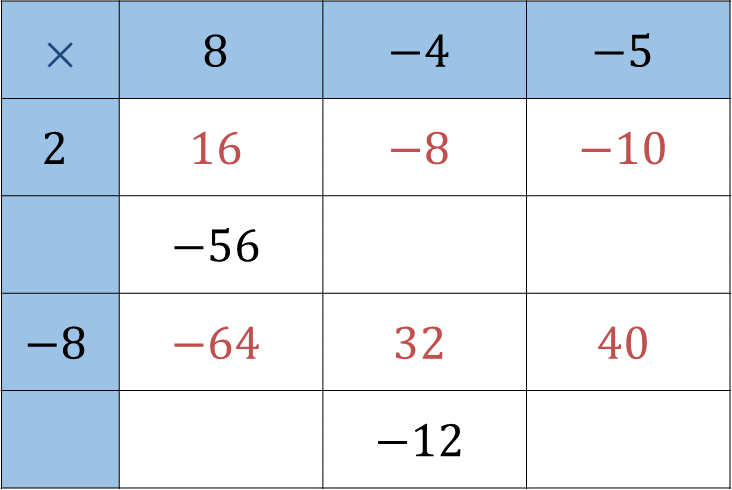
Una vez llenados ambos renglones, retoma “ las reglas para multiplicar los números enteros ”, con el fin de verificar los resultados:
-
“El producto de dos números positivos es positivo”.
-
“El producto de dos números negativos es positivo”.
-
Y, “el producto de un número negativo por un positivo es negativo; o de un número positivo por un negativo también es negativo”.
Ahora, ayuda a Yan Carlo a completar toda la tabla.
¿Cómo le ayudarías a Yan Carlo?
Para lograrlo, reflexiona en lo siguiente:
Se multiplicó (8) por (-8) y el resultado fue (-64).
Qué pasaría si no conocieras el primer factor, pero sí el segundo que es (-8) y conoces también el producto que es (-64), ¿cómo encontrarías el número desconocido?
Necesitas busc ar un número que multiplicado por (-8) dé como resultado (-64):
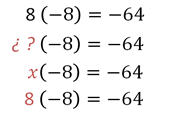
Por lo tanto, el número que se requiere es 8 .
Ahora, observa cómo Yan Carlo llenó el tercer renglón de la tabla.
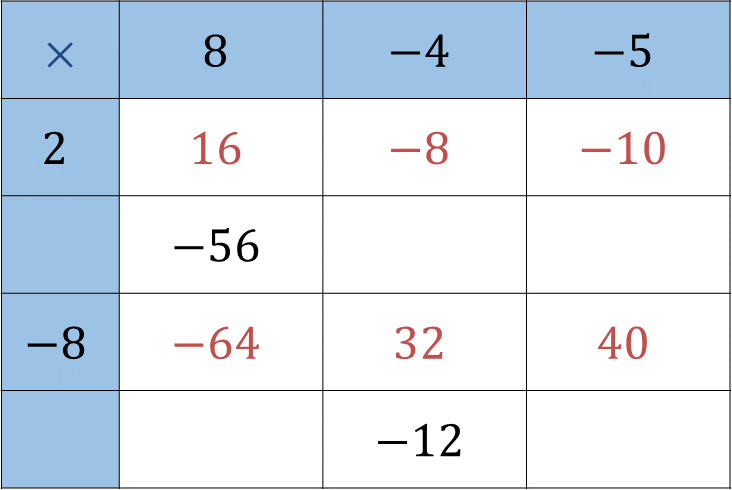
El número que multiplica a 8 y da como producto - 56 es : -7 . Ya que se c onoc e el primer factor que es “-7” , sólo se tiene que multiplicar - 7 por -4 , que es 28 y -7 por -5 , que es 35.
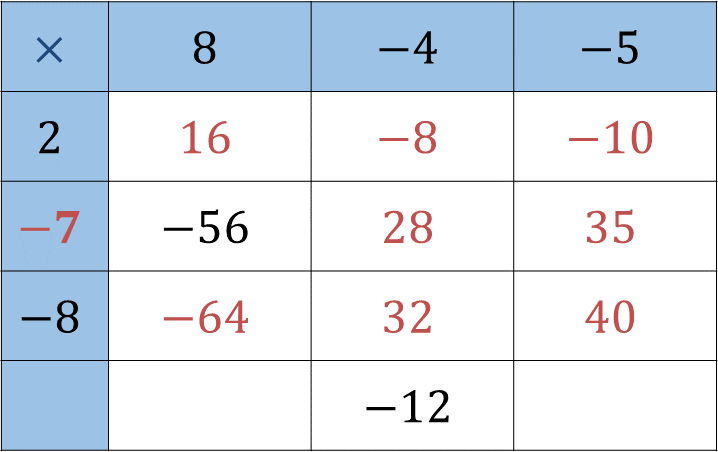
Una vez que Yan Carlo llenó el tercer renglón, procedió a llenar el quinto renglón . Para ello:
Primero buscó un número que multiplicado por -4 dé como resultado -12 , ese número es 3. Entonces “ 3 ” es el factor que coloc ó en la columna azul y en el quinto renglón. Multiplico 3 por 8 igual a 24, y 3 por -5 es igual a -15 .
La tabla completa queda de la siguiente manera:
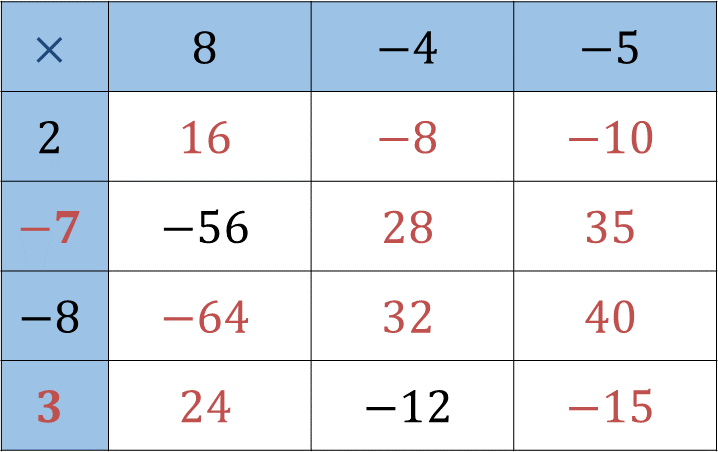
¿Pudiste seguir el procedimiento de Yan Carlo?
U na vez que se completó la tabla, Valeria le da un nuevo reto a su hermano, y le pregunta lo siguiente : ¿ c ómo encontrarías el valor desconocido de “x” en la siguiente operación?
¿Qué número multiplicado por -235 es igual a 42,535?
Yan Carlo responde que ya no es tan fácil encontrar ese número, y que ahora tendrá que aplicar otra estrategia.
Ahora, ayud a a Yan Carlo a responder la pregunta de Valeria. Pero, antes de resolver el ejercicio, toma en cuenta varios puntos.
Primero , partirás de las multiplicaciones de números enteros que ya sabes resolver. Por ejemplo, de la tabla, ya sabes que 3 por 8 es igual a 24. De esta operación , puedes también obtener las siguientes dos expresiones:
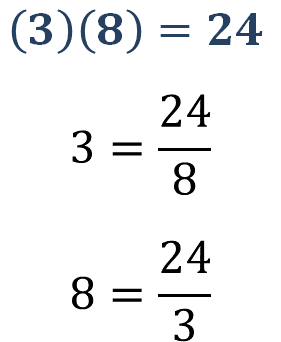
Obsérv a las detenidamente y reflexiona :
¿Por qué 3 es igual a 24 entre 8?
Porque 3 por 8 es igual a 24.
¿Identificaste qué tipo de operaciones estás planteando y resolviendo?
S on dos divisiones. Y las divisiones, como las multiplicaciones, tienen reglas. Así que ya puedes plantear la primera regla para dividir números enteros.
“ Un número positivo entre otro positivo tiene como resultado un número positivo ” .
Usar á s este argumento a lo largo de la sesión, así que recuérd a lo bien, reflexión a lo y sig ue poniendo atención.
Ahora , utili za ese mismo razonamiento para comprender el siguiente ejemplo .
Cuando se completó la tabla, ya sabías que 3 por - 5 es igual a - 15.
Expresando de diferentes formas esta operación, se puede decir que:
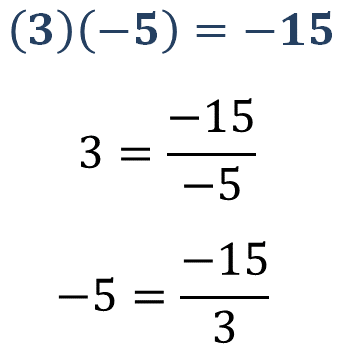
Anali za estas dos últimas expresiones . Como ya tienes los resultados de estas divisiones, ahora vas a reflexionar en su resolución.
¿Cómo se resuelve una división de números enteros?
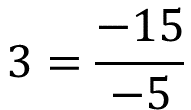
Entonces se dividen los números, y ya sabes que el resultado será un número positivo.
Por lo tanto, la segunda regla para dividir números enteros es:
“Un número negativo entre otro negativo es un número positivo”.
En este caso , también se utilizar á un argumento multiplicativo para explicar la división. Presta atención .
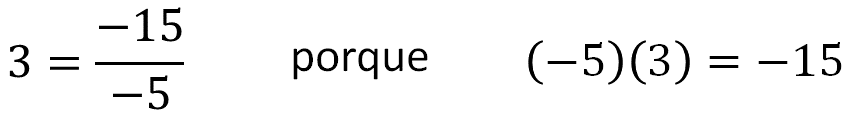
Ahora contin úa con la segunda operación:
¿Cómo se divide 15 negativo entre 3?
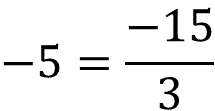
Al dividi r los números , el resultado es un número negativo. También se puede usar el siguiente argumento: la tercera parte de 15 negativo es 5 negativo.
Por lo tanto, la tercera regla para dividir números enteros es:
“Un número negativo entre uno positivo es igual a un número negativo”.
Ahora , el argumento multiplicativo para explicar cómo se hace esta división es el siguiente :
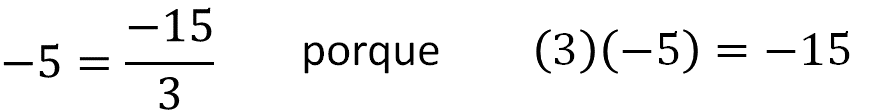
Ya obtuviste la conclusión de que un número negativo entre otro positivo da como resultado un número negativo, pero ¿ q ué pasará con la división de un número positivo entre otro negativo?
Para dar respuesta, analiza la siguiente operación:
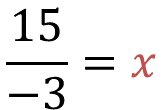
¿Qué número es “x” ?
Como ya lo habías planteado, se resuelve la división, es decir 15 entre 3 igual a 5, pero este sólo es el valor absoluto.
¿Cómo es el resultado, positivo o negativo?
Para saberlo, recurr e al argumento multiplicativo que se ha utilizado:
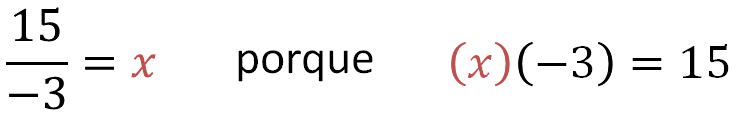
¿Cuál es el valor de “x”?
Ese valor de “x” es 5 negativo, porque 5 negativo por 3 negativo es igual a 15.
Así que resolvis te la división de 15 entre 3 negativo y el resultado es 5 negativo.
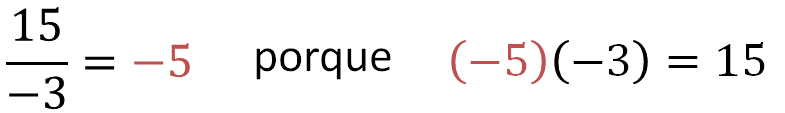
Entonces, la siguiente regla es que :
“Un número positivo entre un número negativo es negativo”.
Ahora ya puedes responder la pregunta que le hizo Valeria a su hermano Yan Carlo :
¿Qué número multiplicado por 235 negativo es igual a 42,535?
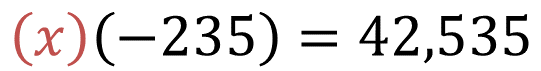
¿Cómo se encuentra ese número “x” ?
Puedes transformar la multiplicación en una división, porque la multiplicación y la división son operaciones inversas.
Aquí es donde Yan Carlo se da cuenta de que para encontrar el valor de “x”, la estrategia que debe aplicar es: utilizar una expresión equivalente a la multiplicación, la de una división y resolverla.
La división a resolver es la siguiente:
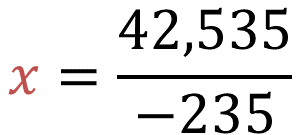
El resultado será negativo, porque un número positivo entre otro negativo es negativo.
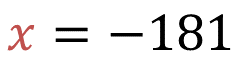
Por lo tanto, e l número que buscaba Yan Carlo es 181 negativo.
Toma en cuenta que se encontró el factor desconocido mediante una división. Por ello , se dice que la multiplicación y la división son operaciones inversas.
Entonces, ahora que ya sabes cómo dividir números enteros, practi ca la división de estos números. Para ello, retom a a Yan Carlo y Valeria.
Situación, tabla de dividir
Ahora, la maestra de Yan Carlo le dejó la siguiente tarea:
Tiene que llenar esta tabla de dividir, considerando que en el renglón azul se tiene al dividendo y en la columna azul, al divisor.
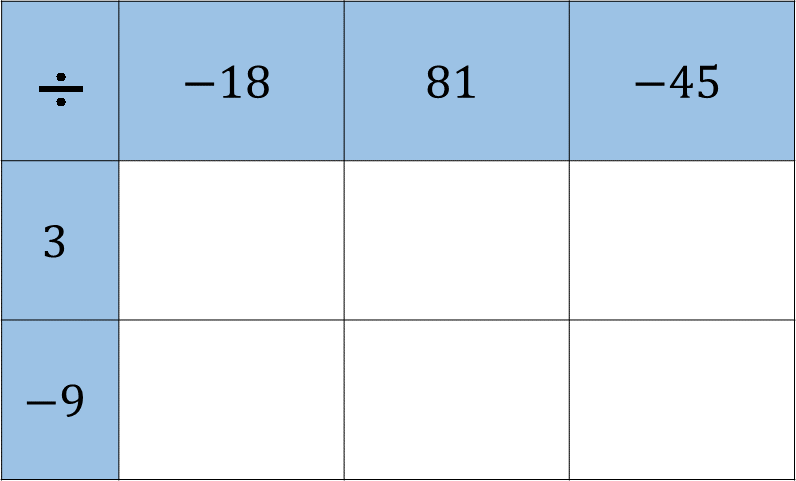
R ealiza las operaciones de división de enteros y completa la tabla.
Observa cómo lo hizo Yan Carlo. C om enzó con el segundo renglón:
-
-1 8 entre 3 es igual a - 6, porque 18 entre 3 es 6, y un número negativo entre uno positivo resulta en uno negativo. Además, también se puede calcular sabiendo que la tercera parte de 18 negativo es 6 negativo.
-
Después , 81 entre 3 es 27 . E sta es una división normal, es decir , entre dos números positivos, cuyo resultado es positivo.
-
Finalmente , - 45 entre 3 es igual a - 15, porque 45 entre 3 es 15 y un número negativo entre uno positivo tiene como resultado un número negativo. También la tercera parte de - 45 es - 15.
Por lo tanto, la primera parte de la tabla, quedo de la siguiente manera:
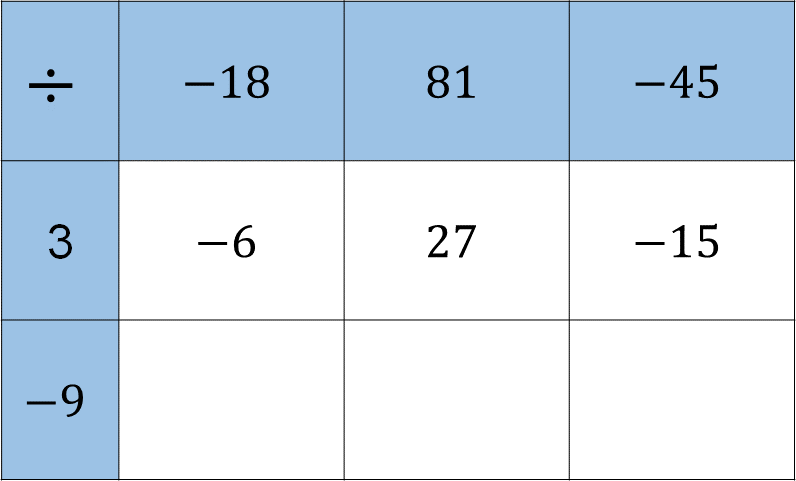
¿Qué te parecieron las estrategias de Yan Carlo para dividir números enteros?
Analiza ahora otra estrategia que utilizó para llenar el tercer renglón, cuando su hermana Valeria le propuso:
“Ahora, te reto a que utilices el argumento multiplicativo para resolver el segundo renglón”.
Observa cómo lo hizo:
-
En el tercer renglón se tiene la división, -18 entre -9, que es igual a 2. Porque 2 por 9 negativo es igual a 18 negativo.
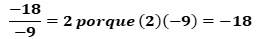
-
Después, dividió 81 entre -9 y el resultado es igual a -9. Porque 9 negativo por 9 negativo es igual a 81.
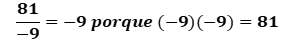
-
Para la última división, -45 entre -9 es igual a 5. Porque 5 por 9 negativo es igual a 45 negativo.
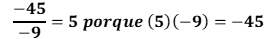
Al finalizar, la tabla quedo de la siguiente manera:
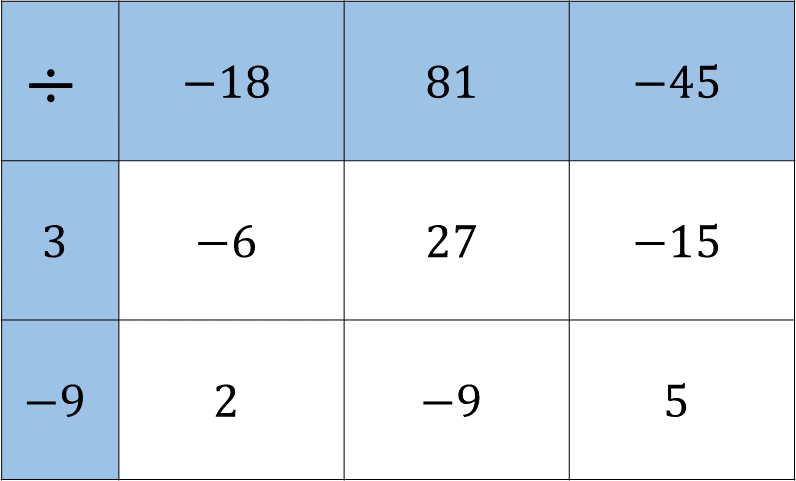
Con esto, se utiliza ron diferentes estrategias para dividir números enteros.
Has realizado varias divisiones de números enteros, y se presentaron en forma de fracción. Pero también se pueden escribir de otras formas; por ejemplo, las siguientes expresiones corresponden a la misma operación de división:

En la primera columna, las divisiones aparecen indicadas en forma de fracción, en la segunda columna aparecen las mismas divisiones en forma horizontal, y en la tercera columna aparecen las divisiones indicadas con una diagonal. Son tres formas que indican la misma operación.
Ahora que ya sabes resolver divisiones de números enteros, realiza la siguiente actividad.
Trata de resolver las 4 divisiones de números enteros que se mostraron en la tabla anterior, aunque estén escritas de diferente forma.
Cuando hayas terminado la actividad anterior, comprueba tus resultados con la siguiente información. Si no obtuviste los resultados correctos , no t e preocupe s , tóm ate t u tiempo y verifi ca con calma t us resultados, lo importante es que aprenda s cómo se resuelven estas operaciones y qué información necesitas para hacerlo.

Hasta ahora, has hecho divisiones con números enteros, positivos y negativos. Pero ¿ q ué pasa con el cero?
El cero también es un número entero y , como sabe s, no es positivo ni negativo. El cero también puede intervenir en una división de números enteros:
Observa los siguientes casos:
-
Cero entre un número positivo o negativo.
-
Cero entre cero.
-
Un número positivo o negativo entre cero.
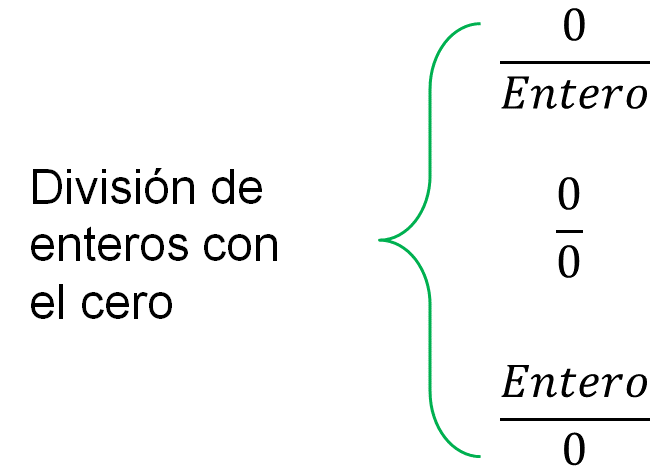
Cuando se divid e cero entre cualquier número entero, ya sea positivo o negativo, el resultado es cero. Por ejemplo: c ero entre 5 es igual a 0 porque, utilizando el argumento multiplicativo, cero por cinco es igual a cero.
Asimismo, cero entre 5 negativo es igual a cero, porque cero por 5 negativo es igual a cero.
¿Qué pasa en los otros dos casos?
Reflexion a:
¿Has pensado en alguna situación en la que tengan que dividir entre cero?
Parecería no tener sentido. Para concluir, reali za en t u calculadora una división entre cero, por ejemplo, 5 entre cero, 5 negativo entre cero o cero entre cero y observa el resultado que te arroja.
Has finalizado la sesión, dedicada a dar sentido y significado a la división de números enteros. S i te quedaron dudas, puede s repasar los argumentos que se utiliza ron para realizar una división de números enteros.
Recuerd a que este es un material de apoyo, y para complementar lo estudiado puede s consultar otras fuentes, como t u Libro de Texto de Matemáticas de segundo grado.
El r eto de h oy:
¿Cómo resolvería s la siguiente división?
A (-210) divídelo entre (-2), el resultado divídelo entre ( 3 ) , después vuélvelo a dividir entre (- 5 ) y el último resultado entre ( 7 ) .
¿Cuál fue el cociente final?
Describ e el procedimiento para resolver una división sucesiva con números enteros, y menciona cómo sabría s si el resultado será un número positivo o negativo.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas


Login to join the discussion