Desarrollos planos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:05Aprendizaje esperado: Calcula el volumen de prismas y cilindros.
Énfasis: Construir el desarrollo plano de prismas rectos cuya base sea un polígono regular.
¿Qué vamos a aprender?
Continuarás con el estudio del volumen de prismas y cilindros rectos. En esta sesión, conocerás cómo construir el desarrollo plano de estos cuerpos geométricos cuya base sea un polígono regular, a través de diversas situaciones.
¿Qué hacemos?
Reflexiona sobre las siguientes preguntas, anótalas y ve contestándolas durante esta sesión:
- ¿Por qué es importante conocer el desarrollo plano de los cuerpos geométricos?
- ¿Qué características tienen los desarrollos planos?
- ¿Cómo es que del desarrollo plano se pasa a la construcción del cuerpo geométrico?
- ¿Cómo se construye el desarrollo plano de un cuerpo geométrico específico?
Analiza el primer planteamiento.
Situación-problema. La nueva caja triangular
Lía tiene un restaurante y adquiere cajas de base triangular que utiliza para vender comida para llevar o servir porciones de pizza, de tarta u otros alimentos. La base y tapa de estas cajas son triangulares.
Las dimensiones de una nueva caja con base triangular son las siguientes:
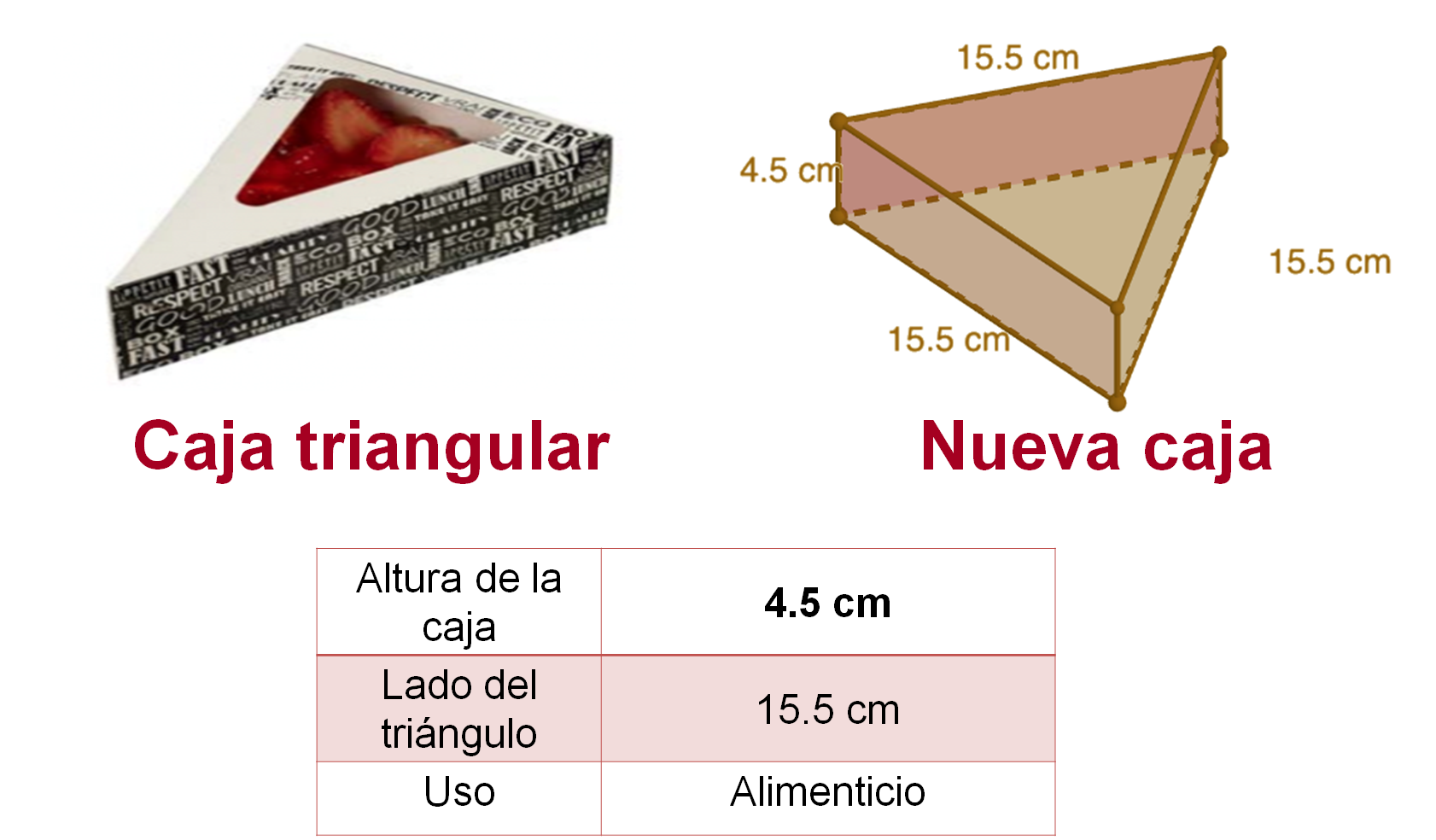
Lía quiere elaborar las nuevas cajas con papel reciclado o biodegradable. Con este fin, desarmó una caja para usarla como plantilla y poder crear nuevos diseños.
Una vez desarmada la caja, le llamó a Caleb, que es el diseñador de la tienda, para describirle la plantilla.
¿Cómo describirías las características de la caja desarmada?
Analiza la caja triangular y registra qué características identificas en la caja, qué figuras reconoces y describe cómo piensas que sería la plantilla, o como se dice en matemáticas, su desarrollo plano.
Sobre el planteamiento de Lía, el uso de cajas en la industria alimenticia es grande, y elaborarlas con papel reciclado o biodegradable es una buena alternativa para el cuidado del planeta.
El desarrollo plano se podría describir de la siguiente manera:
Tiene dos caras de forma triangular, ambas caras son congruentes o iguales; además, tiene tres caras de forma rectangular que también son iguales.
La base de la caja es un triángulo equilátero que mide 15.5 cm de lado.
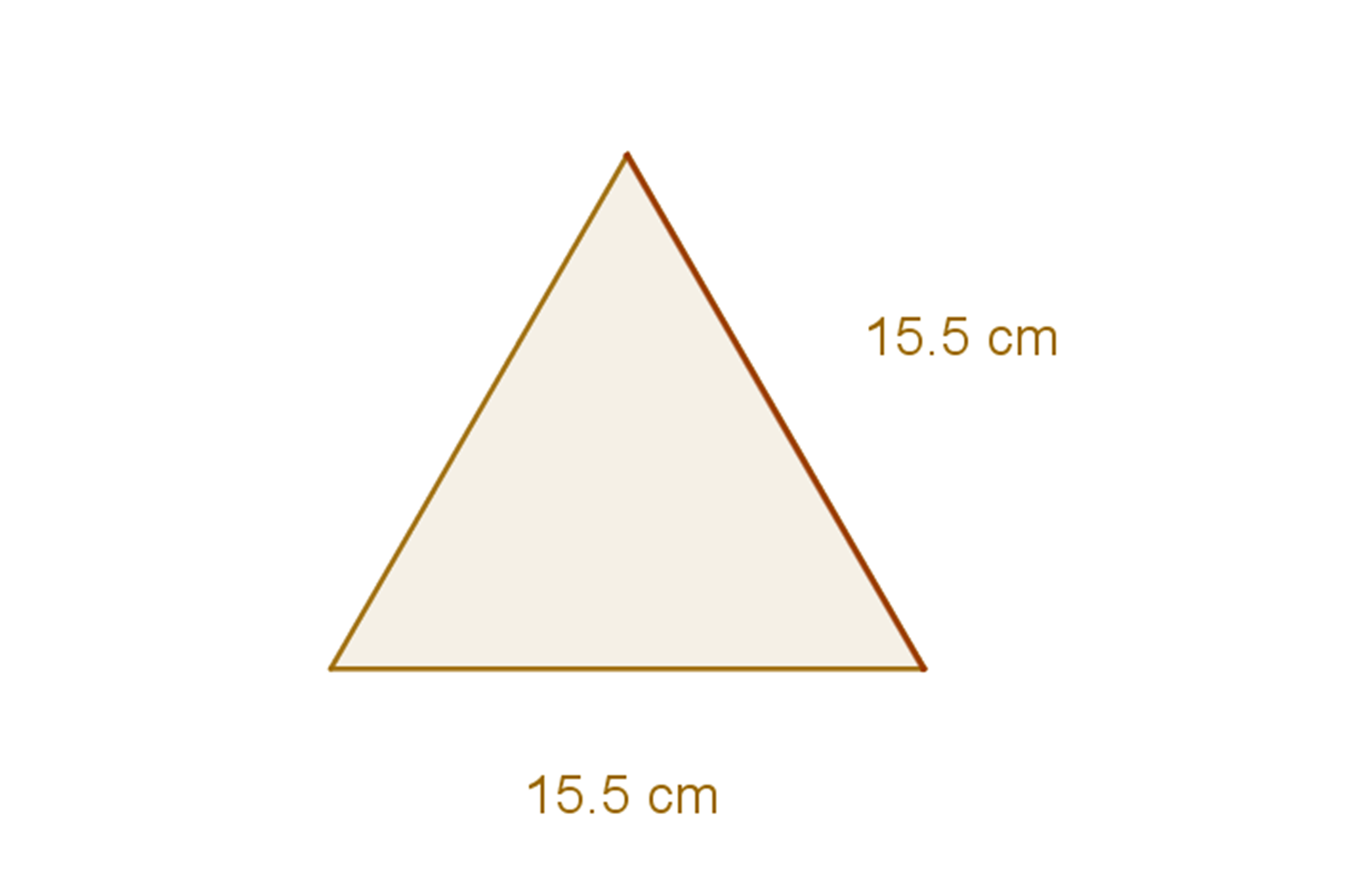
Sus caras laterales rectangulares son iguales. En cada una de las tres caras rectangulares, dos de sus lados miden 4.5 cm para que la caja mantenga la misma altura. Además, las caras laterales son rectángulos congruentes, cuyo largo es de 15.5 cm.
Lía le describió a Caleb la plantilla y él le envío el siguiente modelo. Analízalo:
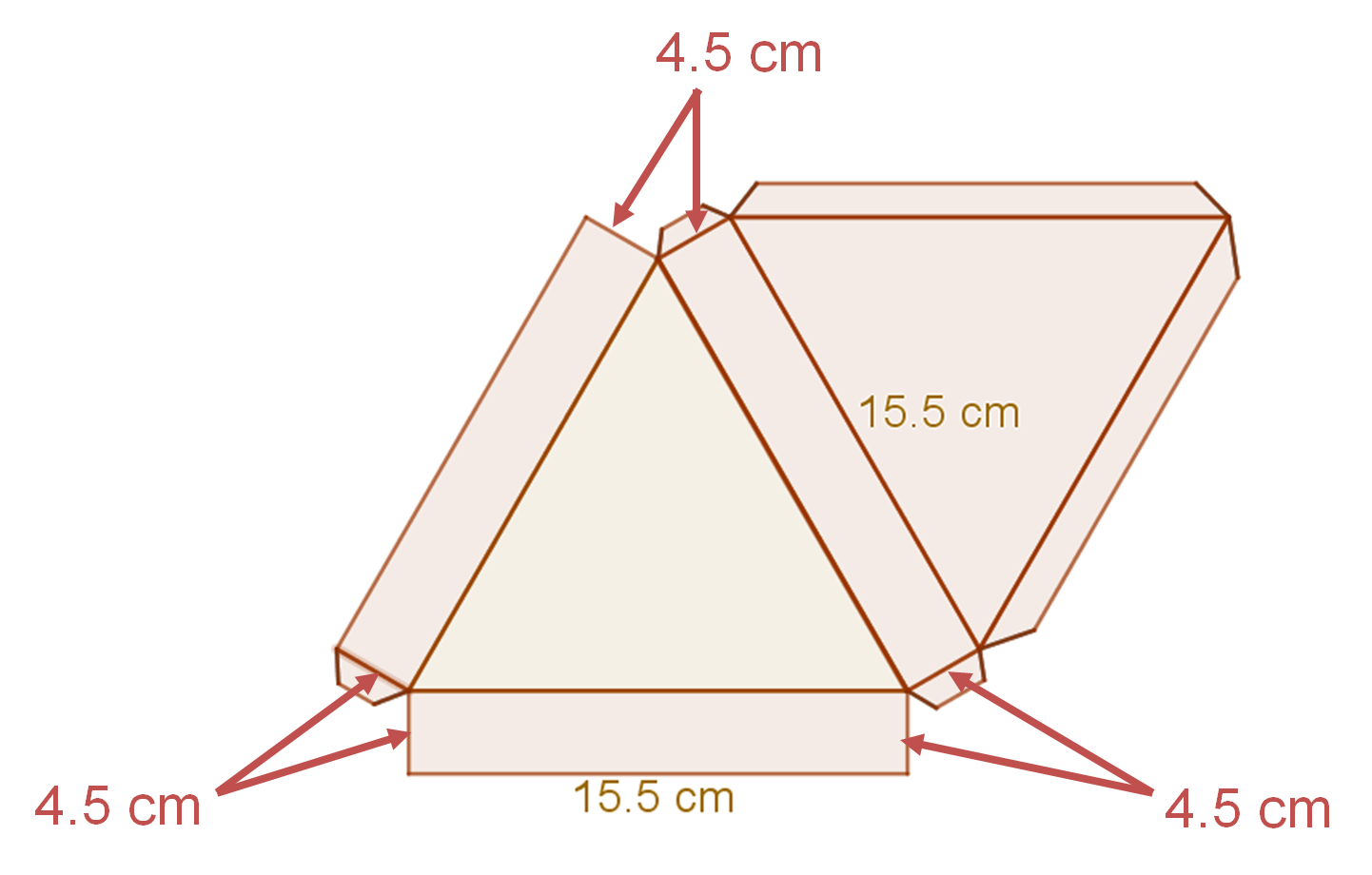
El desarrollo plano que elaboró Caleb tiene dos caras triangulares iguales o congruentes; tres caras rectangulares, cuyas alturas son las mismas, y también las medidas de su largo son congruentes.
Reflexiona en lo siguiente:
La caja anterior, ¿es un poliedro?
En matemáticas un poliedro es un cuerpo geométrico tridimensional cuyas caras son polígonos. Existen diferentes tipos de poliedros: a los que tienen dos caras iguales, conocidas como bases, y caras laterales rectangulares, se les denomina prismas.
Observa los siguientes prismas de base triangular:
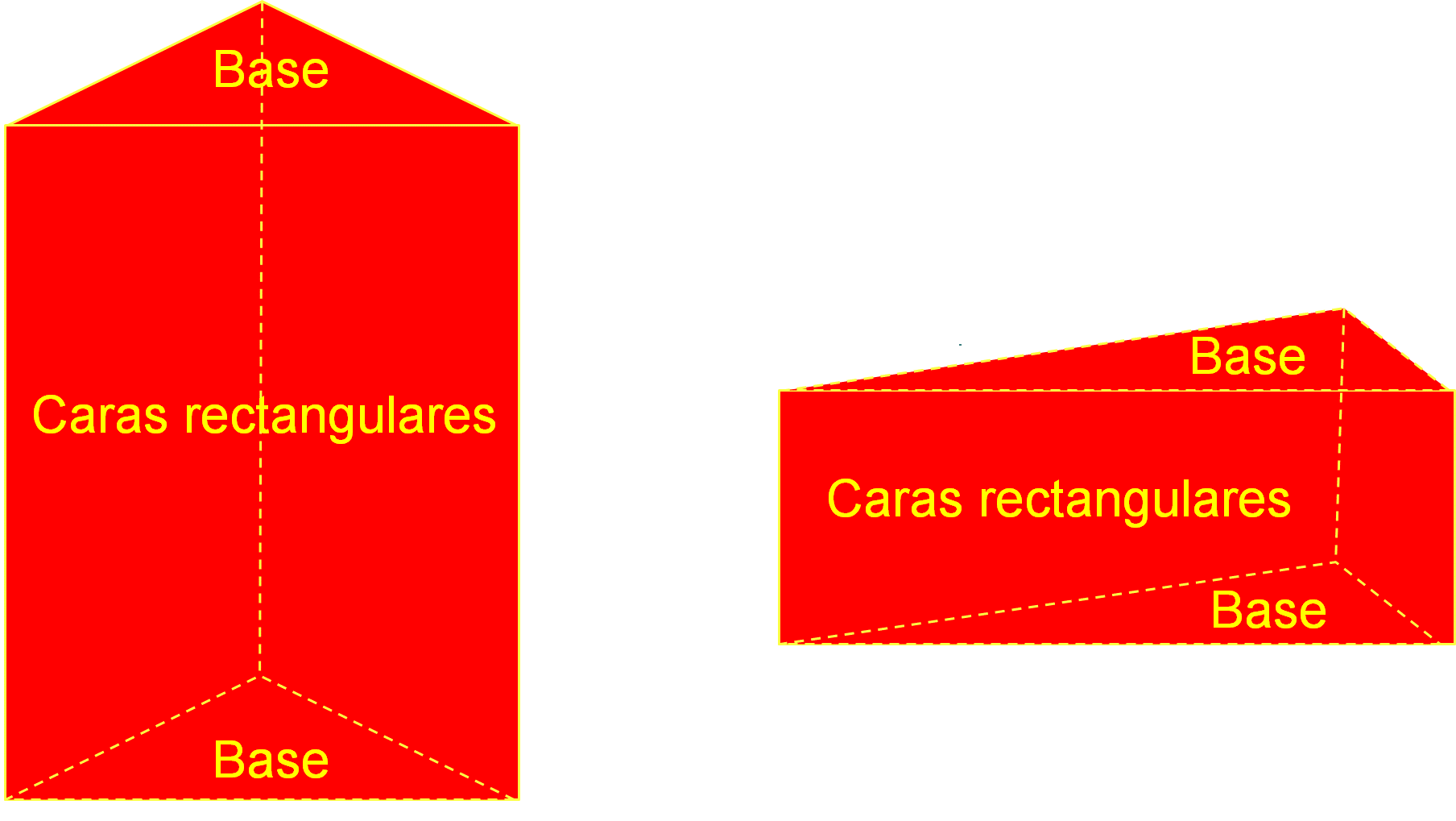
- El primero, es un prisma recto de base triangular, sus bases tienen forma de triángulos equiláteros.
- El segundo, es un prisma recto de base triangular, sus bases tienen forma de triángulos rectángulos isósceles.
Ahora, analiza la siguiente información:
Desarrollos Planos
Todos los prismas son desarrollables, es decir, sus caras pueden ubicarse en un plano y mediante pliegues se puede construir el prisma.
El desarrollo plano de un prisma recto está compuesto por sus dos bases y por un rectángulo que tiene tantas divisiones como número de caras laterales.
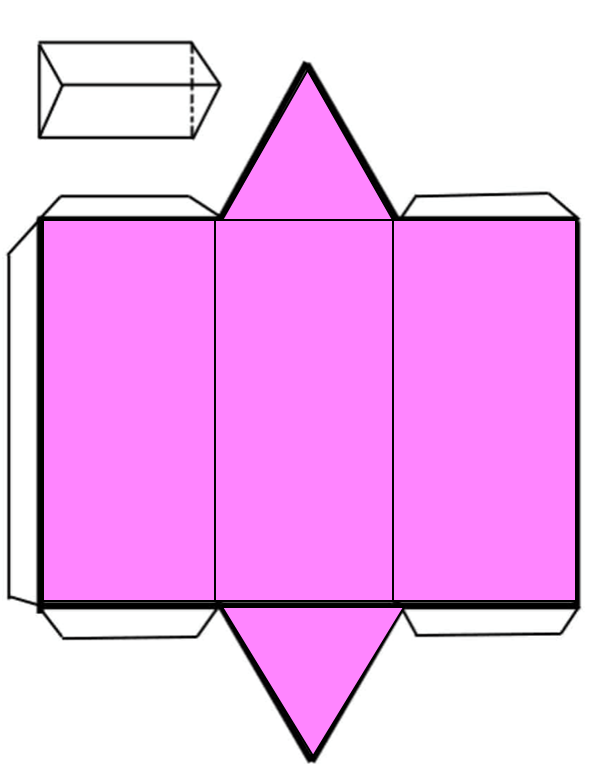
En la figura anterior, se puede observar un prisma recto de base triangular, y su desarrollo plano está conformado por dos triángulos que forman sus bases y 3 rectángulos que forman sus caras laterales.
Ahora reflexiona sobre las siguientes preguntas:
¿Sólo hay un desarrollo plano para construir un prisma?
¿Es posible hacer un análisis geométrico para determinar el desarrollo plano o los desarrollos planos de un mismo prisma?
Para dar respuesta a las preguntas anteriores y enriquecer tus argumentos, observa el siguiente audiovisual, en el que analizarás la situación de Carolina.
- Moldes para cajas. 25 seg.
https://www.youtube.com/watch?v=cwdwFY-cWsI
En el audiovisual anterior, se mencionó que el cubo tiene 11 desarrollos planos, aunque sólo se analizaron cuatro. Los desarrollos planos con los que no se arma un cubo presentaron dos características:
- Sus caras se empalman o se superponen.
- Al armar el cubo, quedan huecos o faltan caras para completarlo.
Estas características serán de utilidad para construir el desarrollo plano o los desarrollos planos de un mismo prisma, o de diferentes prismas.
Ahora, ayuda a Carolina a verificar si con el desarrollo plano E se arma la caja que le interesa y contesta las preguntas que plantea Raquel.
Analiza la caja que necesita armar Carolina.
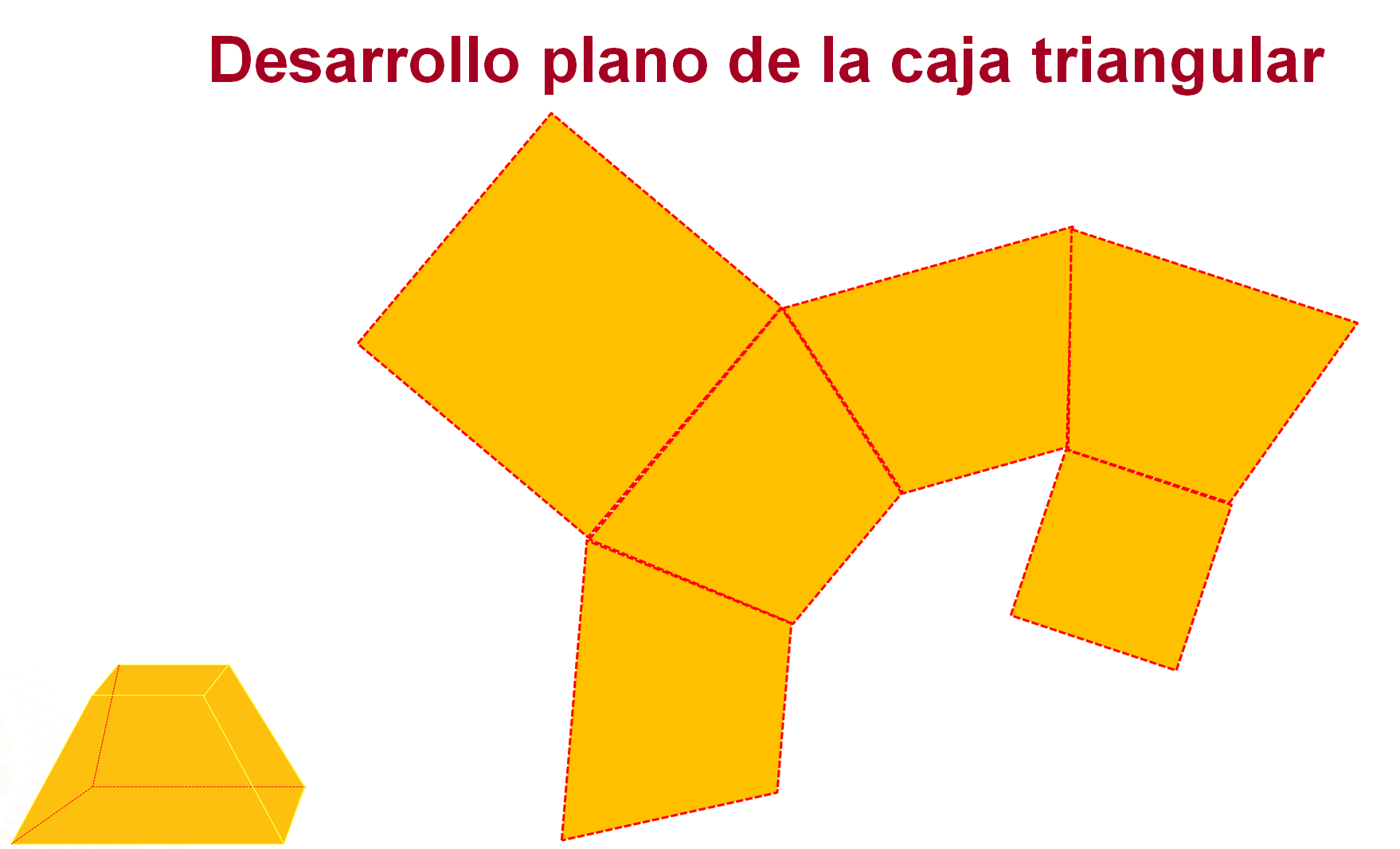
- La caja tiene dos bases de forma cuadrangular. Observa que las bases de las cajas no son congruentes o iguales.
- La caja tiene 4 caras de forma trapezoidal. Dado que la base es cuadrangular, sus 4 caras laterales son congruentes.
Probablemente en tu análisis identificaste otras características de las figuras; anótalas.
Ahora asigna medidas a las figuras para que traces el desarrollo plano. Empieza trazando una de sus bases, donde los lados miden lo mismo, ya que tienen forma de cuadrado. Puedes trazar un cuadrado de 10 cm de lado o las que consideres adecuadas.
En uno de los lados traza un trapecio, la medida de su base mayor es de 10 cm; su altura, de 7 cm, y su base menor mide 5 cm. Ya tienes en el plano dos caras del desarrollo de la caja.
Después, sobre uno de los lados del trapecio se traza otro trapecio congruente. Y luego se trazan dos más para tener 4. Cada trapecio representa una de las caras laterales de la caja.
Finalmente, en la base menor de uno de los trapecios se traza un cuadrado de 7 cm de lado. No puede tener otra medida, pues de lo contrario, no se formaría la caja.
Seguramente te puedes preguntar por qué se trazó el cuadrado sobre la base menor de ese trapecio.
El cuadrado de menor tamaño funge como “tapa de la caja”, por lo que puede trazarse en cualquiera de las bases menores de los trapecios que forman las caras laterales de la caja, como se muestra en la opción 2 o 3.
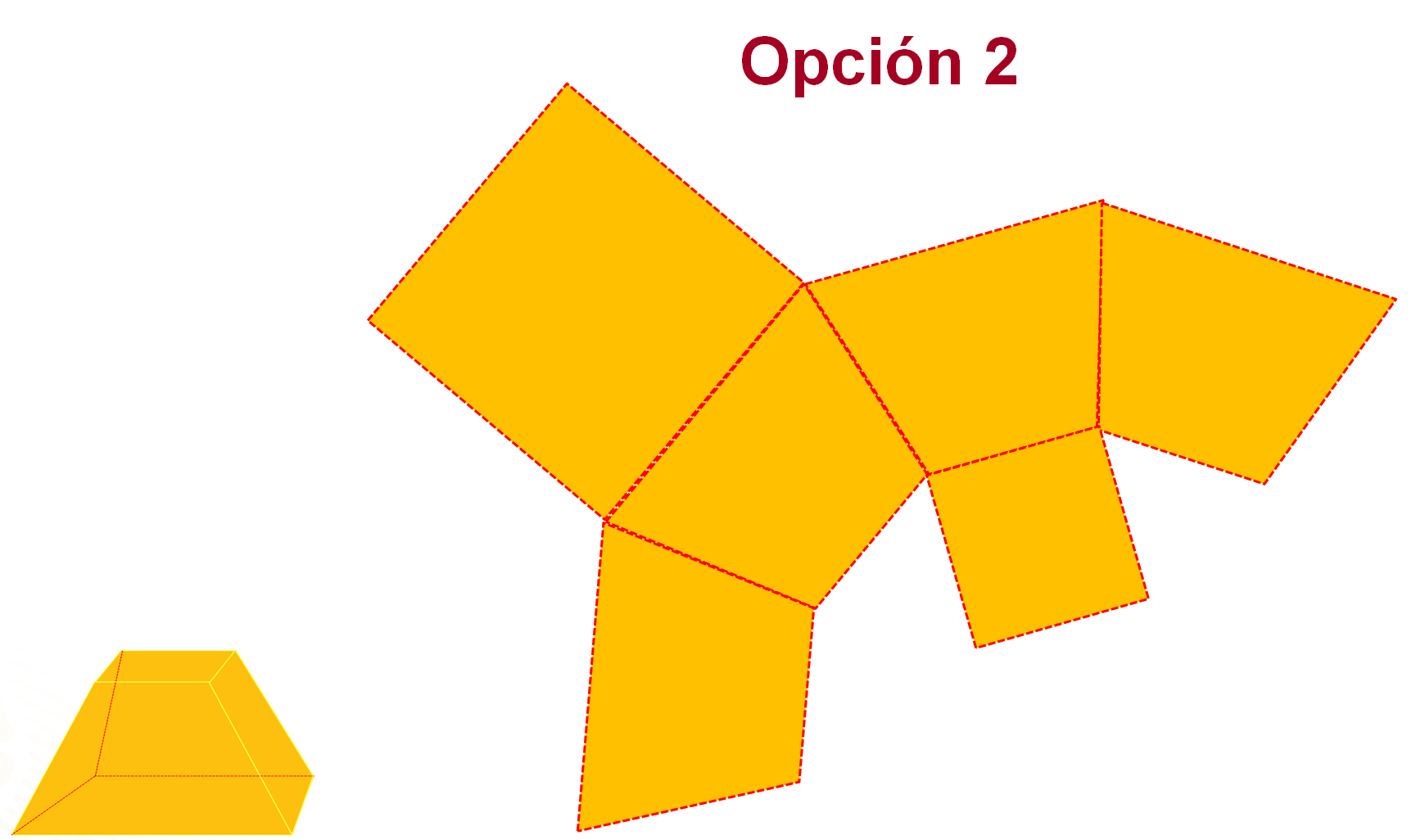
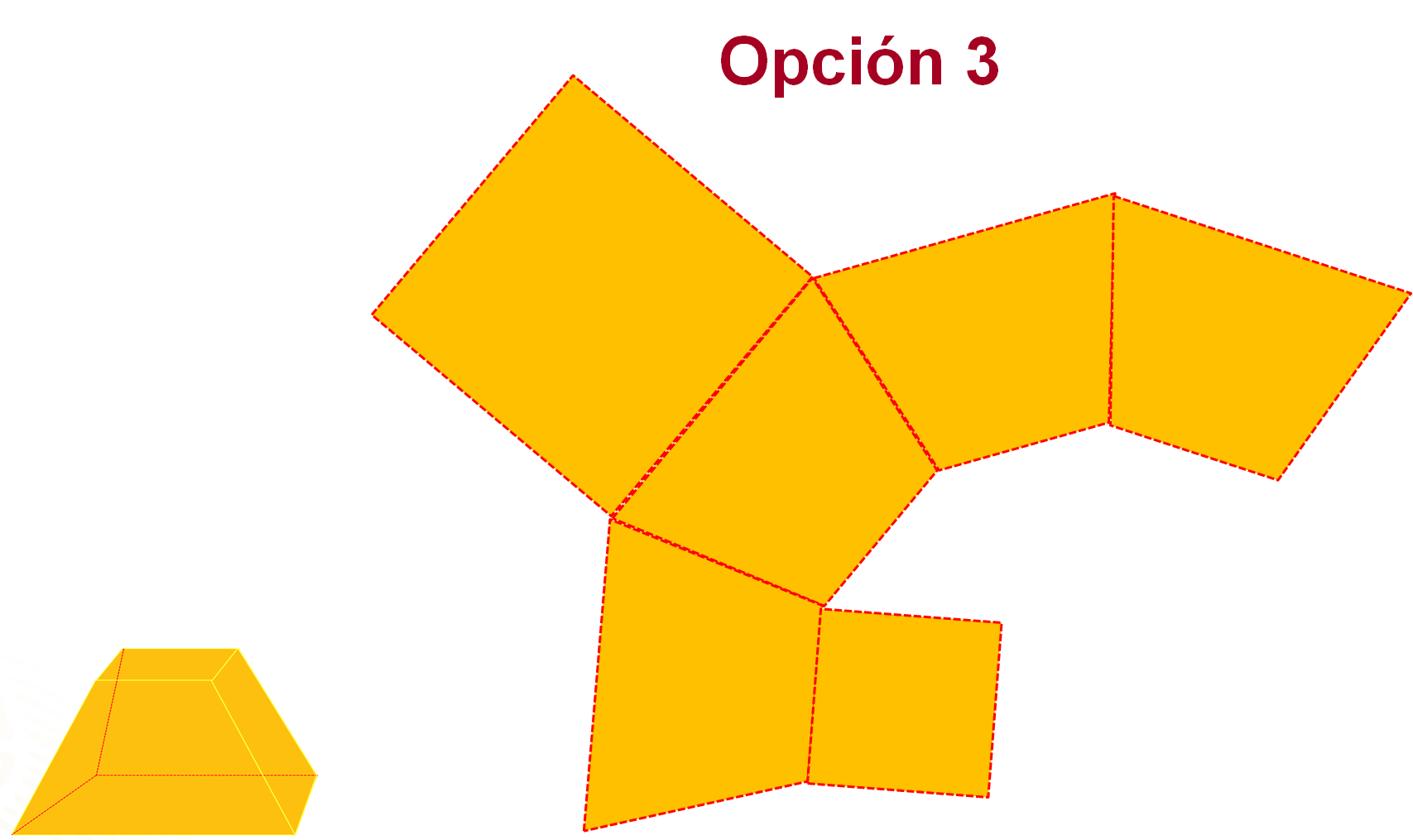
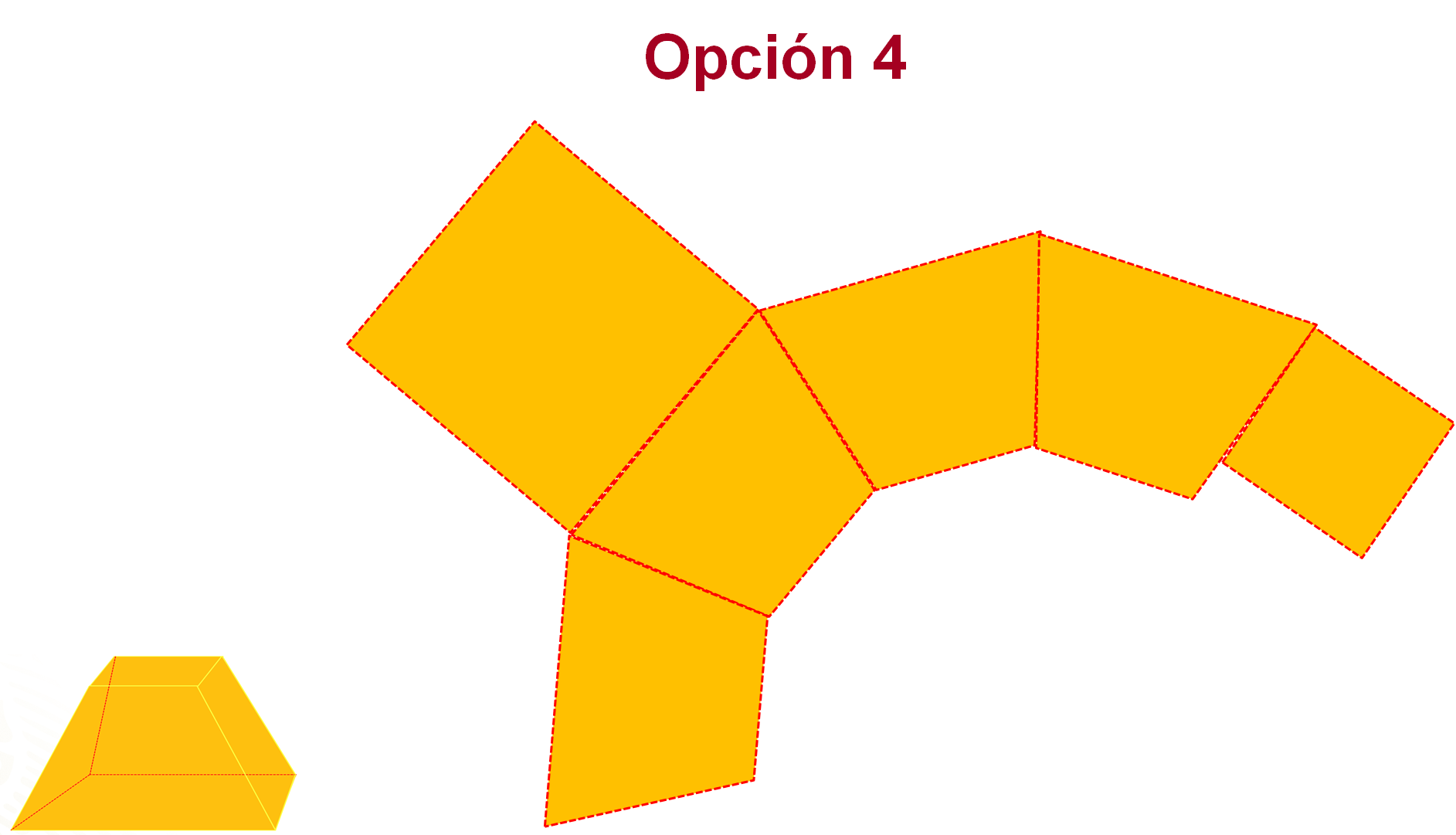
Sin embargo, al trazar el cuadrado de menor tamaño en uno de los lados del trapecio (opción 4), no se podría armar la caja, pues ésta quedaría sin tapa y tendría 5 caras laterales, 4 iguales y una diferente.
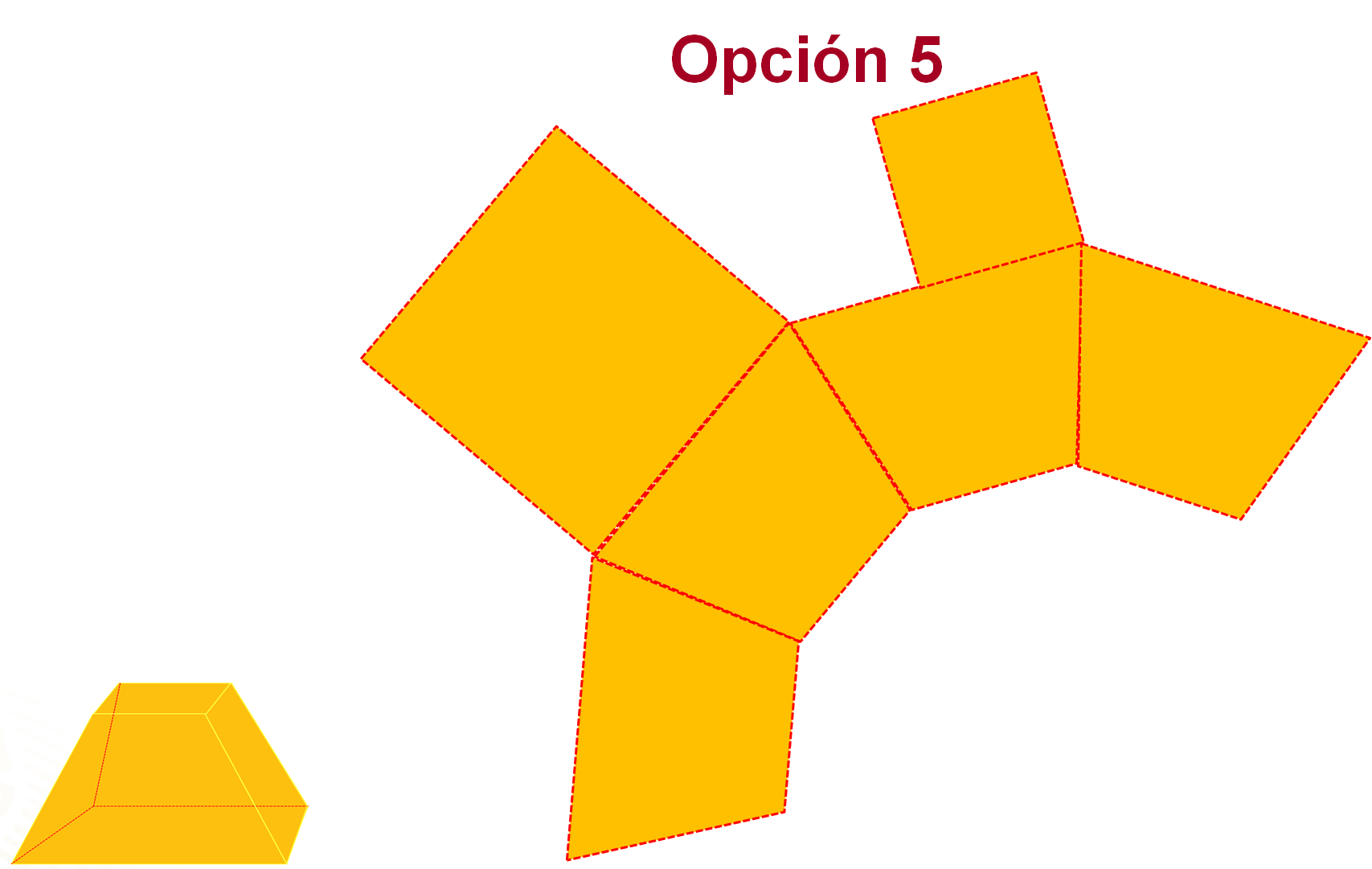
Asimismo, al trazar el cuadrado de menor tamaño en una de las bases mayores de los trapecios (opción 5), no se podría armar la caja, pues ésta quedaría sin tapa y tendría 2 bases de distinto tamaño que se superpondrían o empalmarían.
Analiza lo siguiente:
¿Cómo se puede construir un desarrollo plano si no se tiene una caja para desarmarla?
¿O cómo se puede validar un desarrollo plano si no se tiene un desarrollo plano propuesto?
Para lograrlo, hay que verificar que exista una correspondencia entre el número de bases de la caja o, en su caso, del cuerpo geométrico y su desarrollo plano.
Hasta ahora, has visto el desarrollo plano de prismas rectos donde sus bases son iguales o congruentes, sus caras laterales, en los prismas rectos, son rectangulares y congruentes. También de cuerpos geométricos, donde sus bases, aunque tienen la misma forma, no tienen el mismo tamaño, sus caras laterales no son rectangulares, pero sí son congruentes o iguales. En este caso, la caja es una pirámide cuadrada trunca, que no corresponde a un prisma.
Ahora, profundiza en el estudio de los desarrollos planos de los prismas. Para ello, reflexiona en la siguiente pregunta:
¿Cómo saber cuántas caras laterales se deben de trazar en el desarrollo plano de cualquier prisma recto?
Con lo que has aprendido, realiza la siguiente actividad.
Elabora tus propias definiciones y características de desarrollos planos y considera lo siguiente:
El número de caras laterales de un cuerpo geométrico debe de ser correspondiente a su desarrollo plano. Esta información la provee el número de lados de la forma de sus bases. De esta manera, al armar el desarrollo plano, las caras no se superponen ni se dejan huecos.
Una vez concluida la actividad anterior, estudiarás la relación entre un desarrollo plano y el volumen del cuerpo geométrico que se construye con él.
Analiza el desarrollo plano de un prisma recto de base pentagonal.
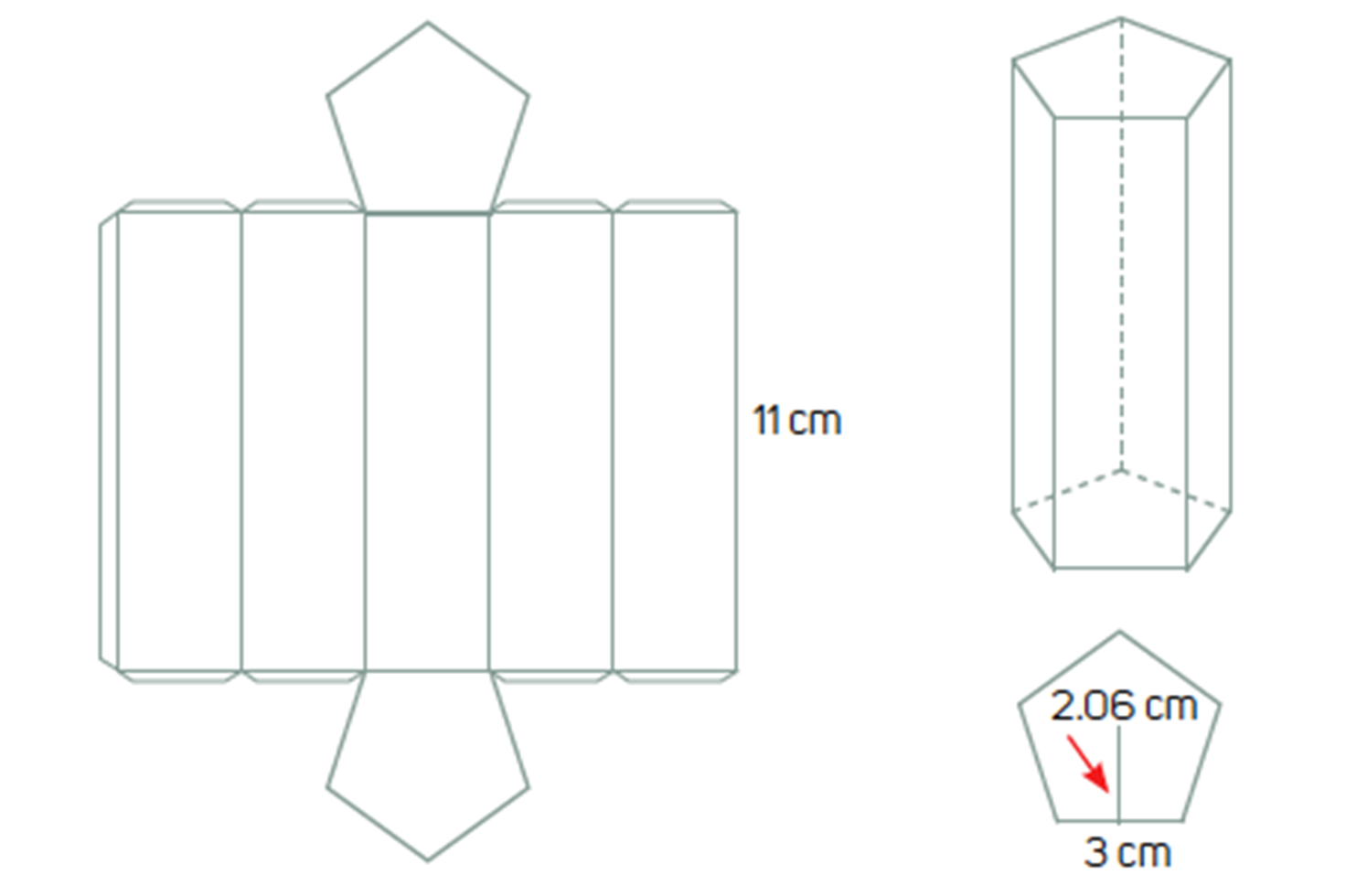
Este prisma tiene dos bases, en este caso, con forma pentagonal, y son iguales. Cada lado del pentágono mide 3 cm y su apotema mide 2.06 cm.
¿Cuánto mide cada cara rectangular?
Mide 3 cm de base y 11 cm de altura.
Para calcular el volumen de un prisma, se emplea la siguiente fórmula:
V = área de la base por h
Por lo tanto, necesitas conocer la medida del área de la base, esto es, el área del pentágono regular es un medio del perímetro, por la medida de la apotema:
A= (5)(3) (2.06) / 2 = 15.45 cm cuadrados
Ahora sustituye los valores:
V= (15.45) (11) = 169.95 cm cúbicos
Al armar el cuerpo geométrico, su volumen es de 169.95 cm cúbicos.
Ahora ¿cuál es el desarrollo plano de un cuerpo geométrico que mide 375 cm cúbicos y de altura 15 cm?
¿Cómo puedes determinarlo?
¿Cuántas opciones tienes?
¿Cómo es la forma de sus bases?
El volumen de un cuerpo geométrico se obtiene al multiplicar la medida de la altura por el área de la base.
En este caso, el volumen es de 375 centímetros cúbicos y tiene 15 cm de altura; necesitas encontrar la medida del área de la base. Para ello divide 375 entre 15, cuyo cociente es 25. Como lo que buscas es la medida de la base, ésta mide 25 cm cuadrados. ¿Cuál puede ser la forma de la base del prisma?
Para ello, tienes un número infinito de posibilidades, pues puedes trazar todas aquellas figuras cuya medida de área sea igual a 25 cm cuadrados.
Observa el siguiente cuadro, donde conocerás algunas figuras, cuya medida de área sea igual a 25 cm cuadrados

Esto se verifica al obtener el volumen: multiplica el área de la base por 15 cm de altura y obtendrás en todos los casos 375 cm cúbicos de volumen.
Observa las siguientes dos opciones de desarrollos planos que corresponden a dos cuerpos geométricos, cuyo volumen es de 375 cm cúbicos. Se trata de un prisma recto de base cuadrangular y un prisma de base rectangular.
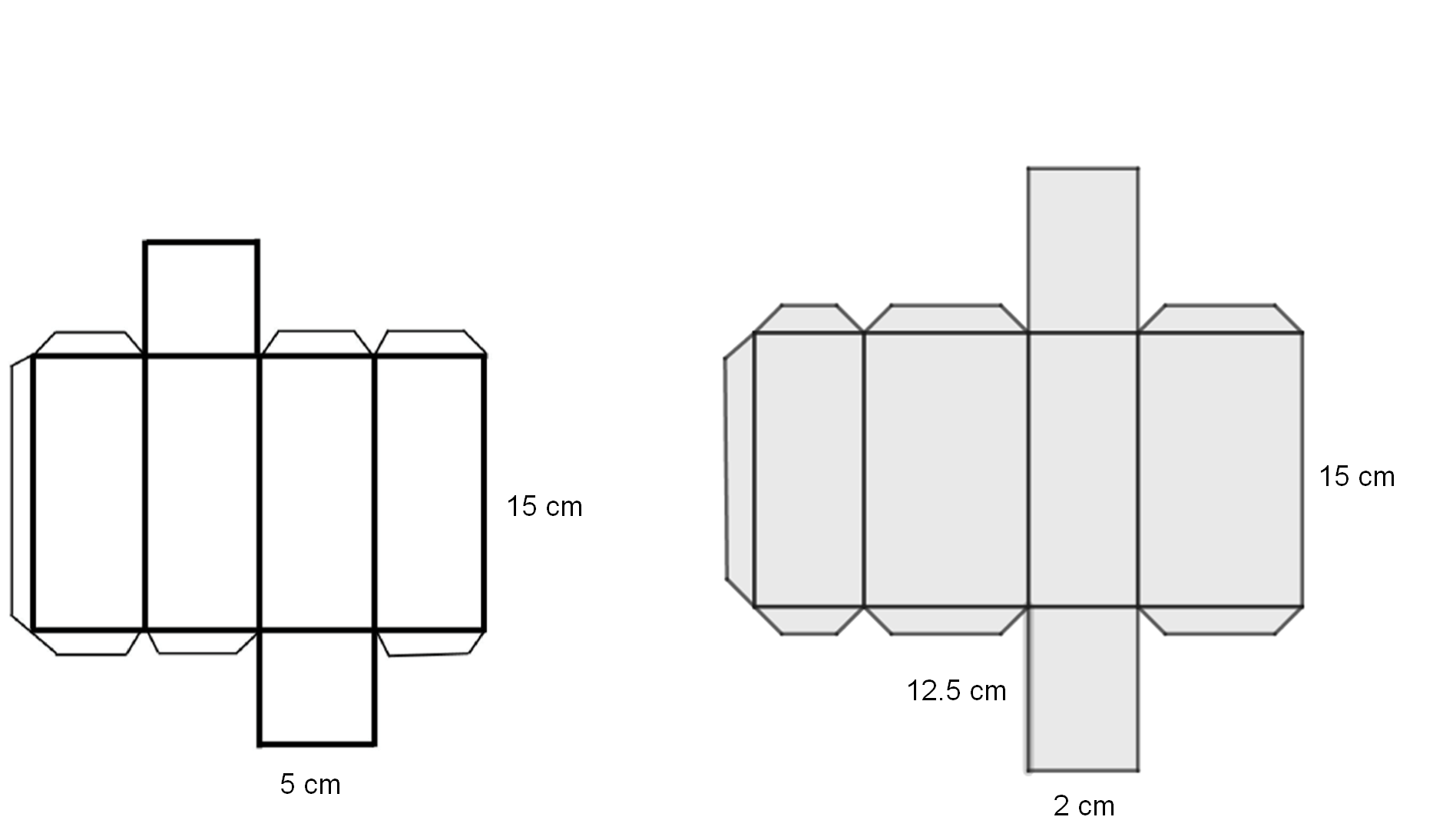
Las siguientes opciones muestran dos desarrollos planos. El primero de ellos tiene las bases de forma triangular; la segunda opción tiene bases de forma pentagonal.
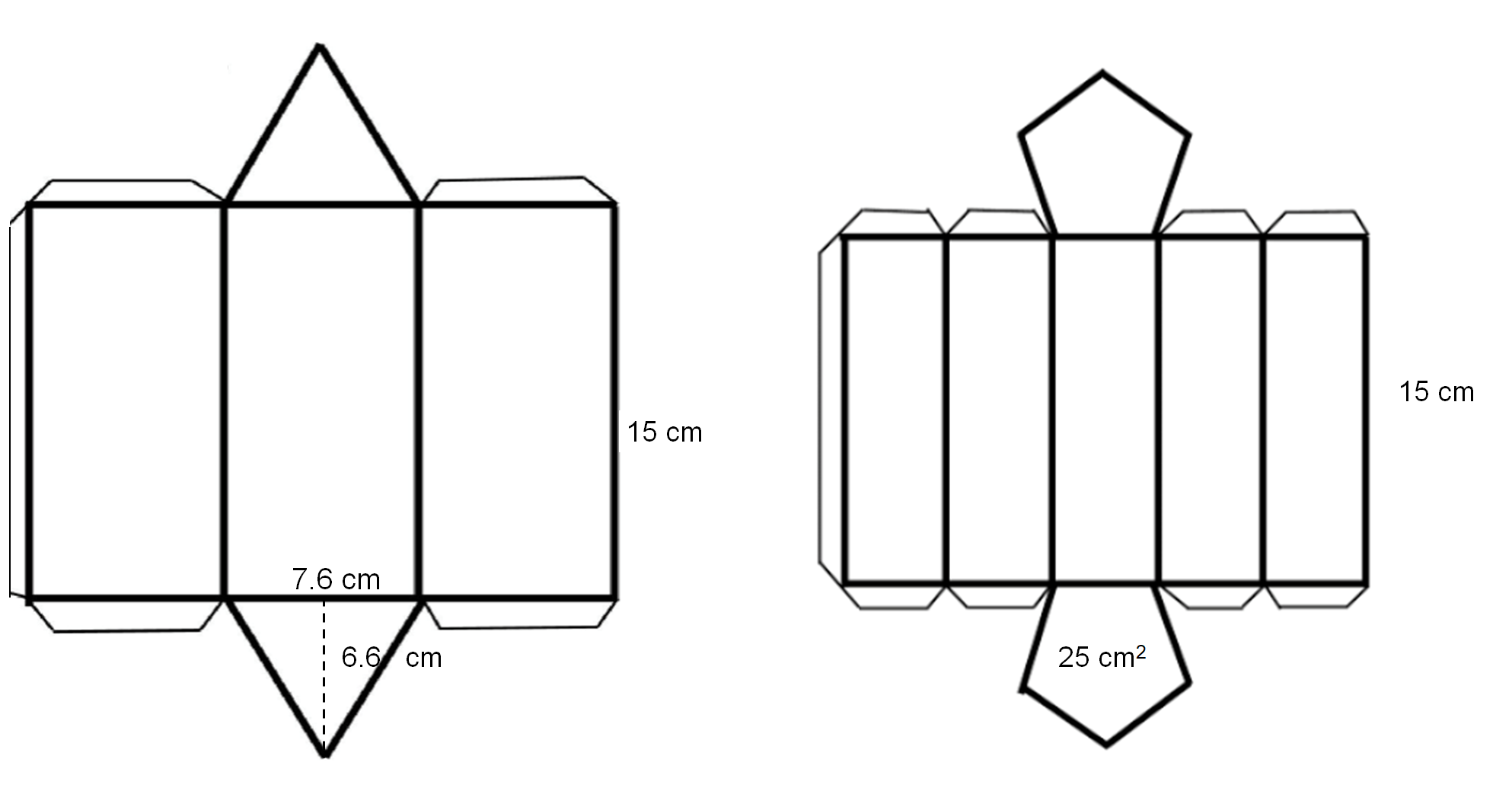
Ya sabes qué son los prismas rectos, cómo son sus desarrollos planos y cuáles son sus características. Asimismo, has relacionado el cálculo del volumen con el desarrollo plano y se mostraron diversas opciones que cumplen con las condiciones dadas.
Los desarrollos planos pueden estar formados por bases cuyas caras sean polígonos regulares, semirregulares o irregulares. El total de figuras del desarrollo plano de un cuerpo debe coincidir con el número de caras del cuerpo geométrico.
Para concluir, analiza lo siguiente:
¿Cómo es el desarrollo plano cuando sus bases son polígonos irregulares?
¿Cuántas caras iguales tienen?
Para responder lo anterior, observa los siguientes prismas.
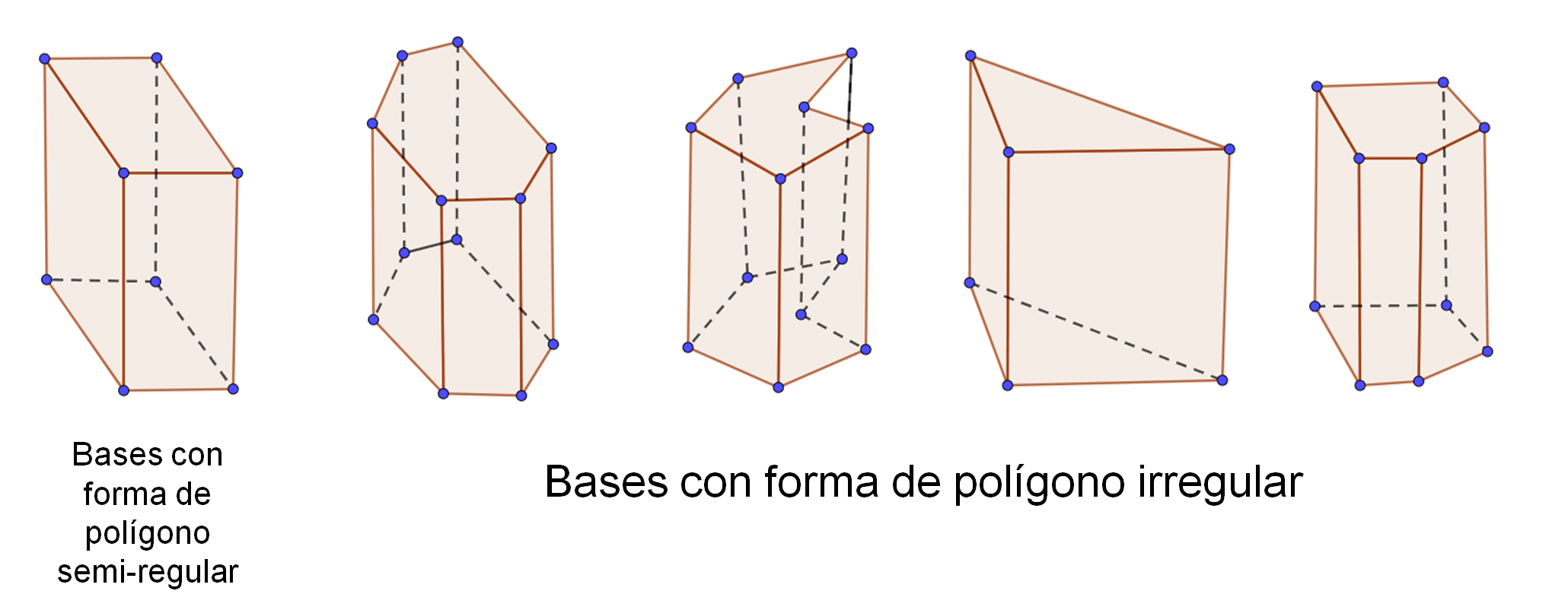
El primero de ellos es un prisma de base rectangular. El polígono que forma las bases es semirregular, ya que no todos sus lados son iguales.
Del segundo al quinto prisma, sus bases son polígonos irregulares. Se puede identificar que las bases son iguales y las caras laterales son rectangulares.
¿Cómo serán sus desarrollos planos?
¿Todos serán diferentes?
¿Cómo son las formas de sus caras laterales?
Analiza el desarrollo plano del prisma de base hexagonal.
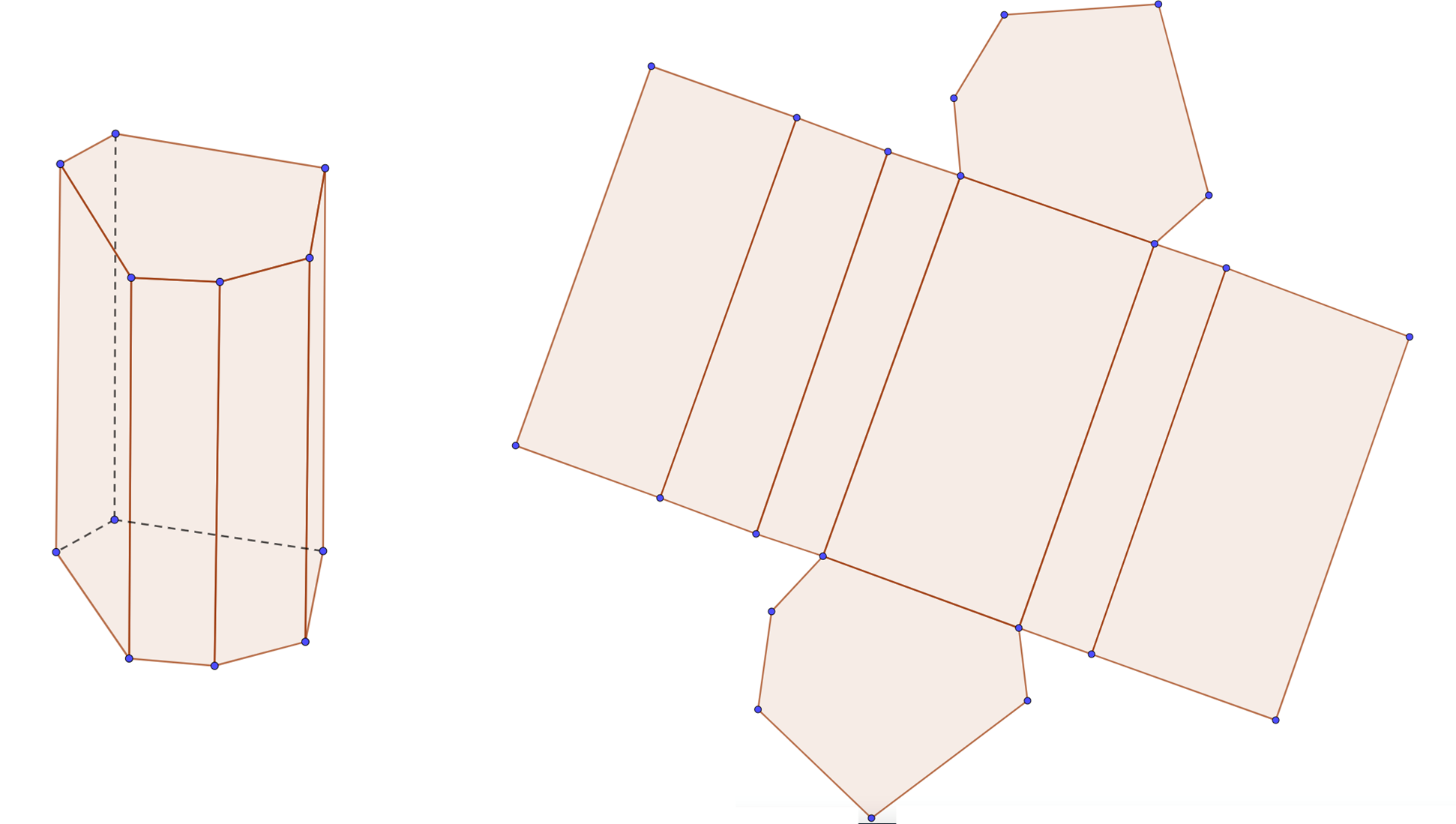
Ambas bases son iguales, tienen forma de hexágono irregular, ya que la medida de sus seis lados es diferente.
Sus caras laterales son 6, en correspondencia con el número total de lados del hexágono. Todas las caras laterales tienen forma de rectángulos con la misma altura, aunque la medida de su ancho es diferente.
Finalmente, analiza de la misma forma el resto de los prismas presentados.
Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.
También, puedes consultar tu libro de texto de Matemáticas de segundo grado, seguramente encontrarás otras actividades que te ayudarán a profundizar en este tema.
El Reto de Hoy:
A la distancia, analiza con tus compañeros y docentes cuáles son los otros 7 desarrollos planos para construir el cubo. Trázalos y arma el cubo. Esta es una excelente manera de validar tus desarrollos planos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/


Login to join the discussion