Décimos, centésimos y milésimos. Las partes de una unidad

Décimos, centésimos y milésimos. Las partes de una unidad

Aprendizaje esperado: notación desarrollada de números naturales y decimales. Valor posicional de las cifras de un número.

Énfasis: determinar fracciones decimales y establecer comparaciones entre ellas a partir de la división sucesiva en 10 partes de una unidad.

¿Qué vamos a aprender?

Aprenderás a determinar fracciones decimales y a establecer comparaciones entre ellas, a partir de la división sucesiva en 10 partes de una unidad.

En el ciclo anterior empezaste a estudiar las fracciones y resolviste algunos problemas, utilizando estos números, por ejemplo: Si tengo una pizza y la voy a compartir con tres amigos más, ¿Cuánto nos toca a cada uno? sencillo, ¿verdad? A cada uno le toca ¼.

En este ciclo escolar, aprenderás más sobre las fracciones, y en eta sesión vas a ver lo que es una fracción decimal.

Para empezar, analiza la siguiente situación y si es posible, llévala a cabo, con ayuda de tu papá o mamá:

Tengo un listón que mide un metro y lo divido en 10 partes iguales.

Recuerda que para que cada parte sea igual debe medir exactamente lo mismo. Puedes utilizar una regla y llevar a cabo la medición.

En este caso, si el metro de listón mide 1 metro = 100 cm y lo divides entre 10.

Cada parte mide 10 centímetros de largo.

Cada una de estas partes la puedes expresar o representar como una fracción a la que llamaremos decimal o como un número al que también podemos llamar decimal.

Cada parte obtenida quedaría representada como 1/10, es decir, un décimo de la unidad.

Ambas formas de escritura nos dicen que esta parte del listón es una de diez partes en que se dividió el metro de listón.

¿Tú crees que se podrá dividir en partes más pequeñas la unidad (el metro de listón) como el décimo de la unidad que obtuviste? ¡Claro que sí!, solo que obtendrías partes aún más pequeñas.

Consulta algún libro que tengas en casa, o en Internet, para saber más del tema.

¿Qué hacemos?

Resuelve el desafió 4 de tu libro de texto, que viene en la página 16. Con ayuda de un adulto sigue las indicaciones que ahí se mencionan y que también te señalamos a continuación.

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/16

1. De un cartoncillo del color que tú prefieras, recorta una tira que mida 1 m de largo para que sea la unidad. Esta tira puede tener de alto 10 centímetros.
   
2. De otro cartoncillo, de un color distinto, recorta una tira que mida 1 m de largo y divídela en 10 partes iguales. Marca y recorta las divisiones.
   
   A cada parte llámala 1 décimo de la unidad o 1/10, o bien, 0.1.
3. De otro cartoncillo, de un color diferente a los anteriores, recorta una tira de 1 décimo de la unidad, es decir del mismo tamaño que una de las partes amarillas anteriores, y divídela en 10 partes iguales. Marca y recorta esas divisiones.
   
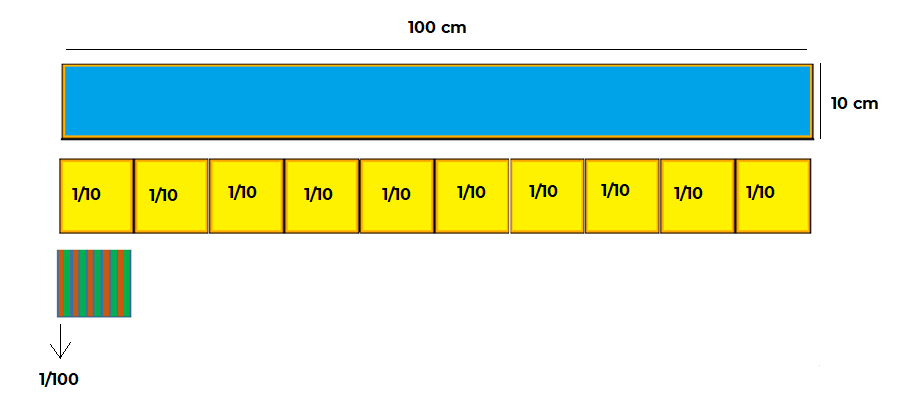
   A cada parte llámala 1 centésimo de la unidad o 1/100, que equivale a 0.01
4. De un último cartoncillo de otro color diferente a los anteriores, recorta una tira de un centésimo de la unidad, es decir del mismo tamaño que una de las partes rojas anteriores y divídela en 10 partes iguales. Marca y recorta las divisiones.

A cada parte se le conocerá como 1 milésimo de la unidad o 1/1000, que también se puede expresar como 0.001

Cómo puedes ver, las últimas partes que recortaste ¡son muy pequeñas!

Contesta las preguntas que vienen en tu libro de desafíos, en la página 17. Utiliza el material que recortaste:

¿Cómo podrías saber la respuesta?

Para saberlo, puedes emplear la técnica de la sobreposición, en este caso, debes colocar encima de la tira azul, las partes que quieres comparar:

• ¿Cuántos cuadros amarillos caben en la tira azul? Verás que, en la tira azul, caben 10 cuadros amarillos, es decir en el metro, que es nuestra unidad, caben 10 décimos.
• ¿Cuántas tiritas rojas, caben en un cuadro amarillo? Caben 10, es decir, en un décimo caben 10 centésimos.
• ¿Cuántos milésimos caben en un centésimo? Tal vez, sea un poco difícil, superponer las tiritas, pero si analizas la situación, verás que en un centésimo caben en 10 milésimos.

Continúa con la siguiente pregunta:

Para encontrar esta respuesta toma una tira de un décimo y otra de un centésimo. ¿Cuál es más grande? Claro ¡un décimo!

Ahora trata de dar respuesta a las preguntas que faltan.

Si tienes alguna dificultad para dar respuesta a las preguntas, anota tus dudas, para que cuando puedas comunicarte con tu maestra o maestro, le pidas que te ayude a resolverlas.

Para concluir, lee con atención lo siguiente que resume lo que acabas de aprender. Analiza también el esquema que se presenta.

• Un milésimo es la décima parte de un centésimo.
• Un centésimo es la décima parte de un décimo.
• Un décimo es la décima parte de la unidad.

El reto de hoy:

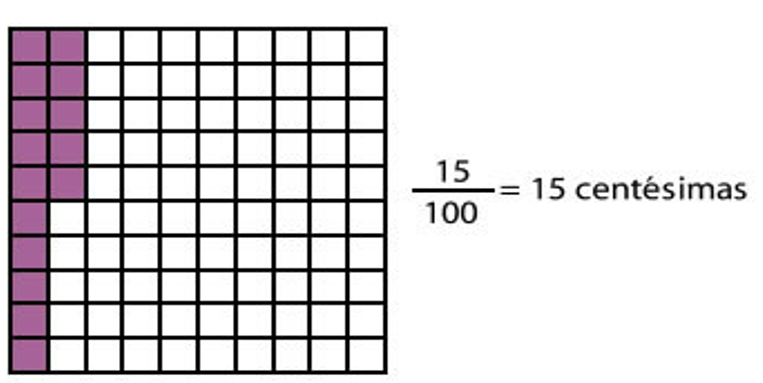
Representa por medio de cuadriculas las siguientes fracciones:

50/100

5/10

500/1000

Fíjate en el ejemplo y toma en cuenta que en esta figura hay décimos, centésimos y milésimos.

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/