De los babilónicos a la actualidad

De los babilónicos a la actualidad

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: resolver problemas mediante el planteamiento y resolución de sistemas de ecuaciones lineales con dos incógnitas utilizando el método de sustitución.

¿Qué vamos a aprender?

Conocerás la Historia de los sistemas de ecuaciones lineales. Además, continuarás con la resolución de problemas mediante el planteamiento de sistemas de dos ecuaciones lineales con dos incógnitas, utilizando el Método de Sustitución, en esta ocasión será un caso especial; cuando el despeje de alguna literal es un cociente.

¿Qué hacemos?

Para empezar, conoce un poco de la Historia de los sistemas de ecuaciones lineales, esto te permitirá comprenderlas, entenderlas y disfrutarlas más.

Es emocionante saber que a veces los pensamientos son semejantes a los de los grandes matemáticos y matemáticas de la Historia. Muchas de las grandes ideas matemáticas que forman parte de nuestro día a día, han surgido de las necesidades de cada civilización, de superar retos que enfrentaban y que los obligaron a pensar de maneras distintas.

Los sistemas de ecuaciones lineales fueron resueltos por los babilonios, desde el año 600 a. c. Aquella civilización llamaba a las incógnitas con palabras tales como longitud, anchura, área, o volumen, sin que entonces, tuvieran relación con problemas de medida.

Un ejemplo tomado de una tablilla babilónica plantea la resolución de un sistema de ecuaciones en los siguientes términos:

La antigua civilización griega también resolvía algunos sistemas de ecuaciones, pero utilizando métodos geométricos.

Thymaridas de Paros encontró una regla para resolver un determinado sistema de “n” ecuaciones con “n” incógnitas. La regla se hizo tan conocida que adoptó el título de la Flor de Thymaridas.

Diophante, resolvió también problemas en los que aparecían sistemas de ecuaciones, pero transformándolos en una ecuación lineal.

El libro: El arte matemático, del autor chino desconocido (siglo II a.c), contiene algunos problemas en donde se resuelven ecuaciones. En ellos se encuentra un esbozo, del método actual, para resolver sistemas de ecuaciones lineales.

A continuación, analiza dos situaciones-problema que pueden resolverse con el método de sustitución.

Situación-problema 1

El perímetro del rectángulo anaranjado es igual a 64 cm. La diferencia entre las medidas de la base y la altura son 6 cm.

¿Cuál es la medida de la base y la altura de dicho rectángulo?

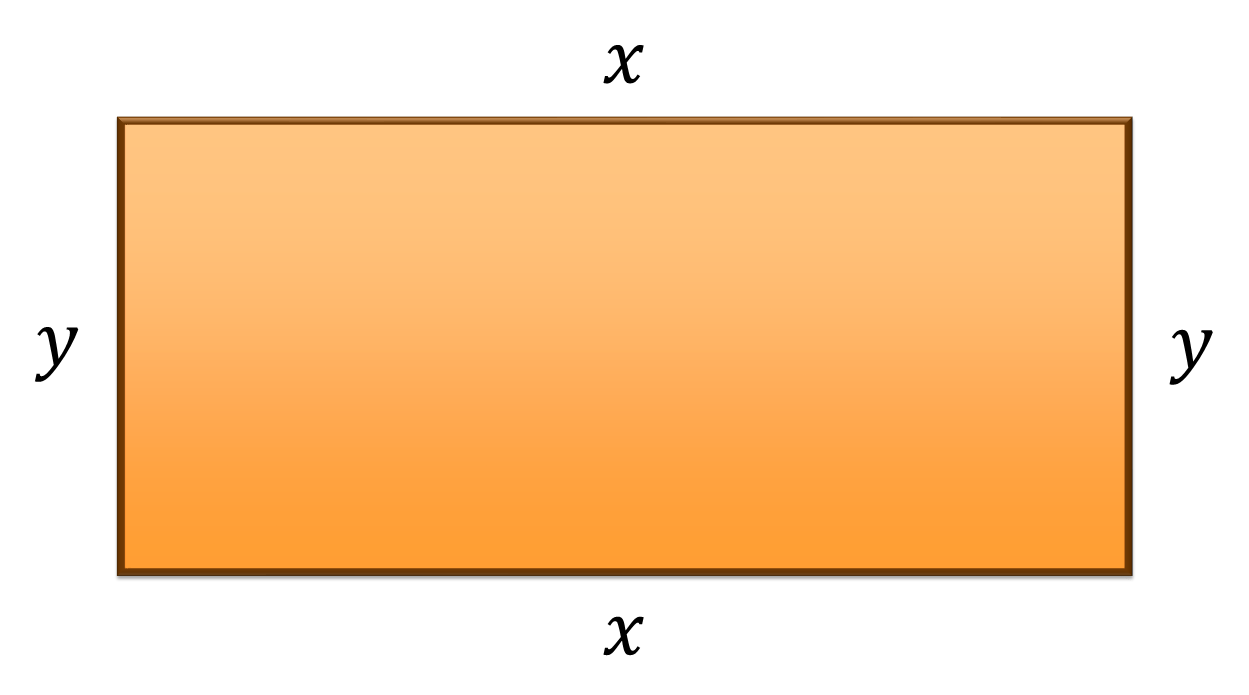
Considera que la medida de la base es mayor que la altura y la diferencia entre ambas es igual a 6.

Como se muestra en la representación del rectángulo, cada lado está relacionado con una incógnita que te ayudará a resolver la situación-problema.

Analiza las condiciones del problema:

• Se sabe que el rectángulo tiene dos pares de lados iguales.
• “x” representa la medida de la base del rectángulo y es mayor que la medida de la altura.
• “y” representa la altura del rectángulo.
• La diferencia de medidas entre la base y la altura es de 6 cm.

Ahora, plantea el sistema de ecuaciones que modela la situación-problema.

Se sabe que para obtener el perímetro de un rectángulo se puede usar la expresión:

2b + 2h = perímetro

La fórmula anterior se puede traducir de la siguiente forma:

Si se suman dos veces la longitud de la base y dos veces la longitud de la altura, se obtiene el perímetro de un rectángulo. La base será “x” y a la altura “y”, la expresión anterior queda de la siguiente forma.

“x” es igual a “b”, medida de la base.

“y” es igual a “h”, medida de la altura.

Planteamiento del sistema de ecuaciones:

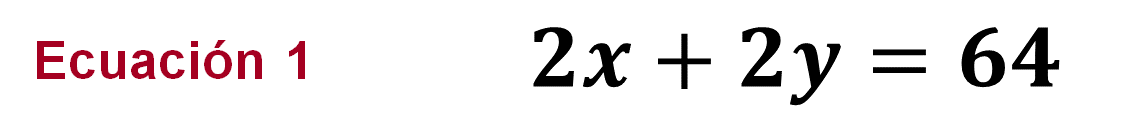
Donde “x” representa la medida de la base del rectángulo, y “y” representa la medida de la altura del rectángulo.

A partir de saber que la medida de la base es mayor que la altura y la diferencia entre estas medidas es igual a 6, se plantea la segunda ecuación. Por ello se tiene que la ecuación 2 es:

En la ecuación 2, se representa la diferencia entre la medida de la base y la altura del rectángulo: 6 cm.

Entonces el sistema de ecuaciones queda integrado como:

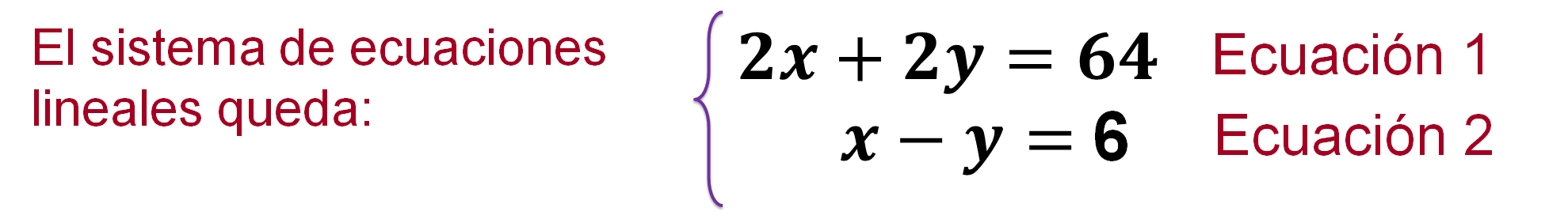
Una vez establecido el sistema de ecuaciones, puedes decidir cuál de las incógnitas despejar para iniciar la resolución de la situación planteada. Tienes 2 ecuaciones con dos incógnitas cada una, por esta situación, puedes seleccionar con cuál de las 4 posibilidades deseas iniciar.

En esta ocasión, empieza con despejar la incógnita “x” de la ecuación 2.

Se sabe que el proceso de despejar una incógnita implica utilizar distintos procedimientos algebraicos hasta lograr “aislar” una incógnita en el primero o segundo miembro de una ecuación con la intención de conocer el valor algebraico de la misma. Al despejar la incógnita podrás sustituir su equivalente algebraico en la ecuación que no has utilizado.

Resolución del sistema de ecuaciones:

Despeja la incógnita “x” de la ecuación 2. Para despejar la incógnita “x”, utilizarás las propiedades de los números y las operaciones, aplica el inverso aditivo de “-y”, que es “y”, y suma en ambos miembros de la ecuación.

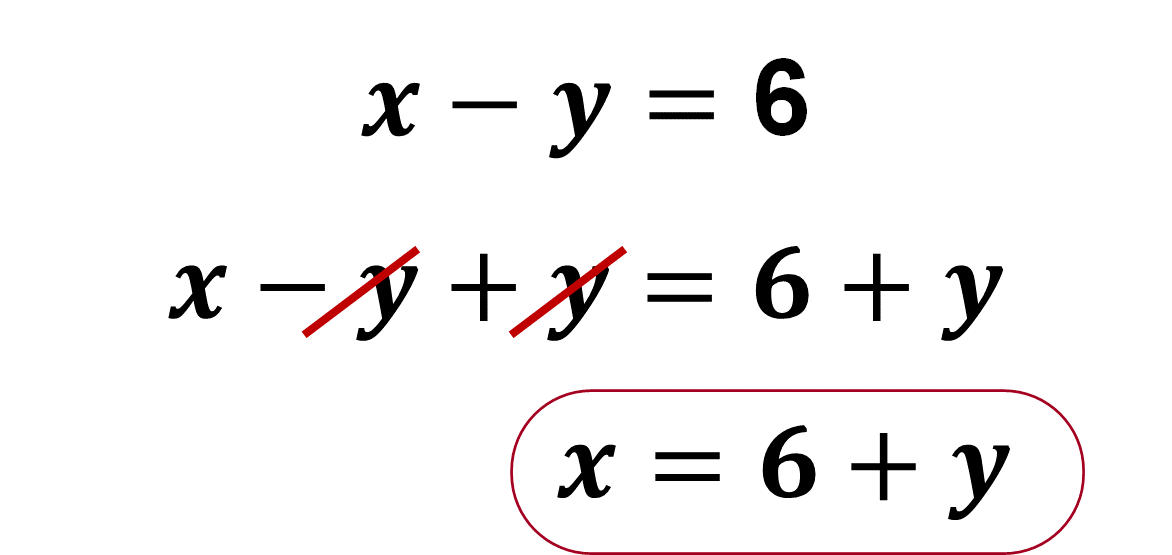
Este despeje será sustituido en la Ecuación 1:

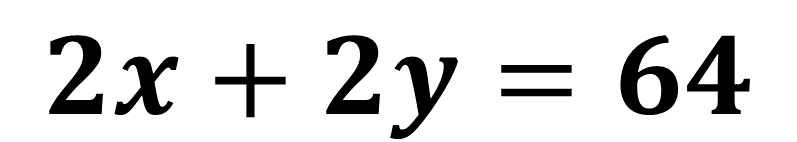
Queda de la siguiente manera:

En el lugar de la incógnita “x”, anota el valor de la igualdad del despeje de “x” en la Ecuación 1.

Se resuelve 2(6+y) de la ecuación para obtener:

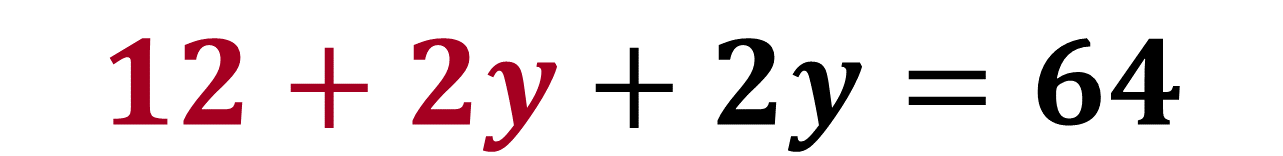
Utiliza las propiedades de los números y las operaciones:

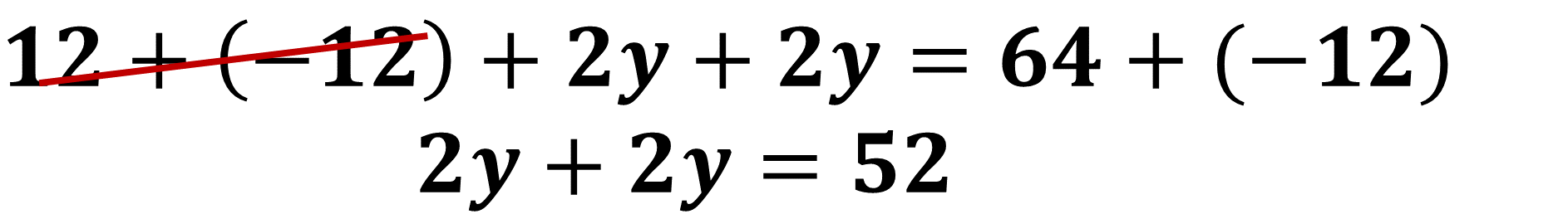
Reduce términos semejantes sumando aquellos términos que tienen la misma parte literal y aquellos que carecen de ella:

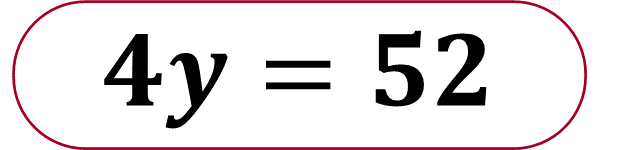
Aplica el inverso multiplicativo de 4:

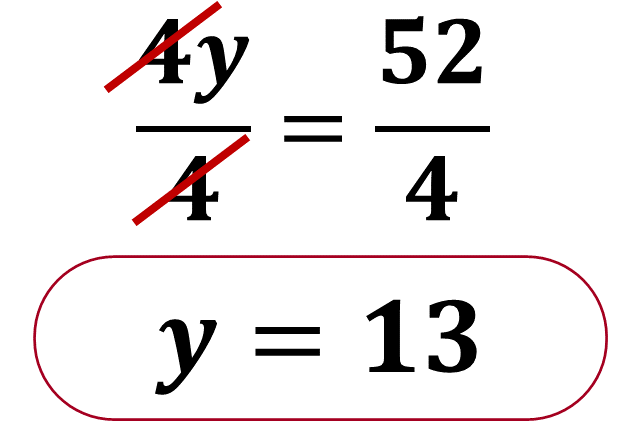
“y” representa la medida de la altura del rectángulo anaranjado.

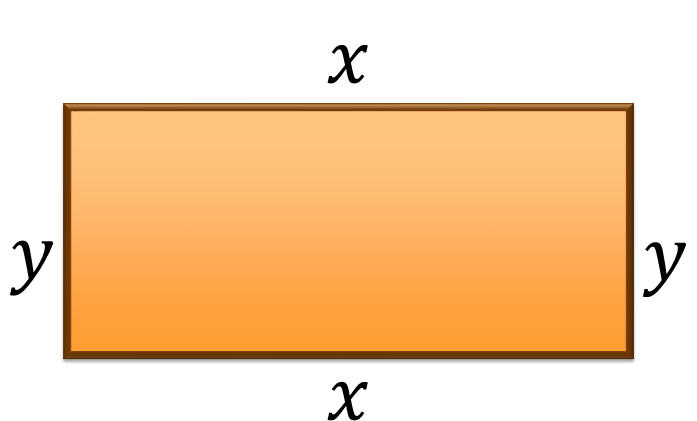
Ahora que ya sabes que la altura del rectángulo es de 13 cm, determinemos la medida de su base. Considera la información inicial del problema en el que se menciona que la medida de la base es mayor que la altura y la diferencia entre estas medidas es igual a 6.

y=13

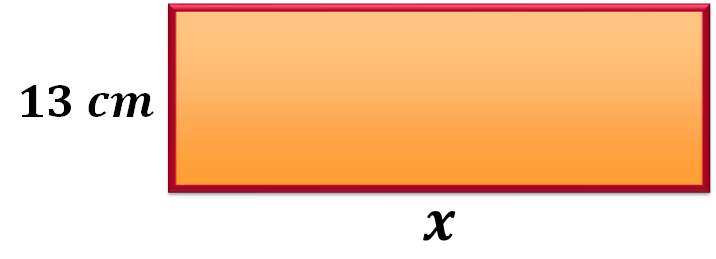
Sustituye el valor de “y” en la Ecuación 1:

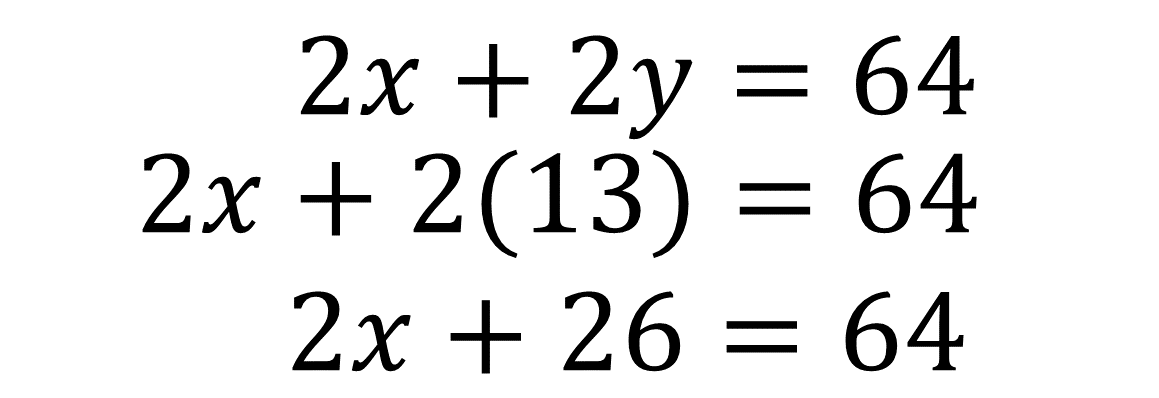
Utiliza las propiedades de los números y las operaciones para resolver la ecuación:

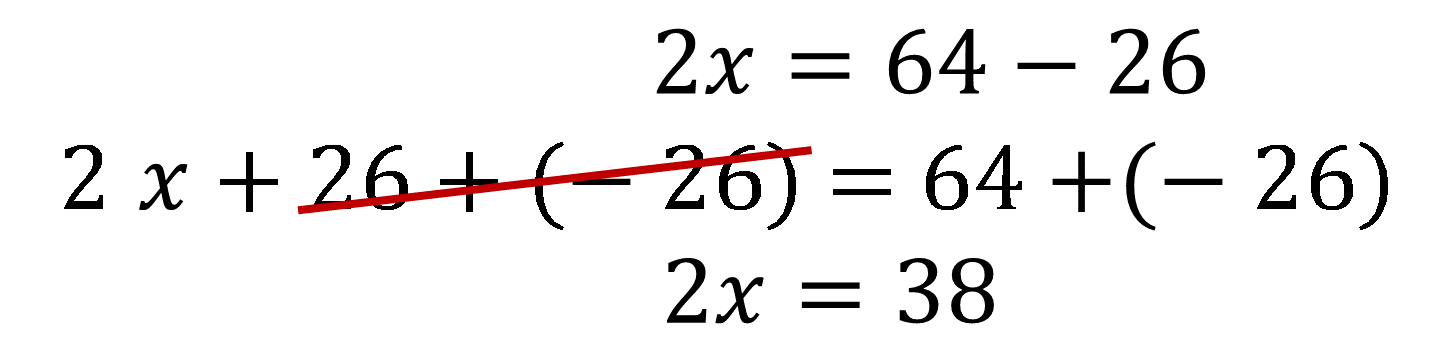
Aplica el inverso multiplicativo:

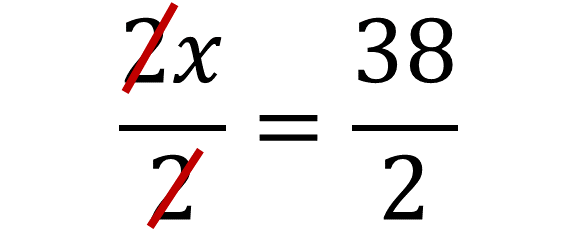
Obtén el valor de la incógnita “x” y listo:

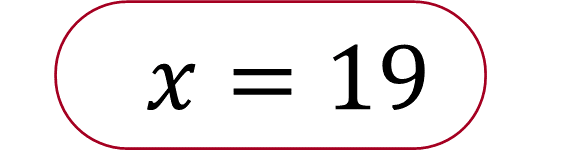
Por lo tanto, x = 19

Has encontrado el valor de “x”.

Ahora vas a corroborar los valores numéricos de las incógnitas que obtuviste. Esto con la finalidad de asegurar que sean correctos.

Comprobación de las soluciones:

Se sabe que:

x = 19

y = 13

Sustituye ambos valores en la Ecuación 1:

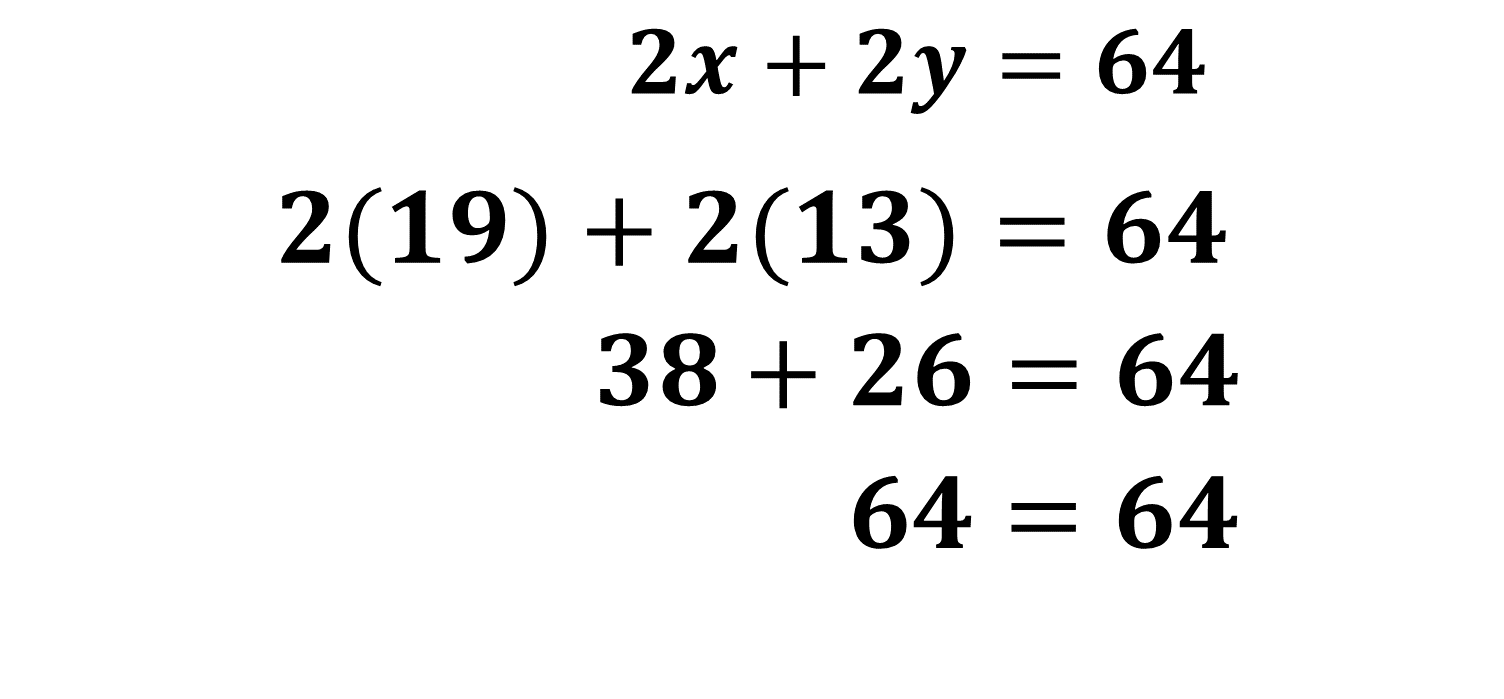
Observa que en ambos lados de la igualdad tienes 64, por lo tanto, son iguales. Es importante que los resultados sean comprobados en ambas ecuaciones del sistema.

Sustituye ambos valores en la Ecuación 2:

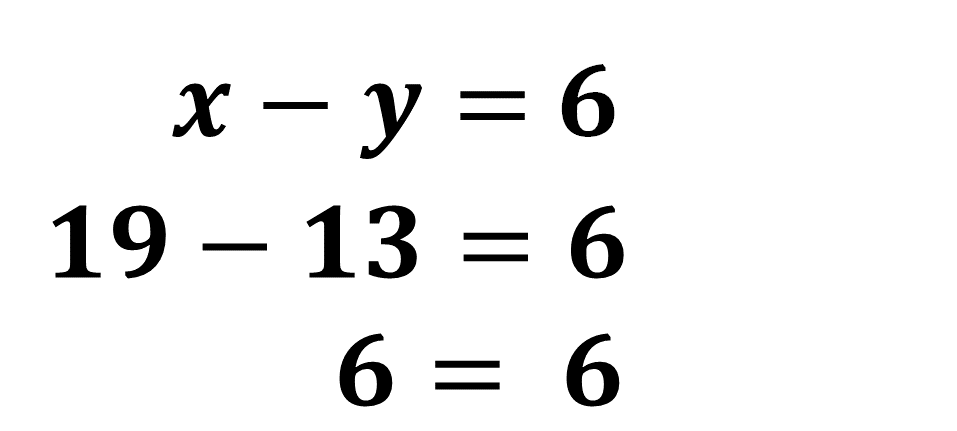
Obtienes 6 en ambos lados de la igualdad. Por lo tanto, son iguales.

Recuerda que, si tienes dudas, es importante anotarlas, para después consultar en tu libro y preguntarles a tus docentes de matemáticas.

Ahora resuelve otra situación-problema mediante el planteamiento y resolución de un sistema de ecuaciones con el método de sustitución, observando una situación especial.

Situación-problema 2

Ruty trabaja en una tienda de accesorios para computadoras y ofrece unidades de almacenamiento de datos con entrada USB, en varios modelos y capacidades.

Ruty vendió 4 dispositivos de almacenamiento masivo de 2 Gb y 8 de 4 Gb, en total cobró $2 800. Por la tarde, vendió 16 de 2 Gb y 24 de 4 Gb, por ellos cobró $9 280.

¿Cuánto cuesta cada dispositivo?

Con los datos que plantea el problema:

¿Es posible establecer sistemas de ecuaciones lineales con dos incógnitas?

¿Qué valores necesitamos conocer?

Observa si se puede plantear un sistema de ecuaciones lineales con dos incógnitas.

Para encontrar el costo de cada dispositivo es necesario plantear un sistema de dos ecuaciones.

• Escribe la ecuación que describe la situación “vendió 4 dispositivos de almacenamiento masivo de 2 Gb y 8 de 4 Gb, en total cobró $2 800”.
• Escribe la ecuación que describe la situación “vendió 16 de 2 Gb y 24 de 4 Gb, por ellos cobró $9 280”.

Analiza cómo puedes resolver el problema relacionando las dos ecuaciones.

Una vez que realizas el análisis de la información del problema, comienza a establecer el sistema de ecuaciones para solucionar la situación planteada.

Planteamiento del sistema de ecuaciones:

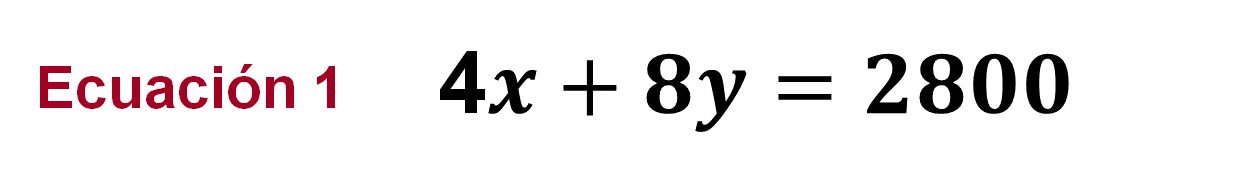
Donde “x” representa la cantidad de dispositivos masivos de 2 Gb y “y” representa la cantidad de dispositivos masivos de 4 Gb.

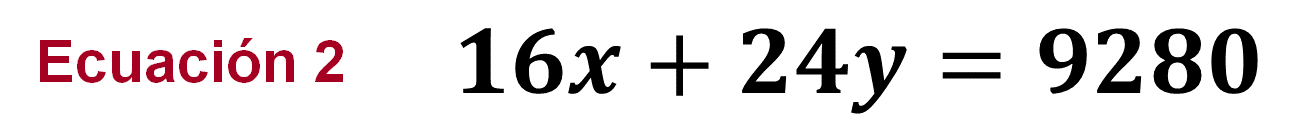
En esta segunda ecuación, se considera “16x” que representa la cantidad de dispositivos masivos de 2 Gb y “24y” representa la cantidad de dispositivos masivos de 4 Gb.

Entonces el sistema queda de la siguiente manera:

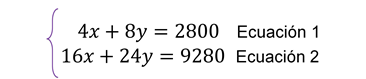
Resolución del sistema de ecuaciones.

Comienza a resolver el sistema de ecuaciones despejando la incógnita “y” de la ecuación 1. Utiliza las propiedades de los números y las operaciones y suma en ambos miembros de la ecuación el inverso aditivo de 4x, de este modo tenemos:

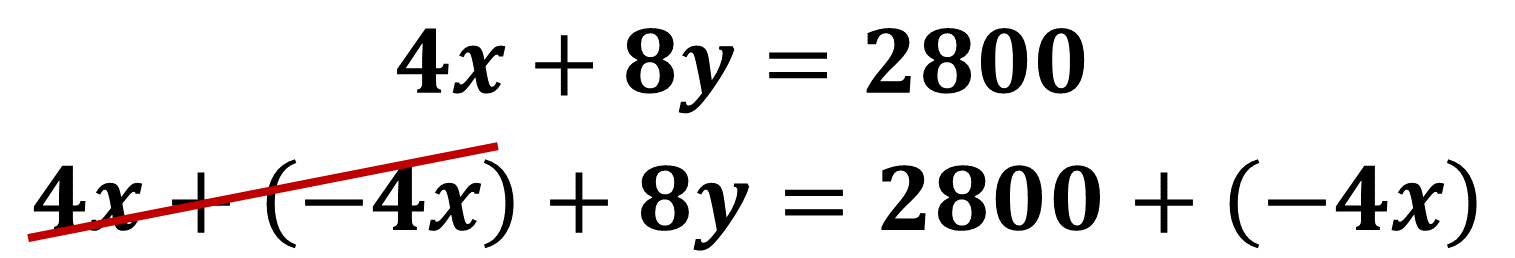
El resultado de reducir términos semejantes es:

Aplica el inverso multiplicativo de 8 en ambos miembros de la igualdad:

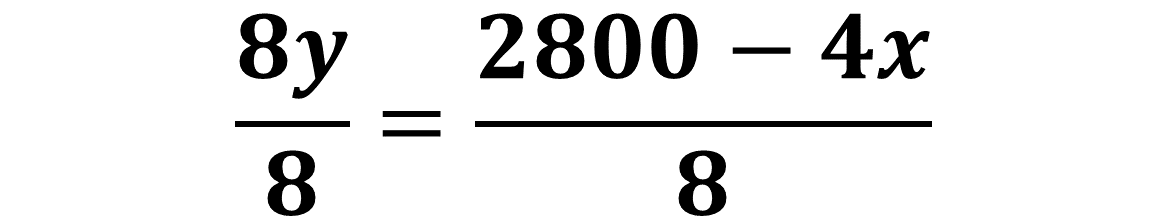
Obtienes:

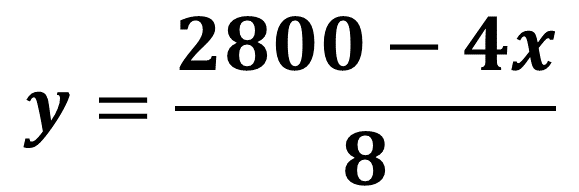
Se sustituye “y” en la Ecuación 2:

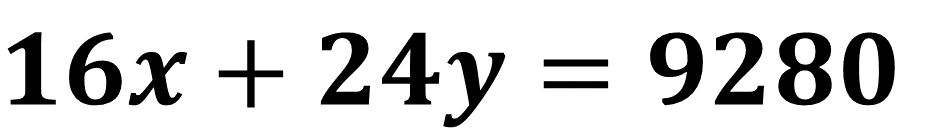
Queda de la siguiente manera:

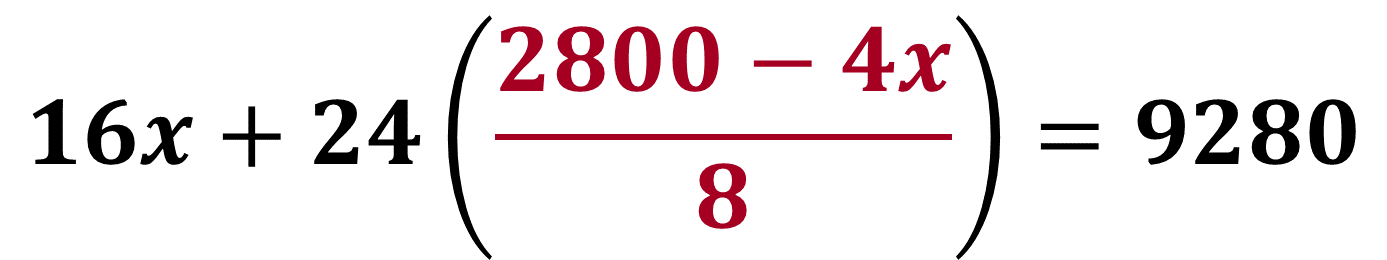
Ahora resuelve el cociente 2800 - 4x/8 de la ecuación. Al dividir 2800 entre 8, se obtiene como cociente 350, y 4x entre 8 puede reducirse a la fracción un medio de x.

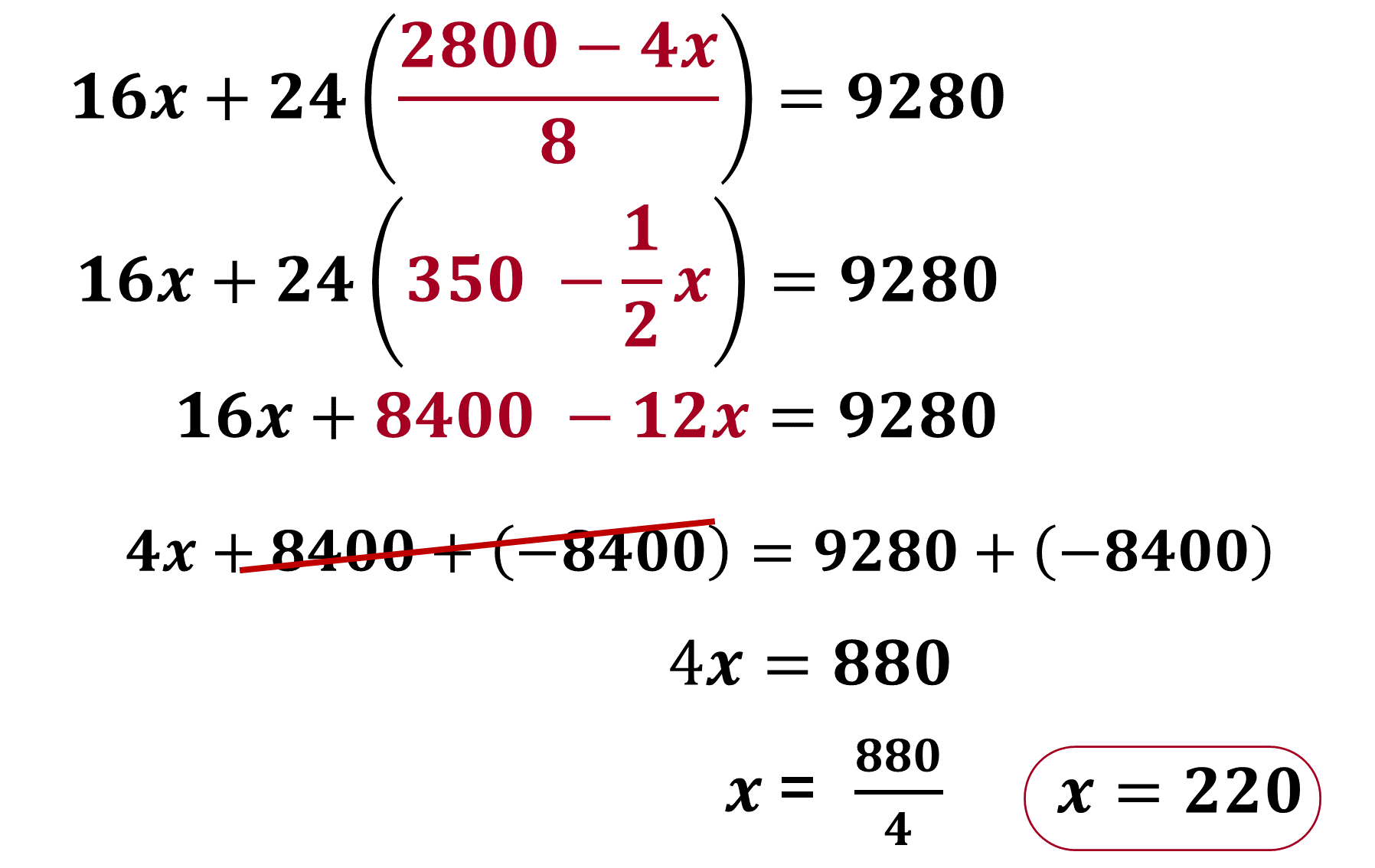
Se sabe que: x = 220, que representa la cantidad de dispositivos de 2 Gb.

Ahora que ya sabes que los dispositivos masivos de 2 Gb cuestan: 220 pesos. Te falta conocer el costo de los dispositivos masivos de 4 Gb.

Con la respuesta anterior, puedes determinar el costo desconocido, sustituyendo el valor numérico de “x” en la ecuación 1, en la que tienes:

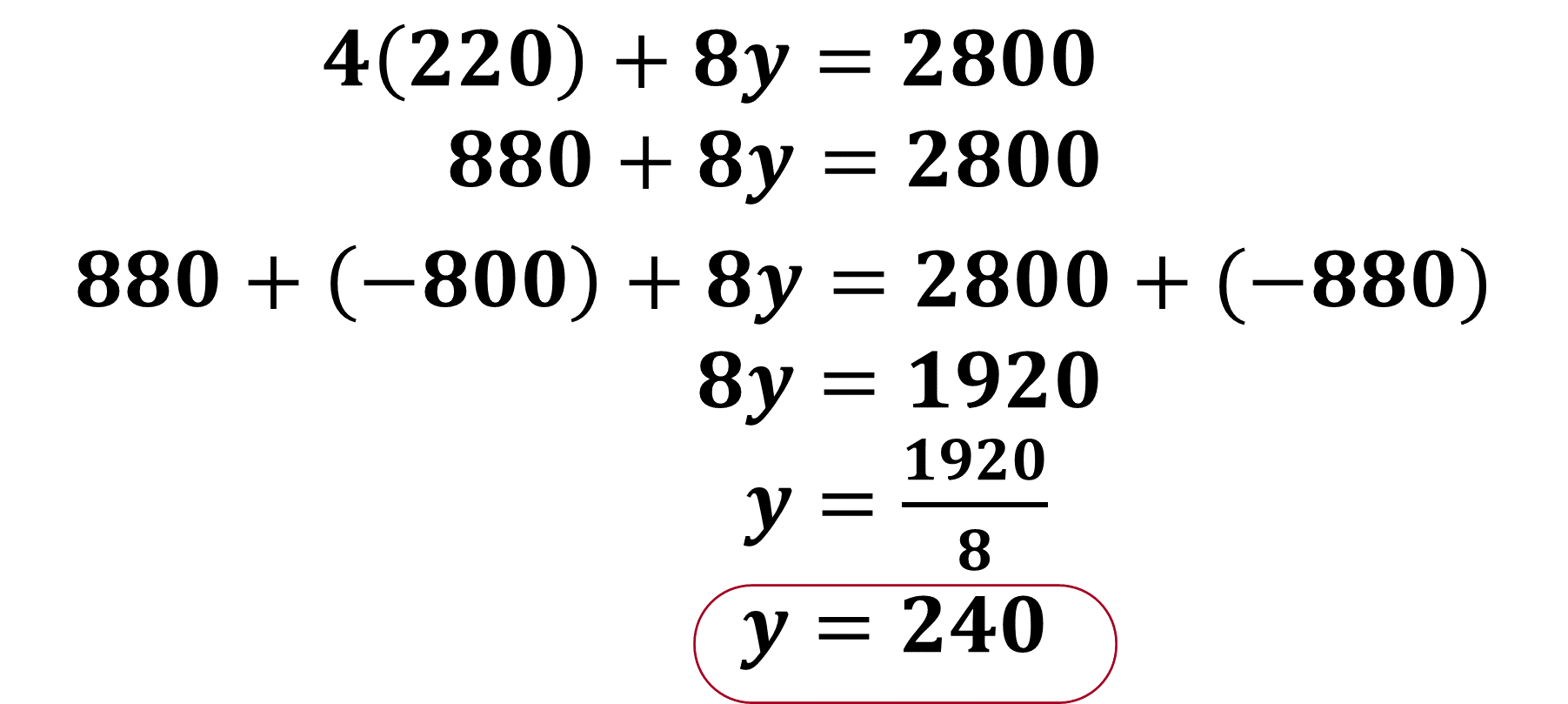
Por lo tanto, y = 240. Se sabe que “y” representa la cantidad de dispositivos masivos de 8Gb.

Es momento de comprobar los valores numéricos que obtuviste de las incógnitas.

Comprobación de soluciones.

Se sabe que:

x = 220

y = 240

Sustituye ambos valores en la Ecuación 1:

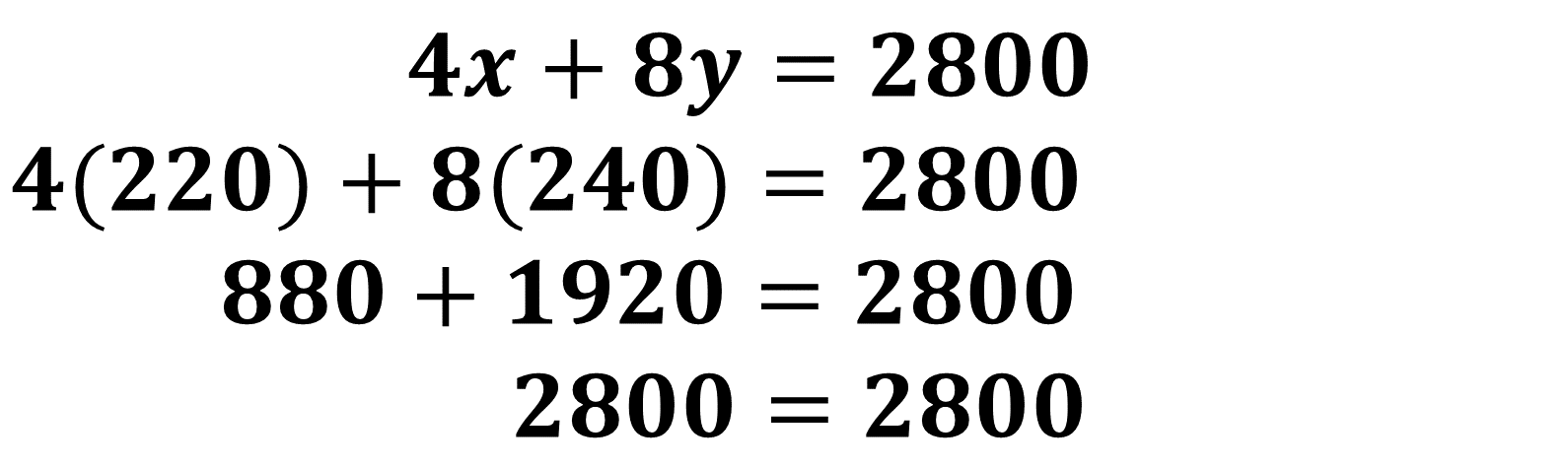
Realiza la suma de los valores numéricos, obteniendo 2800 de ambos lados, por lo tanto, son iguales.

Ahora, sustituye ambos valores en la Ecuación 2:

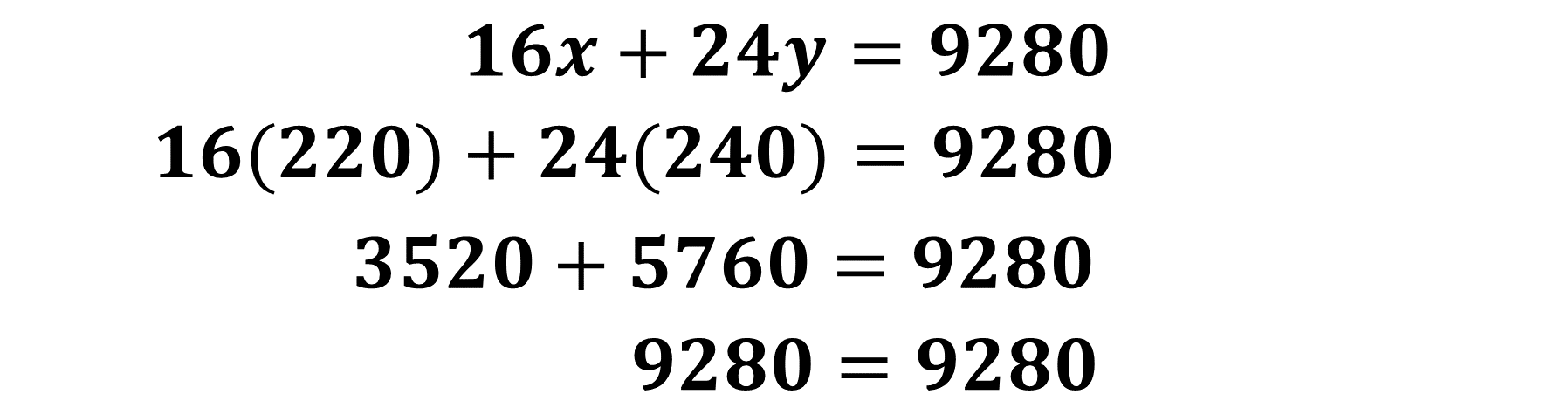
Resuelve la suma en la que se obtiene como resultado 9280 en ambos lados de la ecuación, y por lo tanto son iguales.

Por lo tanto, los valores de las incógnitas, obtenidos mediante la resolución del sistema de ecuaciones, son correctos. Has resuelto la situación-problema, utilizando el método de sustitución.

Hoy has trabajado un caso especial: en el que resolviste un problema planteando un sistema de dos ecuaciones lineales con dos incógnitas, cuando el despeje de alguna literal es un cociente.

Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo aprendido.

Puedes consultar tu libro de Texto de Matemáticas, de segundo grado; busca el tema de sistemas de ecuaciones, y profundiza con los ejemplos propuestos en él.

El reto de hoy:

Encuentra el sistema de dos ecuaciones lineales con dos incógnitas que resuelve el siguiente problema:

Tanya compró en oferta tres pelotas grandes y dos chicas por $16; mientras que Lulú compró también en oferta cinco pelotas chicas y dos grandes por $18.

¿Cuál de los siguientes sistemas de ecuaciones permite resolver correctamente el problema?

A continuación, se plantean tres sistemas de ecuaciones con los que se pretende resolver este problema. Realiza las operaciones correspondientes y elige el inciso correcto.

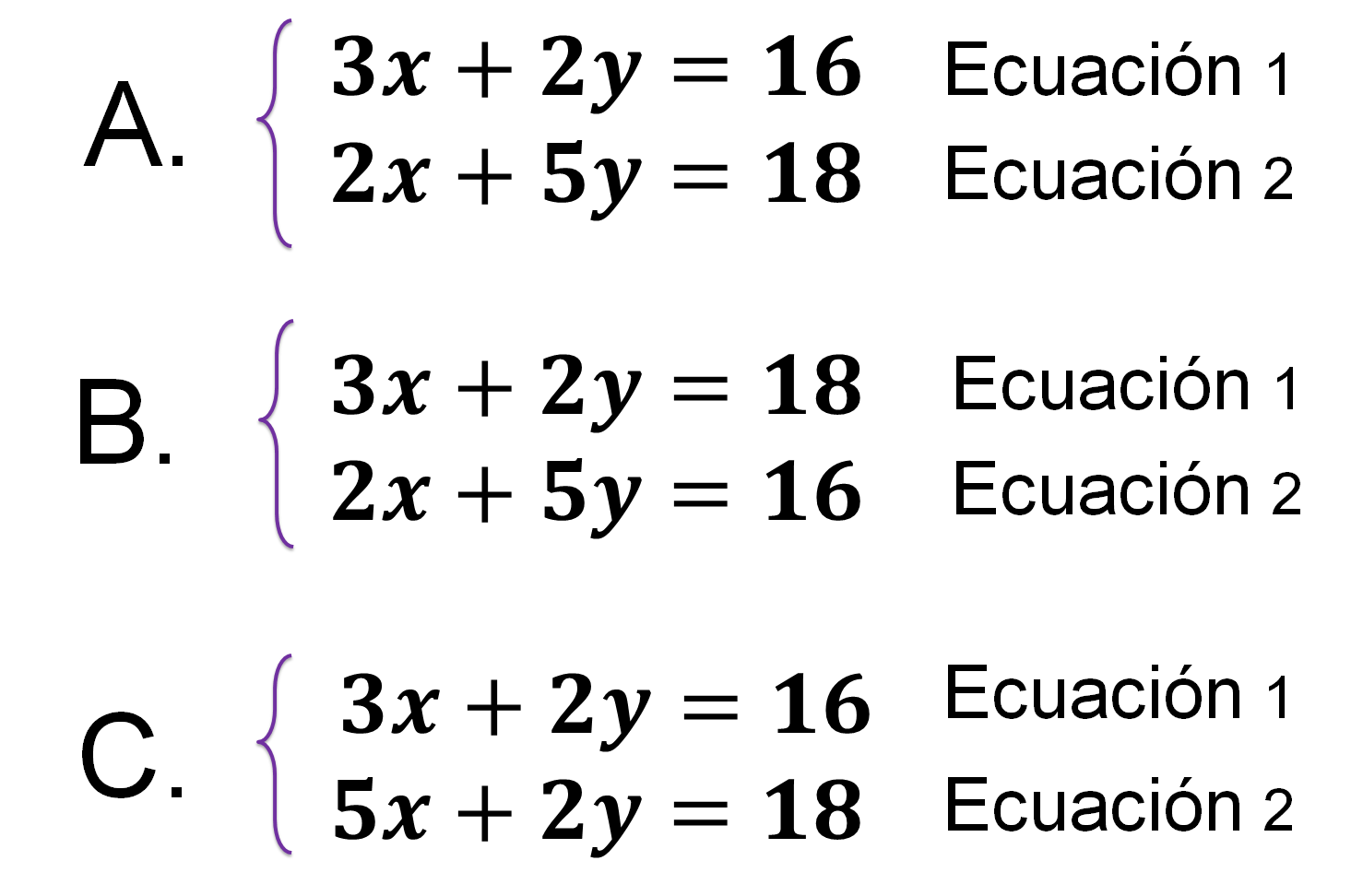
¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/