De diferentes maneras
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27
De diferentes maneras
Aprendizaje esperado: identificación de escrituras equivalentes (aditivas, mixtas) con fracciones. Comparación de fracciones en casos sencillos (con igual numerador o igual denominador).
Énfasis: usa diversas formas aditivas para representar una fracción mixta.
¿Qué vamos a aprender?
Aprenderás sobre la interpretación de las fracciones equivalentes en su denominación mixta por medio del ejercicio práctico.
¿Qué hacemos?
Es momento de empezar por medio de un juego de 12 cartas, donde gana la carta que represente mayo cantidad por ejemplo entre:
1/2
10/8
El 10 es mayor que 8 eso significa que la fracción representa más de un entero y por ende 1 es menor que el dos, así que es menos de un entero. Siguiente ejercicio:
5/4
4/4
En esta es evidente que 5 cuartos es mayor que 4 cuartos. La siguiente es:
16/8
6/2
En este caso las dos representan más de un entero, por lo cual es necesario convertirlas a números mixtos para que sea más fácil compararlas. De acuerdo, la segunda equivale a 3 enteros, porque con 6 mitades se forman 3 enteros, en el primer caso son 2 enteros porque un entero tiene 8 octavos, así que 16 octavos son dos enteros. Siguiente:
9/2 que en fracción mixta sería 4 1/2 porque con 8 mitades o medios se forman 4 enteros y sobra un medio, entonces son 4 enteros un medio.
11/4 que equivale a 2 3/4 porque cada entero tiene 4 cuartos, entonces con 8 cuartos se forman 2 enteros y hay 3 cuartos más.
En este caso, ¿Qué fracción gana? Anota la respuesta en tu cuaderno.
Las siguientes fracciones son:
7/4
2/8
Ganas 7/4 porque es más de un entero y 2/8 es menos de un entero. Las siguientes fracciones son estas:
12/8
8/2
Ahora ambos son más de un entero porque el numerador es mayor al denominador, entonces otra vez hay que convertirlas en mixtas. Con 8 octavos se forma un entero 4 octavos, 1 4/8 la otra fracción es como decir 8 mitades y fácilmente 8 mitades o medios forman 4 enteros, así que gana la segunda fracción.
Este juego tuvimos diferentes fracciones que te permitieron repasar, también había fracciones que eran equivalentes como 2/4, 1/2 o 4/8 y también fracciones impropias como 4/2 o 10/8 que son las que tienen el numerador mayor que el denominador. Las fracciones impropias originan números mixtos.
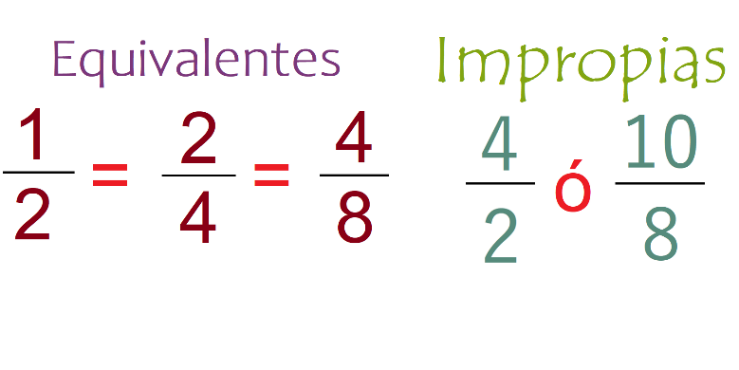
En otras sesiones ya habías visto que las fracciones impropias se pueden convertir en números mixtos, es decir, números que se expresan con un número entero y una fracción común, ¿Lo recuerdas?
Observa la siguiente fracción.
7/4
Esta es una fracción impropia, porque su numerador 7 es mayor al denominador 4 ahora debes convertirla en número mixto. ¿Cuántas de esas 7 partes necesitas para formar un entero?
Exacto como son cuartos, necesitas 4 partes para formar un entero y, ¿Cuántos cuartos me sobran?
7 – 4 = 3
Pero, ¿3 alcanzan para formar un nuevo entero?
No, porque necesitas 4 eso quiere decir que con 7/4 formas un entero y tienes tres cuartos más, esto es lo mismo que 1 ¾
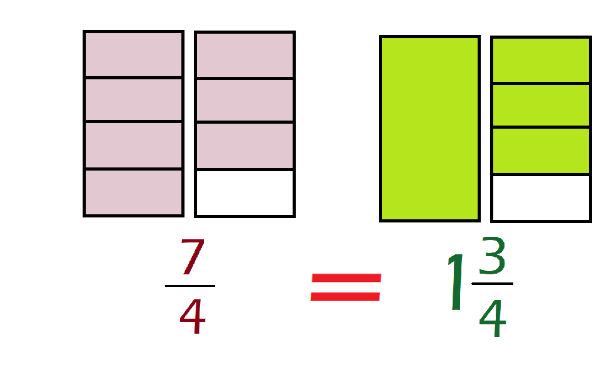
Aquí puedes ver gráficamente cómo es que 7 cuartos forman un entero más 3 cuartos. Así de rápido y fácil obtienes el número mixto, porque tiene un número entero y uno fraccionario.
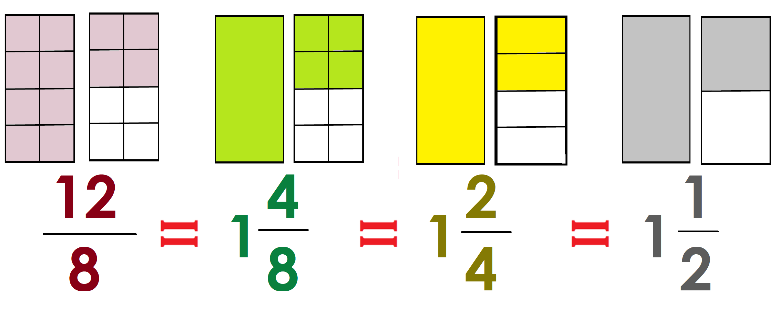
Ahora la fracción 12/8 ¿Cómo la convertirías en mixta?
Primero 12 – 8 = 4
Es decir, necesitas 8 secciones para formar un entero, 12 – 8 = 4 y 4 ya no alcanzan para hacer otro entero entonces queda 1 4/8
Lo hiciste muy bien, observa la imagen donde está representada la fracción 12/8 como ven se completa un entero y 4 octavos de otro entero, pero también es lo mismo que 1 2/4 y todavía puedes encontrar otra expresión que sea equivalente a las anteriores, y es 1 1/2 porque si recuerdas 1/2, 2/4 y 4/8 son fracciones equivalentes.
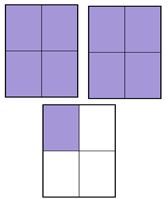
Ahora en el siguiente dibujo buscarás la fracción que representa el dibujo y luego, escribirás la fracción mixta en tu cuaderno.

La fracción impropia son los segmentos.
1, 2, 3, 4, 5, 6 y 7 y como están divididos a la mitad, son medios. La fracción sería 7/2
Y el número mixto de la siguiente fracción 31/2
Entonces serían 3 enteros y 1/2
Observa el dibujo:
Al contar las secciones coloreadas observas que son 9 y como está dividida en 4, la fracción es:
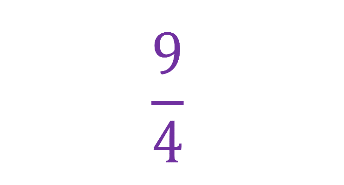
La fracción impropia sería 9/4 ¿Y el número mixto?
Fácil, se observan 2 enteros completos y 1/4
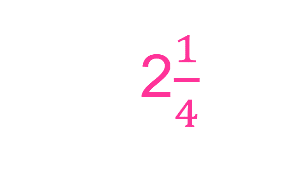
Eso quiere decir que el número mixto es 2 ¼ esto te servirá para resolver el siguiente planteamiento que se encuentra en tu libro de texto página 111 de Desafíos Matemáticos, Tercer Grado.

La imagen dice lo siguiente:
En la ferretería de Pedro se vende pintura en recipientes de diferentes tamaños. Hay de 1/4 de litro, 1/2 litro, 1 1/4 litros, 2 litros y de 3 1/2 litros. Luis va a pintar su cuarto y calcula que necesita 7 3/4 litros de pintura. ¿Qué recipientes puede comprar de manera que no le sobre pintura? ¿Cuál opción es más conveniente?
Escribe en tu cuaderno la respuesta correcta.
A continuación, puedes leer como lo resolvió una compañera tuya del tercer grado de primaria.
“Querido compañero (a) mi nombre es Alondra y quise adelantarme así que resolví el desafío 51 por ello puedes observar si estoy bien o mal.
Para obtener la respuesta vi que lo que necesitaba Luis estaba expresado en cuartos entonces usé el recipiente de 1 1/4.
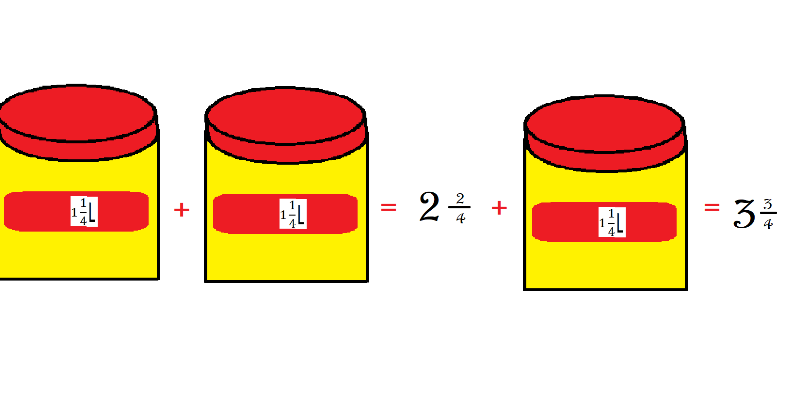
Lo fui sumando así 1 1/4 + 1 1/4 = 2 2/4 + 1 1/4 = 3 3/4 aquí me di cuenta que ya tenía la fracción que deseaba 3/4 pero me faltaban litros completos, porque sólo llevaba 3 y comencé ahora a sumar el recipiente de 2 litros.
Entonces 3 3/4 + 2 = 5 3/4 + 2 = 7 3/4 y ¡Listo! Llegué a la respuesta correcta comprando 3 recipientes de 1 1/4 litros y 2 recipientes de 2 litros.
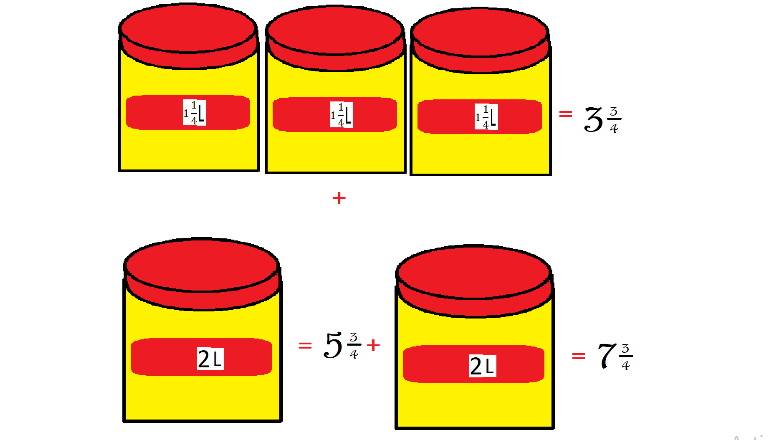
Cómo pudiste darte cuenta esa fue una interesante forma de llegar a la respuesta.
Otra forma de llegar al resultado es la siguiente.
De un compañero tuyo llamado Manuel. Él narra, así como resolvió el problema: Yo pensé en comprar 2 recipientes de 3 1/2 y sumé 1/2 + 1/2 = 1 + 3 + 3 = 7 + 1 recipiente de 1/4 y uno de 1/2 y me dio 7 3/4
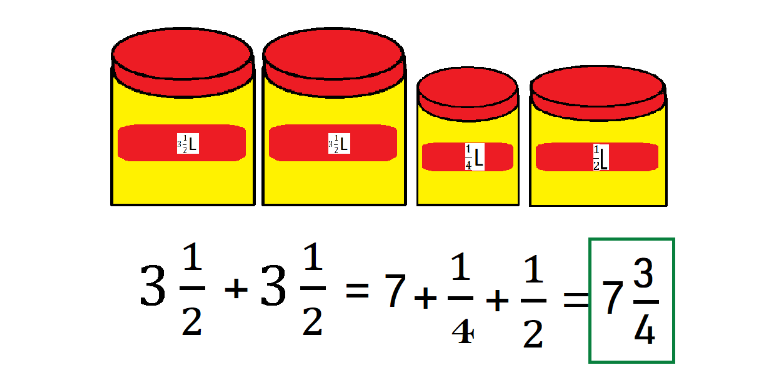
Que 1/2 es lo mismo que 2/4 y, si a eso le sumamos otro cuarto 2/4 + 1/4 = ¾ ambas respuestas son correctas igual que la de Alondra, y existen varias formas de combinar los botes de pintura que nos pueden llevar a obtener los 7 litros con 3 cuartos que necesita Luis.
Por ejemplo, si compra 15 recipientes de 1/2 litro, obtiene 7 litros y medio, más uno de 1/4 de litro, ya obtuvo lo que necesitaba; o también, 31 recipientes de 1/4 de litro, nos da como resultado 7 3/4 litros.
Eso quiere decir que hay muchas respuestas correctas, un problema puede tener varias respuestas o posibilidades como en este caso, donde tienes que juntar 7 litros con 3 cuartos y así encontrar muchas posibles combinaciones.
De esa manera se llega a la misma respuesta, pero por diferente camino.
Exacto, solo no debes perder de vista el planteamiento que pide la respuesta más conveniente, entonces por ecología y practicidad escogería la opción donde se involucre la menor cantidad de recipientes.
Se debe evitar generar basura, por lo tanto, la respuesta más adecuada es 2 recipientes de 3 1/2 litros, uno de 1/4 de litro y uno de 1/2 litro.

Eso de encontrar varios caminos a la respuesta correcta parece muy interesante y después poder analizarlas para ver cuál es lo más conveniente, de esta manera puedes comprender y entender mejor los resultados obtenidos.
Antes de despedirnos recuerda que las fracciones impropias tienen su equivalente en los números mixtos y que sustituyendo unas por otras puedes obtener resultados más rápidamente como en el caso de las pinturas, que en lugar de sumar 31 recipientes de 1/4 de litro, sumas únicamente 4 recipientes de diferentes capacidades que nos dieron el mismo resultado.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lectura






Login to join the discussion