¿Cuál tiene más volumen?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:18Aprendizaje esperado: i dentifica propiedades de los materiales.
Énfasis: i dentificar al volumen como una propiedad de los materiales al comparar distintos objetos.
¿Qué vamos a aprender?
En esta sesión continuaremos aprendiendo cómo son los materiales y otra de sus propiedades, como el volumen.
¿Qué hacemos?
Todas lo que vemos alrededor está hecho de algún tipo de material, esa es su materia y una de sus propiedades es la masa, que es la cantidad de materia que contienen los objetos. También aprendimos qué hacer para saber cuánta masa tienen las cosas, por ejemplo, utilizar una balanza, como la que hicimos en la sesión pasada.
La masa es una de las propiedades de la materia.
También quedó pendiente estudiar otra de las propiedades de la materia, de los objetos, que es el volumen. Antes de continuar quiero preguntarles, ¿Qué es el volumen? ¿Cómo se mide? ¿Qué ejemplos pueden poner del lugar donde viven que nos sirvan para identificar el volumen de los objetos?
Ya dijimos que los objetos, ocupan un lugar, que podemos distinguir un objeto de otro por su masa, me imagino que también por su tamaño, pero cómo se mide.
Con esto estamos empezando, con reconocer que, además de la cantidad de materia que tienen los objetos, todos tienen un determinado tamaño y ocupan un espacio o un lugar, esto es, tienen volumen. En esta clase nos enfocaremos en esta otra propiedad de la materia, el volumen, y en identificarlo a partir de comparar distintos objetos.
Ya empezamos diciendo que el volumen se relaciona con el tamaño de objetos, que vemos a partir de reconocer que éstas ocupan un lugar, es decir, el volumen se refiere al espacio que ocupa cada cosa u objeto. ¿Se les ocurren algunos ejemplos?
Después de entender que todos lo que nos rodea está formado por materia, podemos identificar que los distintos objetos tienen diferente tamaño, por ejemplo, si comparamos un balón de basquetbol con uno de futbol, es evidente que el de basquetbol ocupa más espacio, por lo tanto, podemos decir que tiene más volumen.
El tamaño del balón de basquetbol nos indica que tiene más volumen que el balón de futbol. En su libro de texto pueden ver esta comparación, aunque también la pueden identificar en sus casas si tienen dos balones de diferente tamaño y diferente deporte.
Esta comparación la podemos hacer a simple vista con estos objetos o con cualquier otro que tengan en casa, es decir, podemos estimar que un objeto determinado tiene más volumen que otro con el simple hecho de verlos juntos.
Creo que aquí es importante regresar a una de las preguntas que nos hiciste al principio, ¿El volumen se puede medir?
Resulta que sí, el volumen se puede medir, es decir, podemos obtener información mediante procedimientos específicos o con instrumentos especiales, con lo cual podríamos obtener información precisa acerca del volumen de los objetos. La unidad de medida del volumen, reconocida internacionalmente, es el metro cúbico, que se representa de la siguiente manera: m3.
Antes de pasar a la siguiente actividad, Te invito a leer una pequeña historia, que nos narra la manera en la que el gran Arquímedes resolvió un problema.
Arquímedes y la corona.
Érase una vez un rey y un sabio. El rey se llamaba Hierón, y el sabio, Arquímedes. Los dos vivían en Siracusa, ciudad-Estado de la Grecia Antigua. El rey mandó hacer una corona toda de oro, pero escuchó rumores de que los orfebres no habían usado oro para hacer la corona y quedó desconfiado. A simple vista la corona era totalmente dorada y se parecía mucho al oro puro, ¿cómo hacer, entonces, para estar seguro sin destruirla?
Es ahí que entra el sabio. Arquímedes ya era renombrado en aquel momento cuando el término filósofo era usado para todos los estudiosos y científicos en general y es conocido hasta hoy por sus descubrimientos en matemáticas, física y por diversas invenciones.
La historia más conocida de Arquímedes es, sin embargo, como dijimos, una leyenda. El rey consultó al filósofo para probar si la corona era toda de oro o no.
Estaba el sabio griego un buen día preparándose para tomar un baño en una bañera, entretenido con esa cuestión, cuando de repente, tuvo una visión de la solución y salió corriendo, desnudo por las calles de la ciudad, gritando “¡Eureka, Eureka!”, que en griego quiere decir “¡Lo he encontrado, lo he encontrado!”.
Así, Arquímedes descubrió mientras tomaba un baño en su tina, que la cantidad de agua que transbordaba era igual en volumen a su propio cuerpo.
Y así se dio cuenta de cómo se podría probar el fraude del orfebre. Señaló que dos bloques con la misma masa, es decir la misma cantidad de materia, uno de plata y otro de oro, elevaban diferentes niveles de agua: porque son de materiales de diferente densidad, los bloques no eran del mismo tamaño (volumen) entonces, sumergió en un recipiente lleno de agua un bloque de oro de masa igual a la de la corona y midió el volumen de agua desalojada. Hizo lo mismo con un bloque de plata. El volumen de agua desalojada por el bloque de oro era menor que el volumen de agua desalojado por el bloque de plata. Repitió la experiencia con la corona y verificó que el volumen de agua desalojada era mayor que el del bloque de oro y menor que el del bloque de plata.
Llegó a la conclusión que la corona no era de oro puro y que los orfebres la habían hecho mezclando metales. Usó este experimento para probar que la corona había sido hecha con una liga (mezcla) de oro y plata.
El rey no debe haberse quedado muy satisfecho con los orfebres.
¡Me imagino la emoción al descubrir la mejor manera de resolver un problema!
Exacto, eso hace la ciencia, observas, investigas, conoces, explicas resuelves y te emocionas.
¿Te parece si replicamos un poco el experimento de Arquímedes?
Hagamos la actividad de la página 80, de su libro de texto.

Te invito a que también, desde tu casa y con la ayuda de un familiar adulto, realicen la actividad. Para llevarla a cabo vamos a necesitar los siguientes materiales que, como verán, pueden tenerlos en casa:
- Un biberón de 240 ml o taza medidora.
- Arena.
- Semillas de frijol.
- Lo primero que vamos a hacer es poner agua en el biberón o taza medidora, de acuerdo con las marcas que tienen, podemos poner 150 ml de agua.
Tenemos una primera medida que es 150 ml de agua, ahora vamos a poner, dentro del biberón o taza medidora, cuatro cucharadas de arena y vamos a observar lo que sucede.
¿Qué es lo que pasó?
Podemos ver que el agua subió de nivel.
Además de ver el cambio de nivel, en el biberón o taza medidora tenemos una escala en mililitros (ml) y, gracias a ella, también podemos decir cuánto subió el nivel del agua. En este caso, ¿Cuánto subió?
Déjame ver, subió a 170 ml.
¡Les parece si vamos registrando los resultados?
Así no perderemos el detalle de lo que encontremos.
Ahora vamos a agregar un puñado de semillas de frijol.
¿Me pueden decir qué pasó ahora?
También subió el nivel del agua, esta vez llegó a 200 ml.
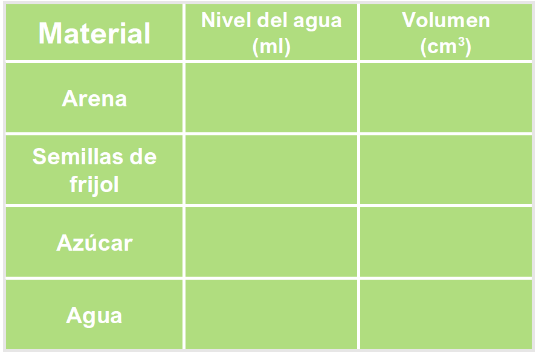
Ahora tenemos el siguiente cuadro completo con todos nuestros hallazgos, es decir, con lo que registramos después de introducir en el biberón con agua, diferentes objetos.
|
MATERIAL |
NIVEL DEL AGUA (ml) |
|
Arena |
170 ml |
|
Semillas de frijol |
200 ml |
Con esta información podemos hacernos algunas preguntas, por ejemplo, ¿Por qué subió el agua cuando le pusimos cada uno de los materiales que usamos?
Creo que el agua subió porque cada material la empujó hacia arriba.
La cantidad de arena utilizada, no pueden ocupar el mismo lugar al mismo tiempo. Por eso cuando pusimos cada material el agua se desplazó en una cantidad igual al volumen de cada material.
Entonces podemos decir que el volumen del puñado de semillas de frijol usado es de 50 ml. Porque entiendo que tenemos que ver la cantidad de agua que teníamos al principio de la actividad en el biberón y la cantidad de agua que subió cuando agregamos cada material que, en el caso de las semillas de frijol, fue de 200 ml, e decir, desplazó 50 ml de agua.
La unidad de medida del volumen, reconocida internacionalmente, es el metro cúbico, pero esta unidad resulta muy grande cuando queremos medir el volumen de líquidos o materiales que usamos diariamente. En este caso, es mejor usar una unidad mejor, el decímetro cúbico. Dado que hemos obtenido el volumen en ml, necesitamos hacerlo equivalente en decímetros cúbicos.


¿Qué nos dicen estas equivalencias?
Que un decímetro cubico ocupa el mismo espacio que un litro, que es una unidad utilizada comúnmente para medir la capacidad de los recipientes. También, nos dice que un centímetro cúbico es igual a un mililitro (ml), de manera que, si regresamos a nuestra tabla, podemos decir que el volumen calculado de, por ejemplo, las semillas de frijol que utilizamos, es de 50 cm 3 .
Entonces completemos la tabla, yo anoto.
Esta es la forma correcta de expresar el volumen de los objetos, dado que la unidad de medida del volumen es el metro cúbico (m 3 ), lo que hemos utilizado aquí es una equivalencia porque medimos el volumen de objetos pequeños.
Entonces, el volumen de la arena que usamos en la actividad es de 20 cm 3 , el de las semillas de frijol fue de 50 cm 3 .
Estos procedimientos para calcular el volumen de los objetos, nos puede ayudar a tomar diferentes decisiones, por ejemplo, cuando preparamos una receta para cocinar un postre que nos gusta, necesitamos materiales o ingredientes en cantidades exactas.
¿Qué postre vamos a preparar?
¿Qué les parece si ponemos en práctica lo que hemos aprendido acerca de la masa y el volumen de los objetos? Recuerden que éstas son propiedades de los objetos. Con todo esto que ahora sabemos de las propiedades de la materia, les propongo que, en casa, y con la ayuda de alguno de sus familiares, consigan una receta para elaborar un pastel, un panqué, galletas o el postre de su preferencia.
Esta actividad viene en la página 85 de su libro de texto. Les recomiendo que, en la medida de lo posible, la hagan con la ayuda de un adulto. Al hacerla, recuerden tener presente la receta para elaborarla, los diferentes ingredientes o cosas que necesitarán, la importancia de agregarlos de acuerdo con las indicaciones de la receta, los recipientes e instrumentos de medida que usarán, entre otras cosas.

Recapitulando lo aprendido:
- Los objetos están hechos de materia.
- La materia tiene diferentes propiedades, como son masa y volumen.
- La masa es la cantidad de materia que tiene un cuerpo u objeto y el volumen es el espacio o lugar que ocupa.
- La unidad de medida de la masa es el kilogramo (Kg) y gramo (g); y la unidad de medida del volumen es el metro cúbico (m3) o decímetro cúbico (dm3).
- Este sistema de medida es un sistema socialmente aceptado, que todos conocemos y utilizamos en nuestras diferentes actividades de la vida diaria.
- La masa de un cuerpo no se relaciona ni con su forma ni con su tamaño, se relaciona con el tipo de material del que está hecho.
- La cantidad de masa y el espacio ocupado por un objeto son propiedades diferentes e independientes entre sí.
El reto de hoy:
Con lo aprendido los invito a que reflexionen con sus familiares sobre la importancia de los procedimientos para calcular el volumen de los objetos. Al igual que con el cálculo de la masa de un objeto con ayuda de una balanza, también podemos medir el volumen como lo hicimos en esta clase.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lectura
https://www.conaliteg.sep.gob.mx/primaria.html




Login to join the discussion