¿Cuál es el sucesor?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Aprendizaje esperado: identifica una fracción o un decimal entre dos fracciones o decimales dados. Acercamiento a la propiedad de densidad de los racionales, en contraste con los números naturales.
Énfasis: identifica algunas diferencias entre el orden de los decimales y el orden de los números naturales, a partir de la propiedad de densidad.
¿Qué vamos a aprender?
Identificarás una fracción o un decimal entre dos fracciones o decimales dados a partir de la propiedad de densidad.
¿Qué hacemos?
Realiza un repaso de las diferentes clases de números que has conocido y para lo que sirven. Sin ellos no podrías contar, pesar, medir, por ejemplo, los números naturales son necesarios para contar cosas que hay a tu alrededor, encontrarás muchos objetos que te pueden ilustrar la utilidad de los diferentes tipos de números.
Actividad 1
Observa algunos objetos que podrías contar y que están a tu alcance.


Aquí observarás los números naturales 3, 4 y 100.
¿Cómo utilizas los números decimales?
Piensa cómo utilizarías los números decimales para contar, pesar o medir cosas que están a su alrededor.
Observa el ejemplo.

Como observaste, los números decimales también los puedes encontrar a tu alrededor.
Los números decimales también están en todas partes, cuando compras algo, cuando mides o pesas algo, por ello es importante conocer un poco más sobre estos números. Y precisamente de eso trata la actividad de hoy. Abre tu libro de texto en la página 73, Desafío 36. Ten a la mano una hoja o cuaderno para realizar notas, lápiz, goma, lápices de colores y regla.
https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/73

Tendrás oportunidad de repasar y profundizar en el tema de los números naturales y decimales. El desafío se llama ¿Cuál es el sucesor?
¿Sabes cuál es el significado de la palabra “sucesor” en matemáticas?
La palabra sucesor significa “el que sigue o el siguiente”.
El sucesor de un número es aquel que le sigue inmediatamente; es decir, que entre un determinado número y su sucesor, no hay otro número.
Actividad 3
Realiza las actividades siguientes:
- Representa en una recta numérica los números naturales indicados e identifica entre ellos un tercer número natural.

¿Qué tipos de números son los que presenta la actividad?
Son números naturales.
En tu libro hay una recta para localizar los números del inciso A y otra para los del inciso B. ¿Cómo colocarías los números en cada una? Escríbelos en tu libro como elijas. Si te es posible utiliza lápices de color para que puedas distinguirlos mejor.
¿Cómo se puede ubicar el 6 y el 8 en la primera recta y el 4 y 5 en la segunda?


En una numeración primero va el 6 y luego el 8, y el 4 va antes que el 5.
Como te darás cuenta, debes basarte en el orden de los números.
Ahora, ¿Cómo localizas un tercer número natural entre ellos?
Considerando la ubicación de los números que identificaste, coloca en cada recta un tercer número natural que estará entre los dos que ya pusiste; puedes hacerlo ahora con un color diferente.
Como entre el 6 y el 8, en una numeración de uno en uno, está el 7, entonces colócalo en medio y a la misma distancia del 6 y del 8.
Considerando el orden de los números, quedarían 6, 7, 8.
En la segunda recta, ¿Puedes aplicar lo mismo que en la primera? ¿Puedes localizar un número natural entre el 4 y el 5?

Como te darás cuenta, no hay números naturales entre el 4 y el 5. Aquí no podemos aplicar el mismo criterio. ¿Qué podemos hacer entonces para encontrar un número entre el 4 y el 5? ¿Hay números entre 4 y 5? ¿Qué números podemos localizar entre el 4 y el 5?
Observas la recta e intenta responder estas preguntas.
Para identificar algunos números entre el 4 y el 5 toma tu regla. En la regla localiza el 4 y el 5 ¿Ya lo tienes?

Aquí está el 4 y 5.
Observa el espacio entre el 4 y el 5 ¿Qué observas? ¿Qué hay entre el 4 y el 5 en la regla que tienes?
¿Identificaste que hay unas rayitas pequeñas que se llaman milímetros?
En la regla encontramos centímetros y milímetros. Los milímetros son pequeñas divisiones que se hacen entre un número y su consecutivo. ¿Hay números en medio del 4 y el 5?
Sí los hay, hay números pero no son números enteros, son números decimales.
Entre los números naturales están los números decimales. Para que se observes con mayor claridad, aquí tenemos una ampliación del espacio que hay entre el 4 y el 5, observa.

Aquí tienes el 4 y acá está el 5. En medio están las rayitas, son 9 rayitas y cada una representa una parte de un natural, es decir: un número decimal. Si comienzas en el 4, al avanzar hacia la siguiente rayita, ¿En qué número estarás?
Estarás en el cuatro, más un décimo, porque el espacio que hay entre el 4 y el 5 lo dividimos en diez partes.
Por eso se escribe. 4.1 el punto decimal separa la parte entera de la parte decimal.
Entonces en medio del 4 y el 5 encontramos varios números decimales.
Son: 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8 y 4.9. Todos esos números están entre el 4 y el 5.
Vuelve a la página 73 de tu libro de texto y responde, ¿Cuál es la respuesta del inciso b?
Que entre 4 y 5 no hay números naturales.

Revisa qué indicaciones tiene la actividad 2.
Representa en una recta numérica los números decimales indicados e identifica entre ellos un tercer número decimal. Ahora localiza específicamente números decimales. Tienes que encontrar un tercer número entre los que se muestran. En el inciso a están 1.2 y 1.3

¿Qué se te ocurre hacer para encontrar más números decimales?
Buscar la respuesta como se hizo en la actividad anterior.
Es como agrandar el espacio entre 1.2 y 1.3
A primera vista el 1.2 y el 1.3 pareciera que están “pegados”, es decir que ya no hay más números en medio, pero si ampliamos el espacio que hay entre ellos, descubrirás nuevos números decimales.
Se encuentran estos números: 1.21, 1.22, 1.23, 1.24, 1.25, 1.26, 1.27, 1.28 y 1.29.

Compara tu respuesta y regístrala en el espacio correspondiente, en tu libro de texto.
Resuelve el inciso b, usando el procedimiento anterior, en tu libro de texto.

Aquí se tiene el 1.23 y el 1.24 y al ampliar el espacio entre ellos, encontramos más números decimales.

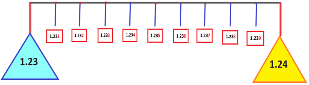
Entonces, ¿Qué números se pueden encontrar entre 87.66 y 87.67?

¿Habrá algún número entre ellos?¿Cuál será? podrías imaginar que ponemos el 87.66 arriba y el 87.67 abajo en este cuadro. Para que lo puedas enteder, si se aumenta el espacio entre ellos, ¿Qué puedes encontrar?

Vas a encontrar los números que estaban escondidos ahí en medio.
Los números que ahora ubicaste en medio de las cantidades, ¡ocupan tres posiciones después del punto!
Pero, ¿Se vale que los números decimales siempre se sigan dividiendo?
Sí, cada vez serán pedazos más chiquitos y luego otros más chiquitos y así hasta el infinito. Siempre se podrá dividir el espacio que hay entre dos números decimales, en otros más pequeños, y luego, el que hay entre éstos, en otros más pequeños y así, hasta el infinito, esas partes cada vez serán más y más pequeñas.
Recuerda que en varios momentos de la sesión has ampliado con nuestra imaginación el espacio entre dos números, para saber si entre ellos existen otros números parecidos a ellos. Ya observaste que entre dos naturales consecutivos, no se puede encontrar otro número natural, pero ten presente que con los números decimales, puedes encontrar siempre muchos más números decimales entre ellos.
Observa cómo se insertaron los decimales entre los números que había al principio de la sesión.
Primero con los números entre 4 y 5. Escribe en tu cuaderno.
Este ejercicio te dio la oportunidad de descubrir que entre dos naturales hay otros números que son distintos de los números naturales y se llaman decimales.

Después analizaste los números que había entre dos números decimales, entre 1.2 y 1.3

Y por último, analizaste los números que hay entre otros dos números decimales (1.23 y 1.24)
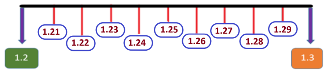
Todo lo anterior te permitió darte cuenta de que entre dos números naturales no hay otro número natural, pero que entre dos números decimales, siempre habrá otros muchos números decimales.
¿A qué conclusiones puedes llegar en esta sesión?
- La primera es que entre dos números naturales consecutivos, no existe otro número natural.
- La segunda es que entre cualquier par de números decimales, siempre podrás encontrar muchísimos números decimales. Los números son infinitos.
El reto de hoy:
Comparte con alguien cercano lo que aprendiste hoy, utilizando tu regla, explícale cuáles son los numeros naturales y como entre estos hay otros llamados números decimales y, como entre estos, puede haber muchos más.
Si te es posible, consulta otros libros y comparte el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion