¿Cuál es el bueno?

¿Cuál es el bueno?

Aprendizaje esperado: anticipación y comprobación de configuraciones geométricas que permiten construir un cuerpo geométrico.

Énfasis: utilizar la imaginación espacial para identificar y completar desarrollos planos que puedan dar origen a un cuerpo geométrico determinado.

¿Qué vamos a aprender?

Aprenderas a usar la anticipación y comprobación de configuraciones geométricas que permiten construir un cuerpo geométrico, así también vas a utilizar tu imaginación espacial para identificar y completar desarrollos planos que puedan dar origen a un cuerpo geométrico determinado.

¿Qué hacemos?

Recuerda que para esta sesión debiste preparar con anticipación el material siguiente:

• El primer material es un cuadrado de 12 cm por lado que está dividido en 9 cuadraditos iguales que miden 4 cm por lado.
• Y el segundo, es una tira compuesta por nueve cuadraditos de 4 cm de lado cada uno.
• El cuadrado tiene marcado unas líneas punteadas que indican dónde lo vamos a recortar.

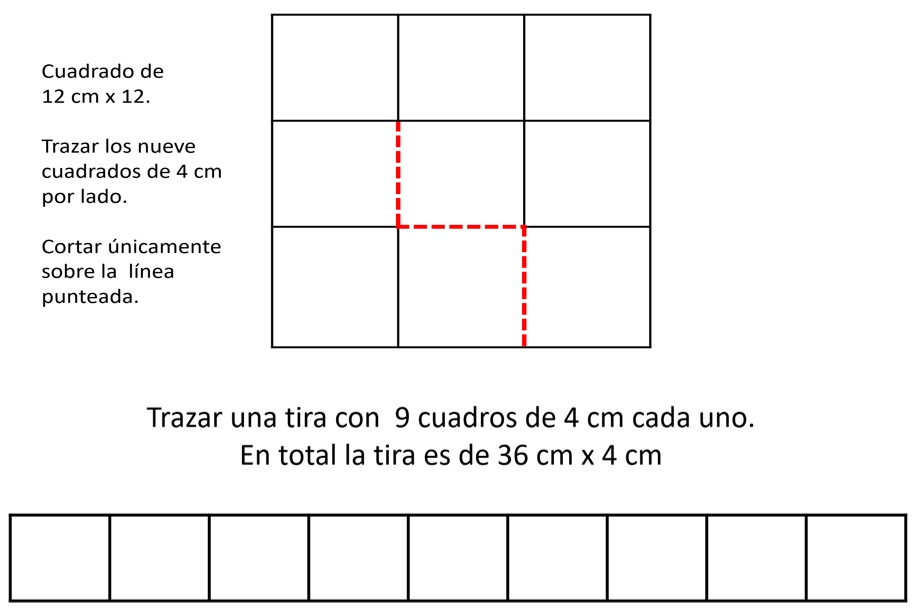
Este material lo debes tener listo al igual que tu libro de Desafíos matemáticos, un cuaderno u hoja para tomar notas, lápiz, goma y sacapuntas.

https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/123

También vas a emplear la imaginación espacial que es la habilidad de visualizar en tu mente los trazos, las formas y las transformaciones geométricas de figuras o cuerpos sin tener que dibujarlos, o bien, antes de hacerlo, un ejemplo, es la actividad que plantea el desafío que trabajaste al adivinar cuál es el cuerpo oculto.

Recuerda que anteriormente también hubo una sesión relacionada con volumen, donde se dio un ejemplo, cuando debías imaginar si un mueble, como un sillón, pasaba por una puerta, sin tener que medirlo o traerlo para comprobarlo.

Hoy nuevamente pondrás en práctica la imaginación espacial. La utilizarás para aplicar algunos conceptos que ya se has trabajado en otras sesiones.

Ahora toma tus materiales y elige con cual de los que preparaste quieres empezar, ya sea el cuadrado o la tira cuadriculada, con cualquiera de los dos vas a formar un cubo.

Te preguntarás si con la tira se puede formar un cubo.

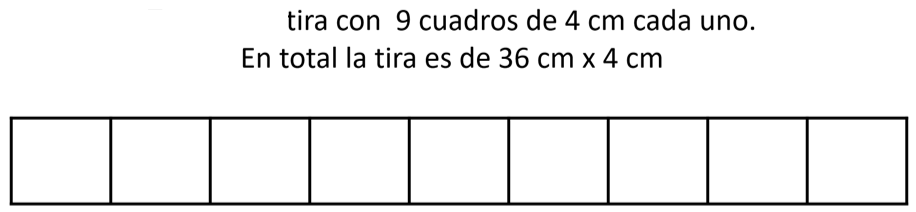
Recuerda usar tu imaginación. Imagina cómo es el cubo, ¿Recuerdas algunas de sus características? Son las siguientes:

• Cuerpo geométrico.
• ¿Es un prisma o pirámide? Es un prisma.
• ¿Cuántas caras tiene y de qué forma son? Tiene cuatro caras y dos bases. Pero sus caras y bases tienen la misma forma y el mismo tamaño. El cubo es un caso especial de prisma pues todas sus caras son iguales, entonces tiene caras laterales y bases iguales, está formado por seis cuadrados iguales.
• Si todas las caras son iguales, tanto laterales como las de la base, las aristas también son iguales y tiene doce.

Trabaja con la tira o con el cuadrado para formar un cubo, o bien, decide con cuál trabajar. Recuerda que la única condición es que en el cuadrado solamente están recortadas las líneas punteadas con rojo.

Para construirlo debes usar la imaginación, ya tienes los cuadraditos del mismo tamaño que forman tanto las bases como las caras laterales, también sabes que un cuerpo geométrico tiene tres dimensiones: largo, ancho y altura.

Es cuestión de imaginar qué puedes hacer con los cuadritos que sobran, porque un cubo tiene dos bases y 4 caras laterales. En total, son 6 cuadrados los que forman todas sus caras.

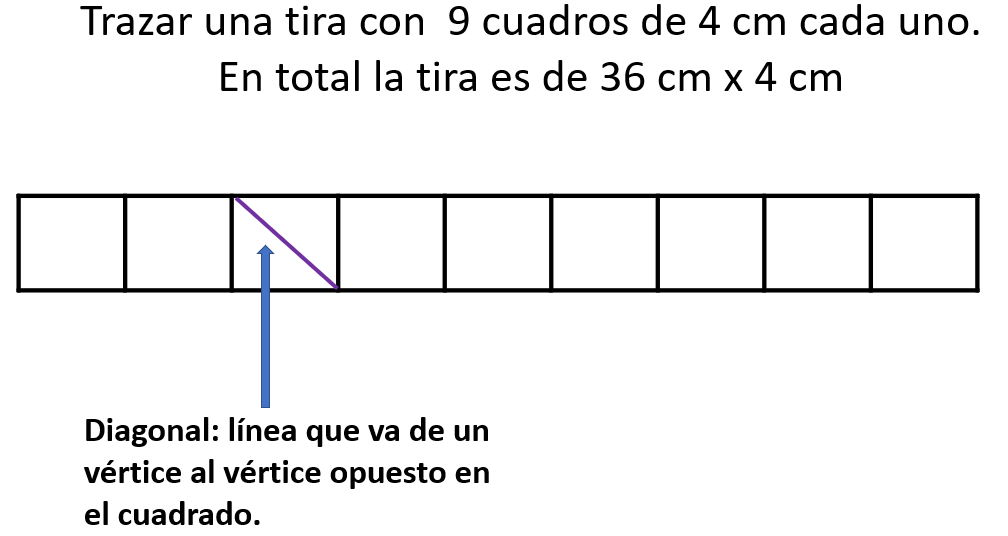
Para armarlo observa bien qué sucede con los cuadraditos que la tira tiene de más. Al armarlos tienen un doblez en diagonal, es decir, se hace un doblez a partir de un vértice a un vértice opuesto a él. Con los dobleces en diagonal se puede manipular la tira o el cuadrado para llegar a formar un cubo.

Recuerda que la única regla es no recortar el material y si utilizar la imaginación, así puedes llegar a armar el cubo con algunos dobleces que ocultan los cuadraditos que sobran.

Poco a poco irás aprendiendo a observar y a aplicar lo que ya conoces de los cuerpos geométricos, recuerda utilizar la información que te proporcionan y visualizar en tu mente lo que te solicitan, buscando estrategias diferentes de resolverlo.

Ahora, es momento de utilizar tu imaginación con lo que te plantea el libro. Ve al Desafío 65 página 123 de tu libro de texto, ¿Cuál es el bueno?

La consigna dice lo siguiente:

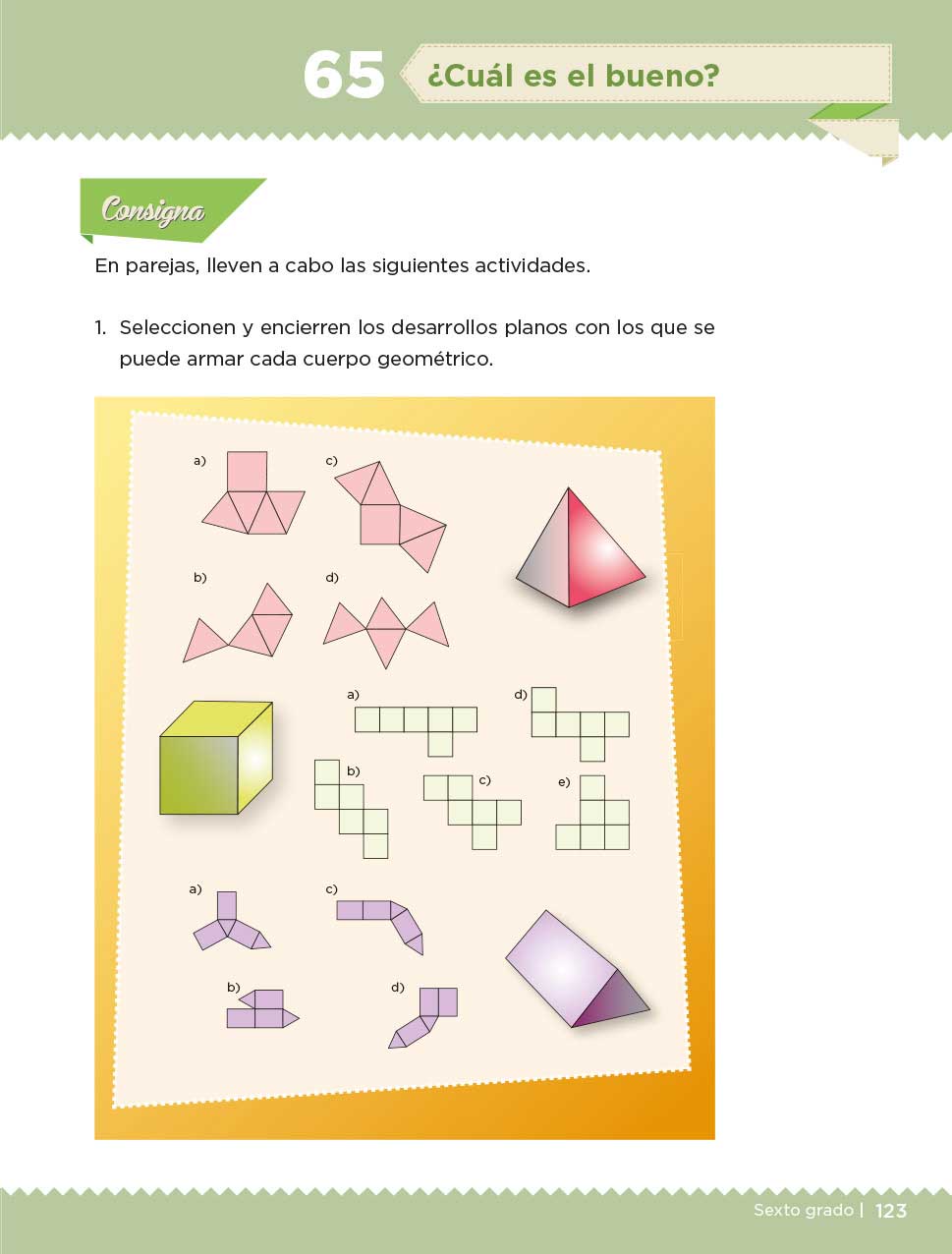
En parejas, lleven a cabo las siguientes actividades. Actividad 1. Seleccionen y encierren los desarrollos planos con lo que se puede armar cada cuerpo geométrico.

Para empezar, ¿Recuerdas qué es un desarrollo plano? Por lo que observas en tu libro es como el cuerpo geométrico extendido, desdoblado. El desarrollo plano es el trazo de cada una de las figuras geométricas que forman el cuerpo, bases y caras laterales, organizadas de tal manera que, al realizar los dobleces sobre algunas aristas, se forma el cuerpo geométrico.

Como en la actividad anterior, pero aquí no te sobran ni bases ni caras laterales y los dobleces forman las aristas del prisma o pirámide a formar.

En la imagen que aparece en tu libro, hay tres cuerpos geométricos, uno color rosa, uno verde y uno morado. ¿Ya identificaste cuáles son los cuerpos geométricos en la imagen?

https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/123

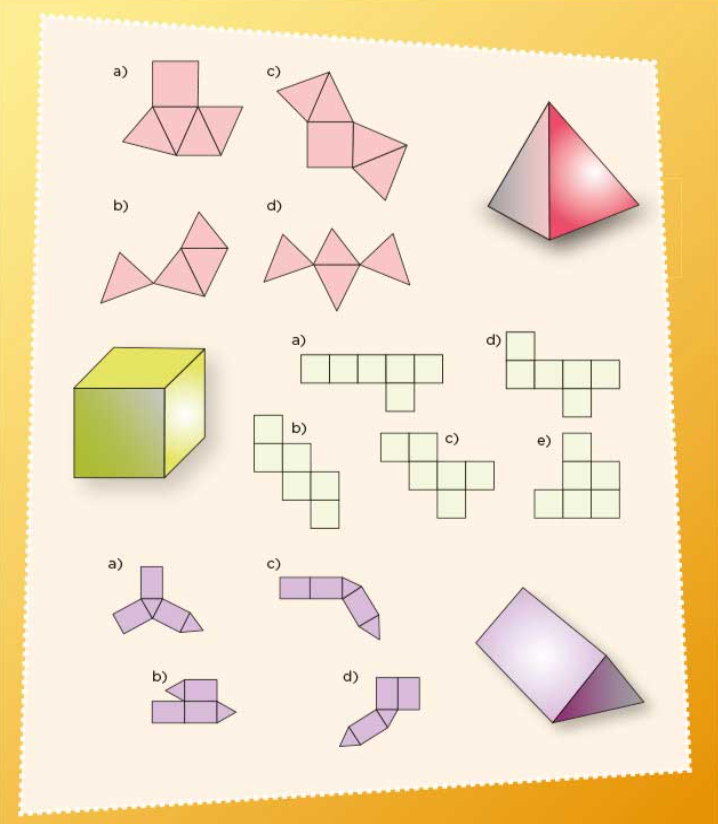
En la imagen del lado derecho está el cuerpo geométrico rosa. Abajo, del lado izquierdo está el verde y sigue el morado.

Ahora observa cuidadosamente, usa tu imaginación, y en tu mente ve ideando cómo se vería cada vez que haces un doblez sobre cada línea, en qué posición quedaría la cara del cuerpo, para que puedas elegir con cuál de los desarrollos planos podrías formar el cuerpo geométrico que está dibujado ahí.

Empieza uno por uno. ¿Cuál cuerpo geométrico es el primero que tienes que imaginar para encontrar su desarrollo plano? Es una pirámide. Ahora, ¿Cuál es el polígono que sirve de base en la pirámide? Un triángulo.

Puede ser un triángulo, pero observa bien las aristas de la pirámide, y compara con los lados de los triángulos, ¿Qué posición tienen y si es posible armar la pirámide o no? Lo notas, más bien es una pirámide triangular, porque se nota que en las aristas de la base se forma una L es decir, un ángulo recto o de 90 grados.

Observa detenidamente la imagen e imagina que es una pirámide triangular. Tendrías que imaginar que en la base sólo falta por ver una arista y estaría completo el cuerpo geométrico.

Ya observaste una imagen, de acuerdo con tus conocimientos sobre los cuerpos geométricos. Ahora imagina que tienes otro polígono de base, como un cuadrado. ¿Qué tendrías que imaginar? Pues si fuera cuadrada la base, entonces faltan dos aristas del polígono en la base y una que va del vértice que se forma con estas dos aristas y que no estas viendo hacia arriba.

De acuerdo con lo que imaginaste y observaste en las imágenes, ya puedes asegurar cuál es el polígono de la base. Observa con detenimiento los desarrollos planos que tienes a un lado del cuerpo geométrico e imagina como doblarlos, en este caso sería sobre las aristas para buscar cuál corresponde con la base que identificaste, así podrías saber cuál es el desarrollo plano que buscas.

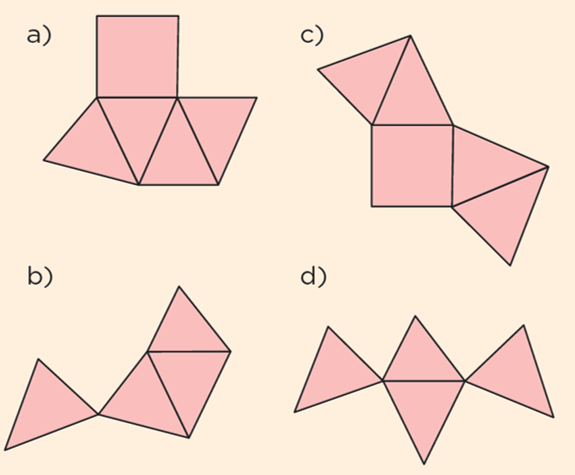
Con base en este ejercicio, en una hoja, calca los desarrollos planos y trata de formar el cuerpo geométrico, te quedará muy pequeño, pero te permitirá acercarte a la respuesta, entonces, podrás comprobar que es una pirámide cuadrangular.

Ahora busca, imagina y comprueba cuál es el desarrollo plano que te permite armar completamente el cubo y el prisma triangular.

https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/124

Poco a poco se te irá facilitando identificar el desarrollo plano de un cuerpo geométrico, es decir, imaginar si al recortarlo y construirlo se obtiene lo que se había pensado.

Recuerda que, para ello debes tomar en cuenta sus características, la forma de su base y de sus caras laterales, ya sea que se trate de un prisma o de una pirámide.

Al visualizar los objetos geométricos y aplicar los conocimientos que has adquirido, poco a poco puedes descubrir el desarrollo plano correcto usando tu imaginación espacial, aunque si tienes dudas es válido recurrir a estrategias para comprobar si estás en lo correcto, cómo recortar los desarrollos planos y comprobarlos. Como en este caso, donde realizaste la actividad uno, y comprobaste recortando y haciendo los dobleces necesarios en los desarrollos planos que te presenta el libro, de esta manera lograrás estar seguro de la respuesta.

El reto de hoy:

Completa lo que te propone el desafío y coméntalo con alguno de tus familiares, seguro le parecerá muy interesante y atractivo.

Si te es posible, consulta otros libros o materiales para saber más sobre el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.