¿Con la magnitud de la masa podemos contar?

¿Con la magnitud de la masa podemos contar?

Aprendizaje esperado: relaciona la masa de las sustancias con el mol para determinar la cantidad de sustancia.

Énfasis: relacionar masas y masas atómicas para calcular la cantidad de sustancia con su respectiva unidad de medida.

¿Qué vamos a aprender?

Lee la siguiente frase del físico austriaco Erwin Schrödinger:

“La vida parece ser el comportamiento ordenado y reglamentado de la materia basado en parte en mantener el orden existente.”

En esta sesión reflexionarás sobre la definición y el origen de una de las siete magnitudes fundamentales en el Sistema Internacional de Unidades: el mol.

También sobre los cambios que ha tenido su definición y la relación con el número de Avogadro, revisado en la sesión anterior.

Finalmente, sobre su importancia y uso en la química, pues te permitirá establecer la proporción entre los reactivos y productos en una reacción química.

Registra las dudas, inquietudes o dificultades que te surjan al resolver los planteamientos de esta sesión.

Puedes resolver los cuestionamientos con respecto al tema de cantidad de sustancia al revisar los ejemplos que aparecen en tu libro de texto, al reflexionar en torno a los problemas que se te presentarán y al resolver la actividad planteada en la sesión, además, puedes consultarlas con tu maestra o maestro de la asignatura de Ciencias Química.

¿Sabías qué? El 16 de noviembre de 2018, metrólogos de todo el mundo se reunieron en la Cámara del Congreso del Palacio de Versalles, para redefinir cuatro unidades fundamentales del Sistema Internacional (SI): el amperio, el kelvin, el kilogramo y el mol. Estas unidades, como el metro, la candela, y el segundo, dejaron de tener un patrón tangible y pasaron a definirse en relación con constantes físicas fundamentales.

Las unidades adoptaron su nueva definición el 20 de mayo de 2019, el Día Mundial de la Metrología. Aunque la mayoría de las personas que no están familiarizadas con las ciencias, no notaron el cambio, era necesario el aumento en la precisión de las medidas pues las tecnologías de medición han avanzado tanto que han permitido detectar márgenes de errores cada vez más pequeños.

Te imaginas haber tenido que medir en pies, brazos, codos, piedras o pulgares, todos son de tamaños diferentes.

La Academia de Ciencias, instituida después de la revolución francesa, busco estandarizar la forma en que se medía el mundo. Utilizaron unidades que consideraron ser universales y no cambiaran de persona a persona, como la distancia del ecuador al polo norte, o una pesa conformada de una aleación de platino e iridio, que pensaron la volvería resistente a la oxidación y por lo tanto perduraría para todas las generaciones, y así lograría su cometido de que todas las medidas fueran para todas las personas para siempre.

Después cuando el sistema métrico se volvió estándar por la conquista de Napoleón en Europa, se mandaron hacer réplicas del kilogramo original localizado en Francia para los demás territorios, pero con el paso del tiempo todas variaron en peso. Todos los kilogramos modelo pesaban distinto y de ahí la necesidad de crear una unidad de medida definida por algo constante como: La constante de Planck.

El mol, la medida utilizada para calcular la cantidad de átomos en una sustancia y que originalmente se definió como la cantidad de átomos en 32 g de oxígeno estaba destinado a ser redefinido, por ende.

Y así es como, a partir de mayo de 2019, el kilogramo se definió con relación a la constante de Planck, y el mol a su relación con el kilogramo.

Los materiales que utilizarás en esta sesión es tu libro de texto de Ciencias con énfasis en química, tu cuaderno de notas y tu tabla periódica.

¿Qué hacemos?

El modelo analógico o uso de analogías te puede ayudar en esta construcción, ya que favorece la visualización de los conceptos científicos, que en la mayoría de los casos son abstractos. Las analogías te ayudan a modelizar estos conceptos y a entenderlos mejor.

En este caso se te recomienda la analogía de los granos de trigo y el tablero de ajedrez, que puede ser muy útil para que dimensiones las cantidades tan grandes con las que vas a tratar. Puedes encontrar esa analogía en la siguiente dirección electrónica.

https://matematicascercanas.com/2014/03/10/la-leyenda-del-tablero-de-ajedrez-y-los-granos-de-trigo/

Seguramente en la cocina habrás notado el recipiente donde se guarda la sal, el azúcar o los granos de arroz, pero te has preguntado alguna vez: ¿Cuántos pequeños cristales de sal o de azúcar contiene ese recipiente? ¿Cuántos granos de arroz se encuentran dentro?

Seguramente te imaginaste un número muy grande.

¿De qué utilidad es conocer ese número?

Es más sencillo, utilizar la unidad de masa y colocar un kilogramo en una bolsa sin tomar en cuenta el número de cristales de sal que contiene.

Imagina un solo grano de arroz, que tiene una masa de 0.00002 kg, eso quiere decir que en un solo kilogramo de arroz tenemos 50,000 granos.

En tu vida cotidiana no tiene mucha utilidad saber ese número exacto, pues al cocinarlo no se cuenta cada grano.

¿Qué sucede en la química cuando hablas de átomos de diferentes elementos y de cómo reaccionan entre ellos para formar moléculas? En ese caso cada átomo cuenta y por lo tanto es necesario conocer de una manera precisa el número de átomos, moléculas o iones que intervienen.

Los químicos se dieron a la tarea de establecer un número que permita conocer la cantidad de átomos, moléculas, iones o cualquier otra partícula determinada, presentes en un volumen de gas a temperatura y presión constantes.

El principal de ellos fue Amadeo Avogadro, por eso esta constante lleva su nombre.

Y te indica el número de átomos, moléculas o partículas constituyentes que se encuentran en un mol de cualquier sustancia.

Para comprender mejor el trabajo de Amadeo Avogadro y la relación entre la presión, el volumen y la temperatura de un gas, observa con atención el siguiente video.

1. Video Anexo 2

https://youtu.be/YAiu-m_8ouc

(del min. 9.00 al 12.45)

En 1971 se incluyó en el Sistema Internacional de Unidades una nueva magnitud fundamental, el mol.

Hasta hace poco se definía como la cantidad de materia que hay en tantas partículas elementales como átomos hay en 0.012 Kg del isotopo de carbono 12.

A partir del 20 de mayo del 2019 el mol es la cantidad de entidades, desde electrones hasta moléculas, equivalente al número de Avogadro.

6.022 x1023

El 23 de octubre se celebra el Día Mundial del Mol, una jornada en la que se pretende despertar el interés de la población por la química, una de las ciencias más prácticas e importantes.

Se celebra entre las 6.02 am y las 6.02 pm del mes 10 el día 23 o sea 6.02 X10 a la 23, el número de “partículas” que hay en un mol, es decir, es el número de Avogadro: el número de partículas que hay en un mol de cualquier sustancia o especie química, sean moléculas, iones o partículas subatómicas.

Ahora, para utilizar las aportaciones de Avogadro y su constante, recuerda los valores que aparecen en la tabla periódica.

Cada elemento tiene su masa atómica, que, si lo expresas en kilogramos corresponde a su masa molar, es decir, la masa por unidad de cantidad de sustancia y se expresa en kilogramos/mol, aunque es más común expresarlos en gramos/mol.

Para el Hidrógeno su masa atómica es aproximadamente 1, redondea estos valores para facilitar los cálculos, entonces su masa molar será de 1g/mol. Sin embargo, el hidrógeno en el medio ambiente se encuentra como molécula diatómica H2, por lo que su masa molar será de 2g/mol que contienen 6.022 x1023 moléculas de este gas.

Para el Helio su masa atómica es aproximadamente 4, entonces su masa molar será de 4 g/mol y estos 4 gramos de Helio contendrán 6.022 x1023 átomos de este gas.

Por último, el Litio, su masa atómica es aproximadamente 7, entonces su masa molar será de 7 g/mol y estos 7 gramos de Litio contienen 6.022 x1023 átomos de este elemento.

Y así se puede continuar con los 118 elementos de la tabla periódica.

Para que sea aún más claro este concepto, observa el siguiente ejemplo utilizando diferentes semillas.

Utilizarás 200 granos de arroz y los colocarás sobre la balanza, registra la masa, que es de 8 gramos.

Enseguida toma 200 lentejas y las colocas del mismo modo sobre la balanza, registra la masa que es de 10 gramos.

Finalmente, toma 200 semillas de frijol y las colocas sobre la balanza, registra su masa que es de 20 gramos.

Del mismo modo que ocurre con los elementos, la masa de cada grupo de 200 semillas es diferente pero la cantidad de estas es exactamente la misma.

¿Qué sucedería si no fueran elementos?

Si son compuestos químicos formados por 2 o más elementos.

¿Cómo calcularías su masa total?

Recuerda que en este caso se habla de la masa molecular por tratarse de un compuesto.

Tendrías que seguir este procedimiento.

Ahora, utiliza 2 compuestos sencillos.

Primero el agua:

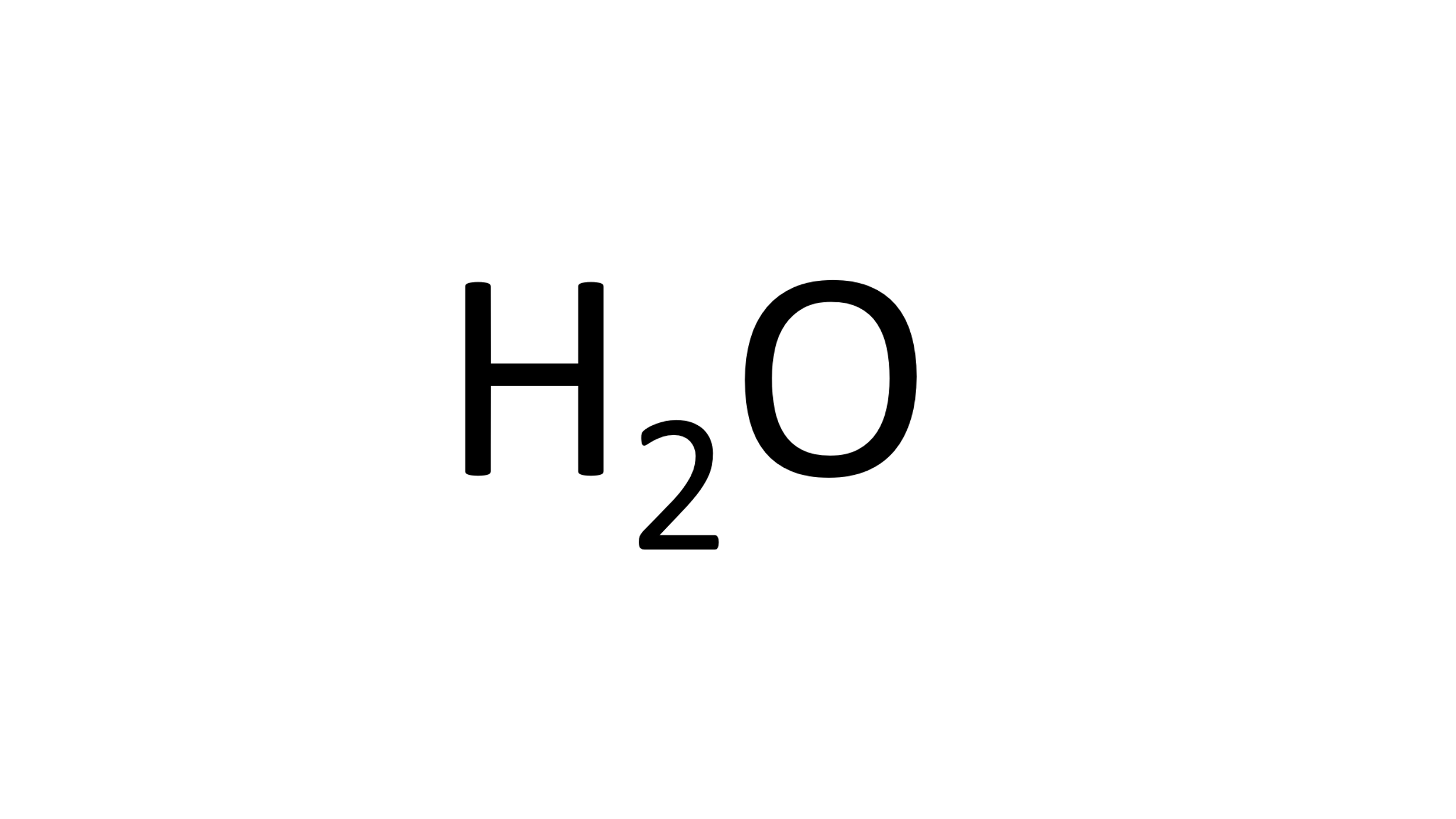
Identifica su fórmula química y los elementos que la componen.

Enseguida observa la cantidad de átomos de cada elemento que participa.

Con la ayuda de la tabla periódica identifica la masa atómica de cada elemento, que expresada en g/mol es la masa molar, 1 g/mol para el Hidrogeno y 16 g/mol para el oxígeno.

Realiza las operaciones necesarias como aparece en la siguiente tabla de izquierda a derecha:

El elemento Hidrógeno tiene masa molar de 1 g/mol, en la molécula del agua hay 2 átomos de hidrógeno, entonces 1x2 es igual a 2.

El Oxígeno tiene masa molar de 16 g/mol y en la molécula de agua hay 1 átomo, así que 16 x 1 es igual a 16.

Entonces, la masa molecular del agua se obtiene sumando 2 más 16, que es igual a 18 g/mol.

Ahora con el ácido sulfúrico:

Identifica su fórmula química y los elementos que lo componen.

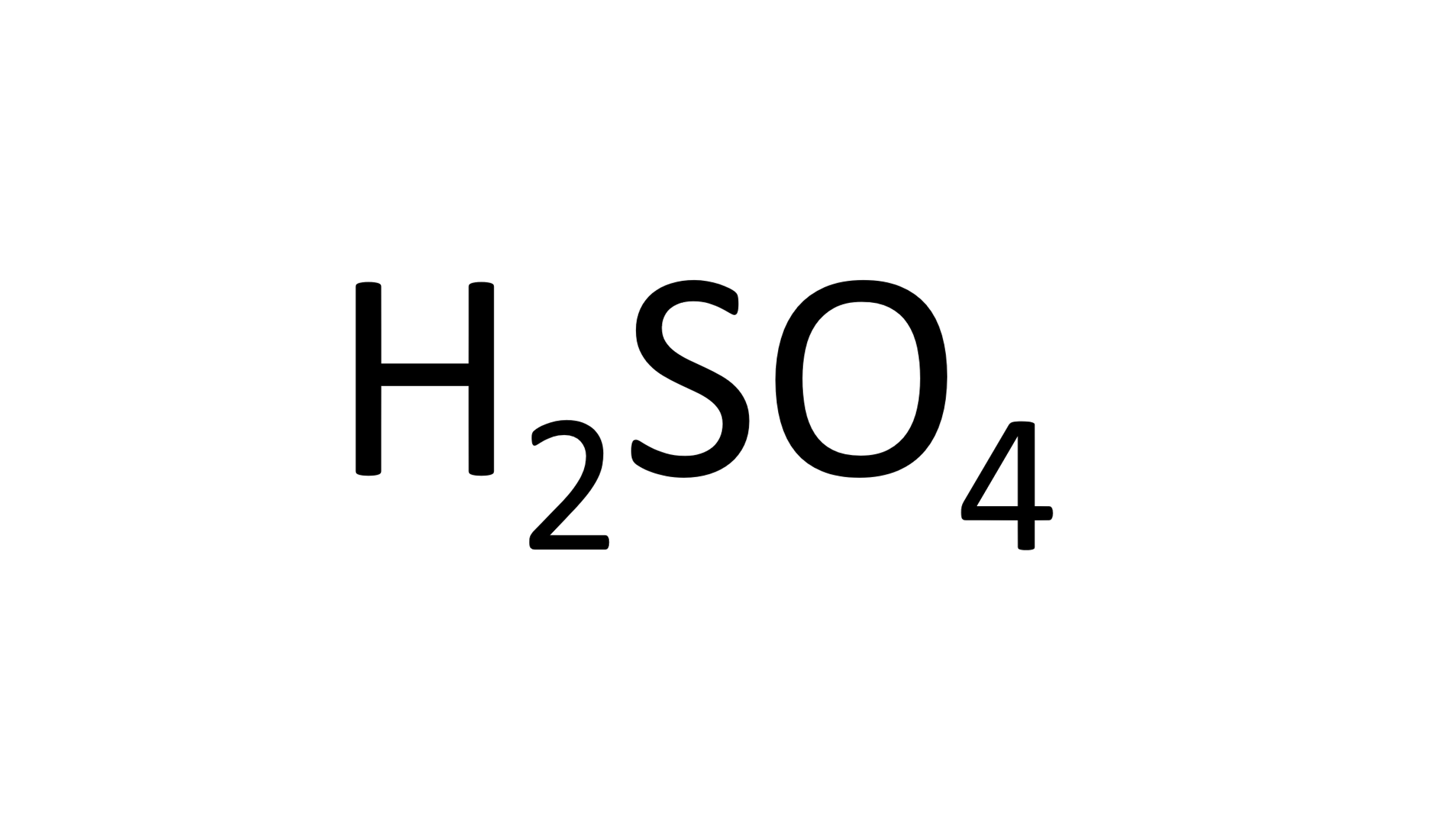
Enseguida, observa la cantidad de átomos de cada elemento que participan.

Después, con la ayuda de la tabla periódica identifica la masa atómica de cada elemento, que expresada en g/mol es la masa molar, 1 g/mol para el Hidrogeno, 32 g/mol para el azufre y 16 g/mol para el oxígeno.

Realiza las operaciones necesarias como aparece en la siguiente tabla:

Elemento Hidrógeno, masa molar 1 g/mol, átomos en la molécula 2 total 2.

Elemento Azufre, masa molar 32 g/mol, átomos en la molécula 1 total 32.

Elemento Oxígeno, masa molar 16 g/mol, átomos en la molécula 4 total del elemento, que son 64 y total del compuesto 98 g/mol.

¿Cuántas moléculas de ácido sulfúrico hay en un mol de este compuesto?

6.022 x1023

Ahora calcula la cantidad de mol presentes en un elemento o compuesto. Esto es muy sencillo, basta con dividir los gramos del elemento o compuesto entre la masa molar, que recuerdes, es la masa atómica expresada en g/mol.

Revisa el siguiente ejemplo:

¿Cuántos mol de sodio hay en 50 g de este elemento?

Para resolverlo utilizarás la siguiente relación sencilla

De este modo tienes ya la masa de la sustancia, 50 gramos de sodio, mientras que para la masa molar revisa tu tabla periódica.

Redondea el valor tienes 23 g/mol.

Realiza la sustitución de los valores y la operación.

De este modo obtienes que en 50 gramos de sodio hay 2.17 mol

Para el último ejemplo harás algo más interesante, realizarás un procedimiento similar, pero con un compuesto.

¿Cuántos mol de sal de mesa (cloruro de sodio) hay en 150 gramos de este compuesto?

Y es cuestión de repetir el proceso, primero, identifica su fórmula química y los elementos que la componen.

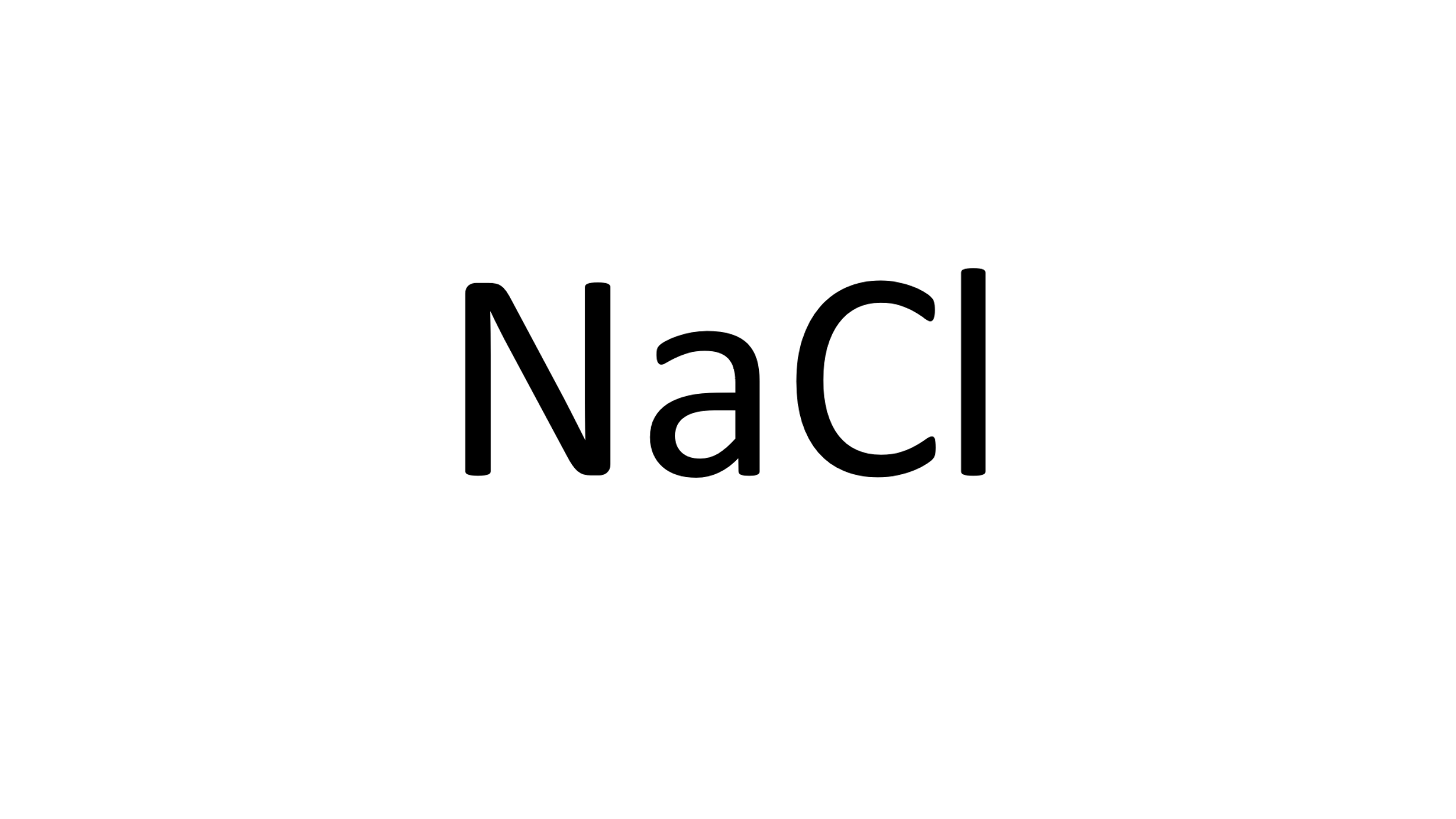
Enseguida, observa la cantidad de átomos de cada elemento que participa.

Después, con la ayuda de la tabla periódica identifica la masa atómica de cada elemento,

Que expresada en g/mol es la masa molar, 23 g/mol para el Sodio, 35 g/mol para el Cloro.

Realiza las operaciones necesarias como aparece en la siguiente tabla de izquierda a derecha:

Elemento Sodio, con masa molar igual a 23 g/mol, átomos en la molécula 1, total 23.

Elemento Cloro, con masa molar de 35 g/mol, átomos en la molécula 1, total 35.

Total, del compuesto 58g/mol.

Tienes entonces la masa molecular del cloruro de sodio que es igual a 58 g/mol, para calcular el número de moles en 150 g de sal utilizas la fórmula del ejemplo anterior.

Realizas la sustitución de los valores y la operación.

De este modo obtendrás que en 150 gramos de cloruro de sodio hay 2.58 mol.

Para finalizar, en una ecuación química los coeficientes que se colocan para cumplir con la ley de la conservación de la materia también puedes representar los moles de cierto elemento o compuesto de la siguiente forma:

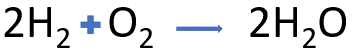
2 mol de Hidrógeno reaccionan con un mol de Oxígeno para formar 2 mol de agua.

Si utilizas las masas molares podrás saber que 4 g de hidrógeno molecular H2 reaccionan con 32 g de oxígeno molecular O2 y se forman 36 g de agua.

Si recuerdas, las proporciones de las sustancias que participan en una reacción química siempre se conservan, así que, si tuvieras 4 mol de hidrógeno reaccionarían con 2 mol de oxígeno y formarían 4 mol de agua.

¿Puedes calcular la masa de agua que se produciría en este último ejemplo?

Completa la siguiente tabla:

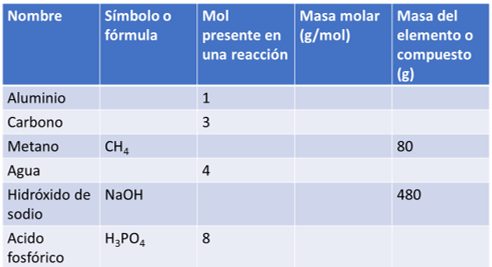
Con la masa molar, molecular y el número de mol de los elementos y compuestos que aparecen.

Asimismo, realiza el proceso anterior, considera la ecuación química, como puedes observar las proporciones siempre se conservan.

Otro uso es medir la concentración de disoluciones químicas empleando el concepto de mol. Es muy útil, pues da una idea precisa de cuántas partículas de soluto están disueltas en un cierto volumen de disolución.

En el Vademécum (libro de especialidades farmacéuticas), que es muy utilizado por los profesionales sanitarios para prescribir medicamentos, se anunciaba una versión A de un medicamento, donde cada comprimido contenía 256.30 mg de sulfato ferroso, equivalente a 80 mg de hierro. En otra versión B de ese mismo medicamento se indicaba que el contenido de dicha sal, por comprimido, es de 270 mg, también equivalente a 80 mg de hierro ¿cuál de los dos medicamentos indica la equivalencia correcta?

Una vez que analizaste os cálculos estequiométricos de los componentes del medicamento, el laboratorio de la versión B corrigió la cantidad como la versión A.

Éste es un caso de repercusiones reales que tienen las unidades de medida que utilizas. Sucedió en España, y puedes pensar, en todo caso la diferencia de valores no era elevada, pero la pregunta permanece ¿qué sucedió con los pacientes que tomaron la versión mal calculada? ¿obtuvieron el resultado esperado en su salud?

Este caso está relacionado con la medicina, pero el cálculo estequiométrico también se aplica en la elaboración de fertilizantes, aguas minerales, bebidas energéticas, productos de limpieza y belleza entre muchos otros.

El reto de hoy:

Pon en práctica tus habilidades científicas y tecnológicas, se te recomienda visitar las siguientes páginas electrónicas, en donde podrás resolver actividades prácticas relacionadas con el tema.

https://www.lamanzanadenewton.com/materiales/quimica/lmn_qui_fch12-s1.html

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/4quincena9/4q9_contenidos_3a.htm

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html