Completar el trinomio cuadrado perfecto

Completar el trinomio cuadrado perfecto

Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado

Énfasis: resolver problemas cuadráticos usando factorización.

¿Qué vamos a aprender?

En esta sesión estudiarás un caso especial de resolución de ecuaciones de segundo grado mediante el método de factorización, pero completando cuadrados.

No olvides registrar tus dudas, inquietudes y anotaciones respecto a esta lección. Podrás apoyarte en tu libro de texto para consolidar los aprendizajes.

Estudiarás ecuaciones de segundo grado que no tienen en su primer miembro trinomios cuadrados perfectos.

¿Qué hacemos?

Inicia con una situación que aparece propuesta en el libro de texto:

Luis es un profesor de tercer grado de secundaria, él les propuso a sus alumnos como un reto resolver, integrados en equipos, una situación que puede ser modelada y resuelta mediante una ecuación de segundo grado de la forma: equis cuadrada más be equis más ce igual a cero, donde a debe ser siempre diferente de cero; y en este caso a es igual a uno o bien diferente de uno, pero no es un número cuadrado.

Después de analizar la información de la situación, una de sus alumnas llamada Roxana propuso a sus compañeros de equipo que la situación se podía modelar con la ecuación: equis cuadrada menos cuatro equis más tres igual con cero, el profesor les indicó resolver la ecuación utilizando el método de factorización, con la condición de transformar el trinomio de segundo grado escrito en el primer miembro como un trinomio cuadrado perfecto; por lo que Eduardo, otro de los alumnos integrantes del equipo, les mencionó que sí era posible lograr lo que el profesor Luis les indicaba.

Mariana, otra de sus compañeras de equipo, preguntó a Eduardo: ¿y por qué afirmas eso? Eduardo les dijo: miren vamos a analizar con cuidado la ecuación propuesta por Roxana y se darán cuenta que es cierto que no se tiene un trinomio cuadrado perfecto en el primer miembro de la ecuación, cuya factorización sería un producto de binomios semejantes, o bien, expresarlo como un binomio al cuadrado.

Eduardo les dijo: recuerden que el profesor Luis ya explicó antes, que para que se tenga un trinomio cuadrado perfecto se deben cumplir tres requisitos:

El primero es que el polinomio tenga tres términos, el segundo es que dos de los términos sean cuadrados, y el tercero es que el tercer término sea igual al doble del producto de las raíces de los dos términos cuadrados.

Observemos que en la ecuación: equis cuadrada menos cuatro equis más tres igual a cero, se tiene en el primer miembro, un término cuadrático “a equis cuadrada”, al cual se le puede extraer la raíz cuadrada; un término lineal o de primer grado, “be equis”; y un término numérico, “ce”, por lo que no se puede factorizar como un trinomio cuadrado perfecto debido a que no está completo.

¿Cómo explicó Eduardo a sus compañeros la manera en que se puede proceder para completar un trinomio y que sea cuadrado perfecto?

Eduardo les dijo: ¡en realidad, compañeros, el procedimiento es muy sencillo! pongan mucha atención, se requieren realizar algunas operaciones vinculadas con los términos algebraicos, es decir, con el término cuadrático y con el término lineal o de primer grado, veamos cómo:

Para completar el trinomio: equis cuadrada menos cuatro equis más tres, en la ecuación donde el segundo miembro es cero, operaremos con el binomio equis cuadrada menos cuatro equis, lo escribimos en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego más tres igual a cero.

Obtenemos la mitad del coeficiente del término de primer grado: cuatro entre dos es igual a dos, dicho valor ahora se eleva al cuadrado y el valor obtenido se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumamos cuatro también restamos cuatro, lo que significa que hemos sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos cuatro equis más cuatro menos cuatro más tres igual a cero.

¿Pudiste descubrir el trinomio cuadrado perfecto? La respuesta es equis cuadrada menos cuatro equis más cuatro. Y además es equivalente a tener un binomio al cuadrado.

Recuerda que se identifican los dos términos cuadrados del trinomio y le extraes la raíz cuadrada, preparas un paréntesis en el cual a continuación anotas las raíces separadas del signo que tenga el otro término que es equivalente con el doble del producto de las dos raíces obtenidas, sólo falta agregar el exponente dos al binomio.

En este caso el trinomio equis cuadrada menos cuatro más cuatro es equivalente con el binomio equis más dos al cuadrado.

Después de tener el binomio al cuadrado ahora escribe menos cuatro más tres igual a cero.

A continuación, se reducen los términos numéricos, quedando el binomio equis más dos al cuadrado menos uno igual a cero.

A partir de aquí, puedes continuar resolviendo la ecuación recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación para determinar los valores de las raíces de equis.

Recuerda que, para factorizar la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más dos elevado al cuadrado, la raíz cuadrada es el binomio equis más dos, también extraes la raíz cuadrada de 1, la cual es uno.

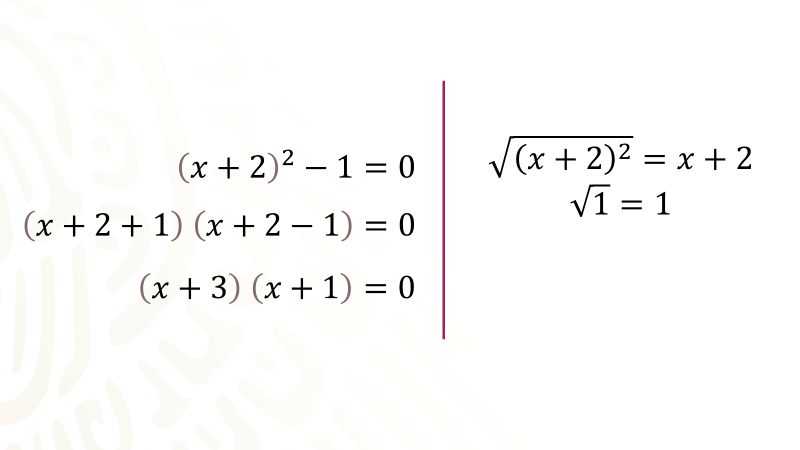
Para continuar preparas un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribe como primer término en los dos factores, la primera raíz, equis más dos; luego escribes como segundo término la segunda raíz, que es uno, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis más dos más uno y en el segundo factor queda equis más dos menos uno, continúas reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Ahora la respuesta a la interrogante ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta?

Para eso, utilizarás la propiedad del producto cero, la cual, simplemente establece que si ab = 0, a por be es igual acero, entonces puede suceder que:

• Que el factor “a” sea igual a cero.
• Que el factor “b” sea igual a cero.

También puede suceder que ambos factores sean igual a cero. Lo anterior significa que debes igualar cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más tres igual a cero y el binomio equis más uno igual a cero.

Después de resolver la ecuación de primer grado, equis más tres igual con cero, obtienes el valor de la primera raíz que es equis igual a tres negativo.

Si ahora resuelves la ecuación de primer grado, equis más uno igual con cero, obtienes el valor de la segunda raíz que es equis igual a uno negativo.

Has resuelto la ecuación de segundo grado propuesta utilizando el método de factorización y un procedimiento especial conocido como “completar el trinomio cuadrado perfecto”.

Para entender este nuevo procedimiento especial de completar un trinomio cuadrado perfecto utilizado para resolver ecuaciones de segundo grado mediante factorización, observa el siguiente ejemplo:

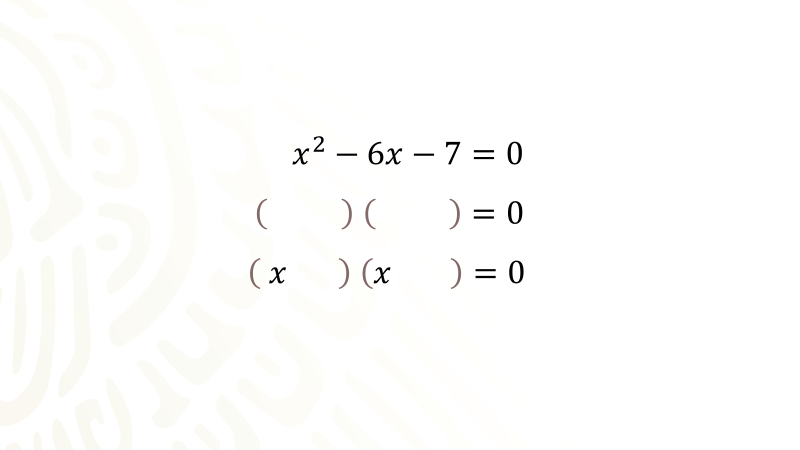
Cómo puedes observar esta ecuación tiene la forma “a equis cuadrada más be equis más ce igual a cero” donde en el término cuadrático “a es igual a uno”, el término de primer grado es seis equis negativo y el término numérico es siete negativo; esta ecuación la resolverás factorizándola utilizando el procedimiento de transformar el trinomio que se encuentra en el primer miembro de la ecuación como un trinomio cuadrado perfecto, es importante hacer algunas precisiones para favorecer que se entienda de mejor manera el procedimiento propuesto por Eduardo en la situación anterior.

El trinomio que se encuentra en el primer miembro de la ecuación dada se puede factorizar con un procedimiento que ya conoces, sin embargo, lo interesante de las matemáticas es que puede haber varios procedimientos para resolver determinadas situaciones, en este caso, estas estudiando ¿cómo completar un trinomio para que sea cuadrado perfecto?

Para dar sentido al uso de este nuevo procedimiento primero recuerda el procedimiento que ya conoces con la finalidad de que puedas verificar que los valores obtenidos de las raíces de las ecuaciones son los mismos que se obtienen con el nuevo procedimiento.

Tienes la ecuación:

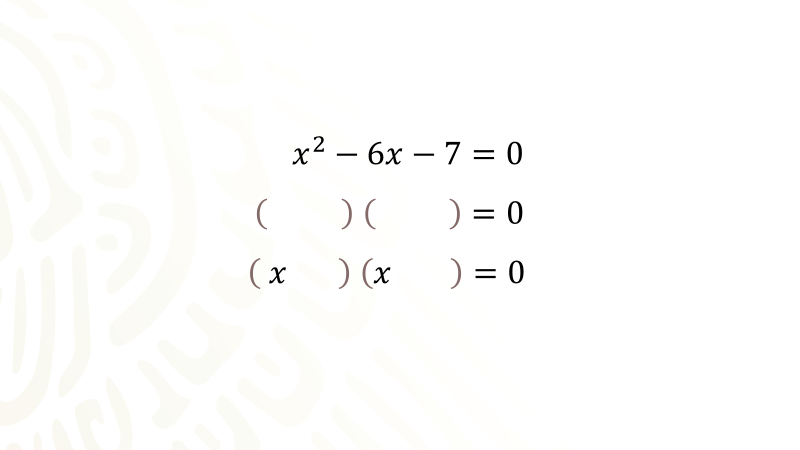
Preparas un par de paréntesis para formar un producto de binomios igualados con cero. El siguiente paso es extraer la raíz cuadrada del término cuadrático, en este trinomio la raíz cuadrada de equis cuadrada es equis, la escribes como primer término en cada binomio:

Ahora, necesitas determinar dos números considerando sus respectivos signos (positivo o negativo) que al mismo tiempo multiplicados den como resultado el valor del término numérico, es decir, siete con signo negativo y que sumados den como resultado seis con signo negativo.

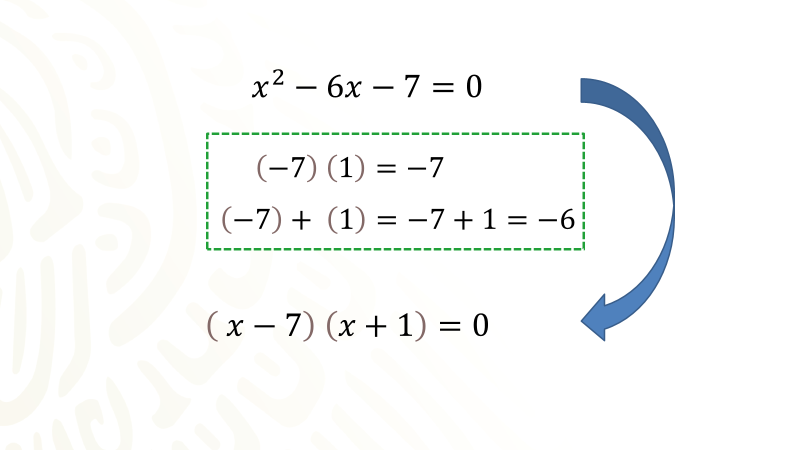
Recuerda que para determinar dichos números puedes apoyarte en la factorización del término numérico, en este caso, necesitas dos números que al multiplicarlos el producto sea un siete negativo, por lo que, uno de los números será positivo y el otro número será negativo, de las opciones posibles, elegirás la que también cumpla con que dichos números sumados den como resultado seis negativo, esto último nos indica que en realidad se restan los valores absolutos de dos números donde el de mayor valor es negativo.

Entonces al multiplicar siete con signo negativo por uno con signo positivo obtienes como resultado siete con signo negativo.

Por otra parte, al sumar el número siete negativo más el número uno positivo da como resultado seis negativo.

Anota como segundo término del primer factor binomio al siete negativo y como segundo término del segundo factor binomio al uno positivo, quedando, el indicado el producto del binomio equis menos siete por el binomio equis más uno igual a cero.

Cómo puedes observar se tiene la forma factorizada de la ecuación dada, sin embargo no se tiene en el primer miembro un producto indicado de binomios semejantes que también se puede expresar como un binomio al cuadrado que a su vez es equivalente con un Trinomio Cuadrado Perfecto, lo cual, permite afirmar que no se puede construir de manera geométrica, un cuadrado perfecto ya que las dimensiones de los lados no son valores iguales, lo que requiere es utilizar el procedimiento para completar el trinomio cuadrado perfecto.

Retoma la ecuación dada en su forma general: equis cuadrada menos seis equis menos siete igual a cero, escribes en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego menos siete igual a cero.

Obtienes la mitad del coeficiente del término de primer grado, seis entre dos es igual a tres, dicho valor ahora se eleva al cuadrado y se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumas nueve también restas nueve, lo que significa que has sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos seis equis más nueve menos nueve menos siete igual a cero.

Tienes ahora el Trinomio Cuadrado Perfecto: Equis cuadrada menos seis equis más nueve. Y además es equivalente con un binomio al cuadrado, ahora escribes dicho binomio menos nueve menos siete igual a cero.

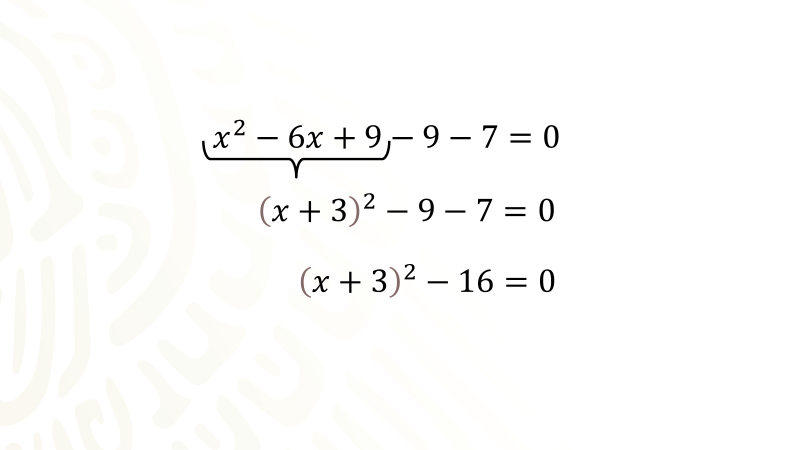
A continuación, se reducen los términos numéricos, quedando el binomio equis más tres al cuadrado menos dieciséis igual a cero.

A partir de ahí, puedes continuar resolviendo la ecuación ya sea recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación o bien despejando la incógnita para determinar los valores de las raíces de equis.

En esta ocasión, factorizarás la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más tres elevado al cuadrado, la raíz cuadrada es el binomio equis más tres, también extraes la raíz cuadrada de dieciséis, la cual es cuatro.

Ahora prepara un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribes como primer término en los dos factores, la primera raíz, equis más tres; luego escribes como segundo término la segunda raíz, que es cuatro, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis más tres más cuatro y en el segundo factor queda equis más tres menos cuatro, continúa reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Pero, este producto de binomios igualados con cero ya lo habías obtenido cuando se utilizó el primer procedimiento, esa era la finalidad, que te dieras cuenta que aprender otros procedimientos es muy útil y más al estudiar matemáticas.

Todavía falta determinar ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta?

Para eso, utilizarás la propiedad del producto cero, que explicas al resolver el primer ejemplo, la cual puedes resumir así: un producto de factores es cero si y sólo si uno o más de los factores es cero. Esta propiedad es particularmente útil cuando resuelven ecuaciones cuadráticas

Lo anterior significa que debes igualar cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más siete igual a cero y el binomio equis menos uno igual a cero

Después de resolver la ecuación de primer grado, equis más siete igual con cero, obtienes el valor de la primera raíz que es, equis igual a siete negativo. Si ahora, resuelves la ecuación de primer grado, equis menos uno igual con cero, obtienes el valor de la segunda raíz que es, equis igual a uno.

Has resuelto la ecuación de segundo grado propuesta utilizando el método de factorización y un procedimiento especial conocido como “completar el trinomio cuadrado perfecto”.

Sin embargo, debes hacer notar lo siguiente:

Como resultado del procedimiento utilizado para transformar la ecuación dada a otra donde se completó el trinomio como cuadrado perfecto, se realizó con base en considerar que el binomio equis cuadrada menos seis equis en la ecuación equis cuadrada menos seis equis menos siete igual a cero es equivalente con la expresión formada por el binomio equis más tres al cuadrado menos nueve en la ecuación obtenida que es equis cuadrada más tres al cuadrado menos nueve menos siete igual a cero.

Entonces es necesario preguntarse ¿Cómo verificar de manera geométrica la equivalencia de ambas expresiones? ¿Y cómo se puede verificar la equivalencia de las expresiones profesora?

Moldea las expresiones de la equivalencia propuesta para verificar si es verdadera.

Primero factoriza el binomio escrito en el primer miembro de la igualdad, equis cuadrada menos seis equis, queda factorizado como equis que multiplica al binomio equis más seis.

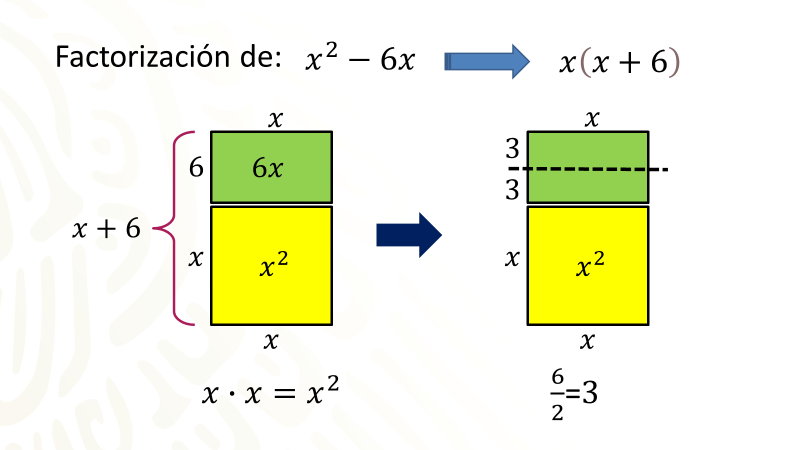
Ahora dibuja un modelo geométrico, tienes equis cuadrada, es decir, puedes dibujar un cuadrado cuyos lados miden equis, luego sabes que la factorización indica que uno de los lados mide equis y el otro lado mide equis más seis, el procedimiento algebraico indica que se divida entre dos el coeficiente del término de primer grado, esto es, dividir seis entre dos, obteniendo como cociente tres. En el modelo geométrico se divide con una línea punteada la longitud seis en dos partes iguales.

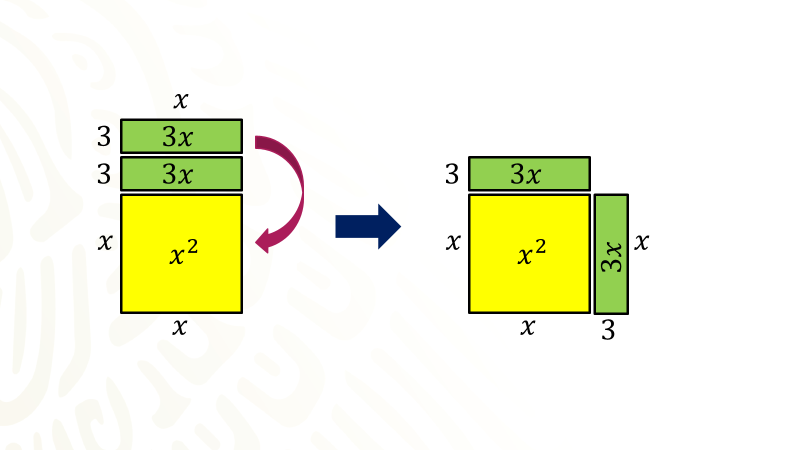
Se tienen dos rectángulos cuyos lados miden tres por equis; ahora traslada uno de los rectángulos para ponerlo a un lado del cuadrado en posición vertical, como puedes observar se tiene un cuadrado incompleto, ahora tienes la representación de la expresión algebraica equis cuadrada menos seis equis.

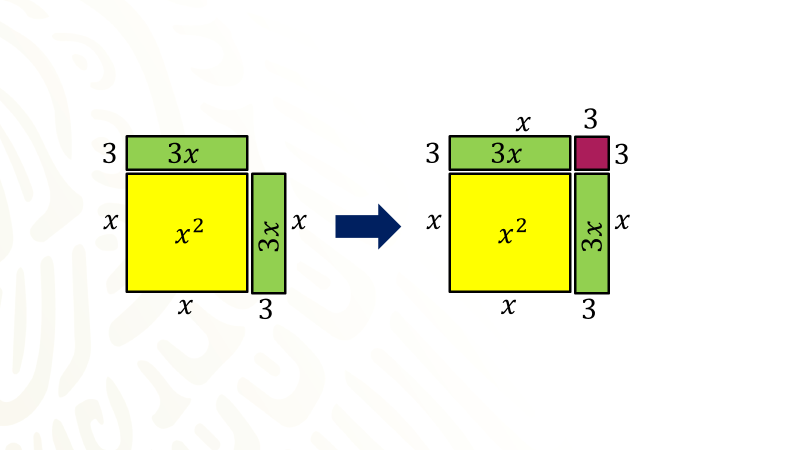
Trabaja con la interpretación de la expresión escrita en el segundo miembro de la igualdad que es el binomio equis más tres al cuadrado menos nueve, como puedes observar el cuadrado, cada lado ahora mide equis más tres, sin embargo es un cuadrado incompleto, en el procedimiento algebraico al dividir seis entre dos, se obtuvo tres como cociente, dicho valor se elevó al cuadrado obteniendo nueve, el cual se sumó para completar el trinomio y fuera un cuadrado perfecto, como se muestra en el modelo.

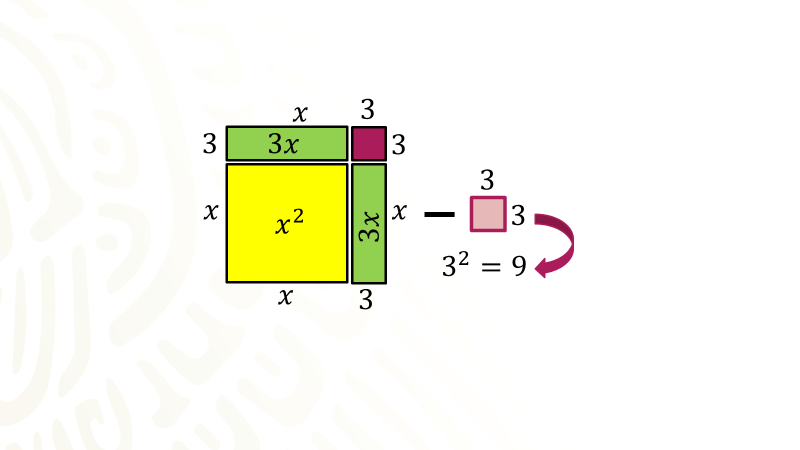
Pero recuerda que no sólo se suma el nueve también se resta nueve para evitar romper el equilibrio de la ecuación, dado que nueve menos nueve es cero, el modelo obtenido representa la expresión formada por el binomio equis más tres al cuadrado menos nueve.

De esta manera has verificado de manera geométrica que la expresión seis equis cuadrada más seis equis si es equivalente con la expresión formada por el binomio equis más tres al cuadrado menos nueve dando sentido al procedimiento de completar un trinomio como cuadrado perfecto.

Resuelve ahora una ecuación de segundo grado donde el coeficiente del término cuadrado no es igual a uno, la ecuación es:

Es recomendable, que de ser posible siempre trata de simplificar las expresiones matemáticas, en este caso, los números que forman parte de los tres términos del trinomio que se encuentra en el primer miembro de la ecuación son múltiplos de dos y por lo tanto son divisibles entre dos.

Antes de simplificar la ecuación dada, les recomiendo ordenar los términos del primer miembro de la ecuación de tal manera que en la primera posición este escrito el término cuadrático, en la segunda posición este escrito el término de primer grado y en la tercera posición este escrito el término numérico, después el trinomio es igualado con cero.

Para continuar divide entre dos negativo ambos miembros de la ecuación y con ello cada término que forma los dos miembros de la misma.

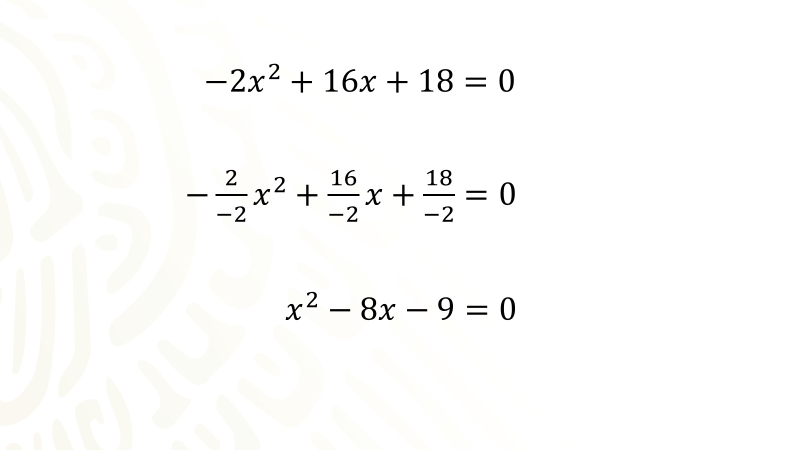
La intención es que el término cuadrático se transforme en positivo. Dos equis cuadrada negativo entre dos negativo se obtiene equis cuadrada; luego al dividir dieciséis equis entre dos negativo se obtiene ocho equis negativo, y al dividir dieciocho entre dos negativo se obtiene nueve negativo, finalmente al dividir cero ente dos negativo se obtiene cero. La ecuación equis cuadrada menos ocho equis menos nueve igual a cero que se obtuvo es equivalente a la primera.

Comienza completando el trinomio equis cuadrada menos ocho equis menos nueve en la ecuación donde el segundo miembro es cero, operarás con el binomio equis cuadrada menos ocho equis, escribe en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego menos nueve igual a cero.

Para continuar con el procedimiento, obtienes la mitad del coeficiente del término de primer grado, cuatro entre dos es igual a dos, dicho valor ahora se eleva al cuadrado y el valor obtenido se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumas dieciséis también restas dieciséis, lo que significa que has sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos ocho equis más dieciséis menos dieciséis menos nueve igual a cero.

El Trinomio Cuadrado Perfecto es: Equis cuadrada menos ocho equis más dieciséis. Y además es equivalente a tener un binomio al cuadrado, en este caso el trinomio equis cuadrada menos ocho equis más dieciséis es equivalente con el Binomio equis menos cuatro al cuadrado

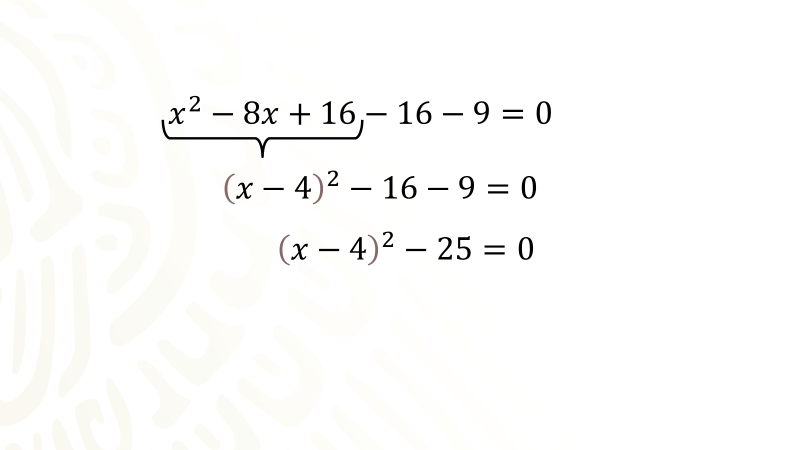
Después de tener el binomio al cuadrado ahora escribe menos dieciséis, menos nueve igual a cero. A continuación, se reducen los términos numéricos, quedando el binomio equis más cuatro al cuadrado menos veinticinco igual a cero.

A partir de aquí, puedes continuar resolviendo la ecuación recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación para determinar los valores de las raíces de equis.

Es importante tener presente que, para factorizar la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más dos elevado al cuadrado; la raíz cuadrada es el binomio equis más dos, también extraes la raíz cuadrada de 1, la cual es uno.

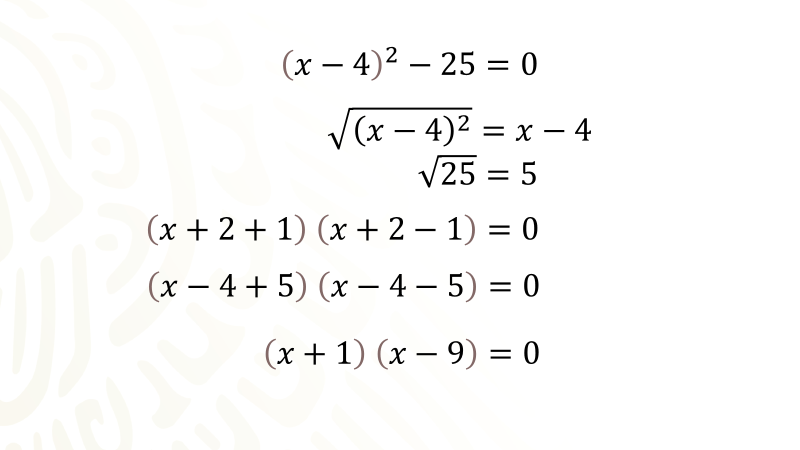
Para continuar preparas un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribes, como primer término en los dos factores, la primera raíz, equis menos cuatro; luego escribes como segundo término la segunda raíz, que es cinco, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis menos cuatro más cinco y en el segundo factor queda equis menos cuatro menos cinco, continúa reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Pero, ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta? Para eso, utilizarás la propiedad del producto cero, que ya conoces, entonces igualas cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más uno igual a cero y el binomio equis menos nueve igual a cero.

Después de resolver la ecuación de primer grado, equis más uno igual con cero, obtienes el valor de la primera raíz que es, equis igual a nueve negativo.

Si ahora resuelves la ecuación de primer grado, equis menos nueve igual con cero, obtienes el valor de la segunda raíz que es equis igual a uno. Pero ¿cómo puedes saber si los valores obtenidos como raíces de la ecuación de segundo grado dada la hacen verdadera?

Recuerda que para verificar si los valores obtenidos como raíces de la ecuación de segundo grado dada la hacen verdadera, es necesario sustituir dichos valores en la ecuación, por ejemplo: al sustituir el valor de equis igual a uno negativo en la ecuación original que es dos equis cuadrada negativo más dieciséis equis más dieciocho igual a cero, después de realizar las operaciones queda de la siguiente manera:

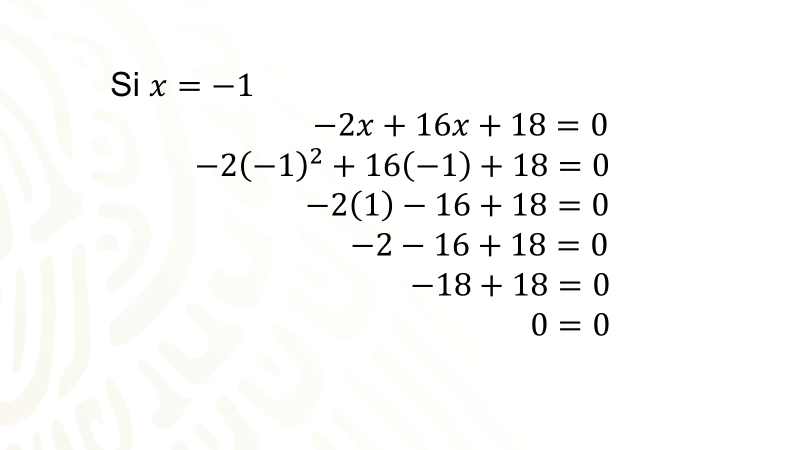
El reto de hoy:

Efectúa la verificación utilizando la ecuación original o la ecuación equivalente obtenida para cuando equis es igual a nueve. Consulta tu libro de texto de Matemáticas de tercer grado, ahí encontrarás otras actividades que te ayudarán a profundizar en este tema.

Es de mucha utilidad que pongas en práctica todo lo aprendido en la clase. Y un gran apoyo, es tu libro de texto.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/