Combinadas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Combinadas
Aprendizaje esperado: exploración de distintos significados de la multiplicación (relación proporcional entre medidas, producto de medidas, combinatoria) y desarrollo de procedimientos para el cálculo mental o escrito.
Énfasis: utilizar la multiplicación para resolver problemas que implican un producto entre medidas.
¿Qué vamos a aprender?
Trabajarás con el tema de combinaciones y con el uso de los organizadores gráficos que ya conoces.
En la sesión anterior trabajaste con tablas de doble entrada y diagrama de árbol, ¿recuerdas?
Si tienes libros en casa sobre el tema, o cuentas con Internet, explóralos para saber más.
¿Qué hacemos?
Analiza y resuelve la siguiente situación:
Si tenemos 2 shorts y 3 gorras diferentes, ¿cuántas combinaciones podemos obtener?

Se puede calcular el resultado de una forma rápida multiplicando los dos shorts por las tres gorras.
Y también puedes identificar las combinaciones posibles mediante un diagrama de árbol.
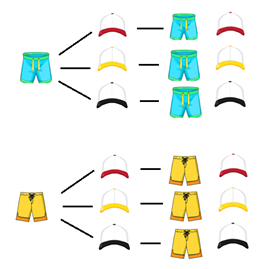
Analiza y resuelve la siguiente situación:
Para la fiesta de cumpleaños de Antonio, asistirán 18 mujeres y 15 hombres. ¿Cuántas parejas de baile se podrán formar con los invitados?
Para resolverlo debes multiplicar o para poder llegar a la solución.
Respecto a los procedimientos del cálculo, en este problema se pueden aplicar algunas estrategias como las siguientes:
- Se puede multiplicar el número de mujeres por el número de hombres que asistirán al baile.
- Se puede calcular mediante una notación multiplicativa, en la que, por ejemplo, se presenta una descomposición en el número de hombres que asistirán en decenas y unidades, lo que puede facilitar inclusive que realices un cálculo mental:

Analiza y resuelve la siguiente situación:
En una fonda tienen el siguiente menú

¿Cuántas combinaciones del menú podemos obtener?
Para saber la cantidad de combinaciones, se pueden multiplicar el número de cada una de las opciones, es decir, multiplicar 3 entradas por 3 platos principales:
Se obtienen 9 combinaciones, que puedes identificar en el siguiente diagrama de árbol.
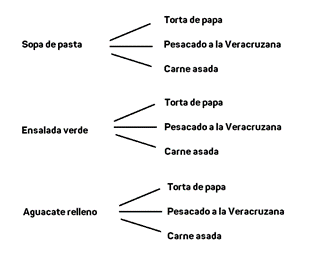
Analiza y resuelve la siguiente situación:
¿Cuántas combinaciones de ropa podemos hacer con dos blusas y tres faldas?

Observando la información en la tabla se puede saber que puedes obtener 6 cambios de ropa.
Es muy importante que recuerdes que puedes realizar el cálculo de este resultado de una forma más rápida, mediante la multiplicación de los datos que definen las opciones. En este ejemplo el número de blusas y el número de faldas:
Si te apoyas en la tabla para corroborar el resultado, verás que se tienen las siguientes combinaciones:

Este tipo de problemas, como los que has resuelto en clases anteriores, comparten en su proceso de solución el uso de la multiplicación, por lo que esta operación representa una herramienta matemática muy útil para distintas situaciones.
Recuerda otros tipos de problemas en los que la multiplicación te puede servir como herramienta de solución, por ejemplo:
SITUACIONES DE PORPORCIONALIDAD, es decir, aquellas que llevan a calcular un valor que no se conoce, a partir de datos que sí se conocen. Como cuando calculas ingredientes de una receta para una cantidad de comensales.
Para para que dos magnitudes mantengan una relación de proporcionalidad, si se aumenta multiplicativamente una, la otra tiene que aumentar multiplicativamente en la misma proporción: al doble, al triple, etc. Si se reduce una de forma partitiva: a la mitad, la tercera parte, etc., la otra también se tiene que reducir en la misma proporción.
Se puede decir que, si se cambia la cantidad de una de las magnitudes, se tiene que cambiar la cantidad de las otras si se quiere mantener la relación de proporcionalidad entre ellas.
Recuerda cómo se aplica, resolviendo la siguiente situación:

Si se requiere conocer qué cantidad de naranjas se necesitan para obtener hasta 6 litros de jugo, puedes organizar la información de la manera siguiente:

Para conocer los datos faltantes debes multiplicar el número de naranjas que se requiere para la cantidad de jugo:

Como puedes ver, aquí la proporción es 7 naranjas por cada litro que se quiera obtener.
Aquí 7 naranjas es el valor unitario del problema.
En otras sesiones aprendiste que este concepto hace referencia a la relación de dos magnitudes, cuando una de ellas es la unidad o sea 1.
Resuelve la siguiente situación:
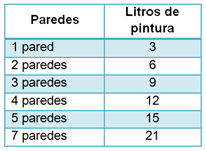
Cuántos litros de pintura se necesitan para pintar una pared, si para pintar 4 paredes se requieren 12 litros.
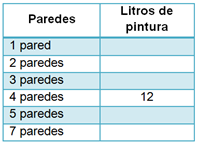
Se puede comenzar calculando una disminución proporcional de la información.
Comienza calculando la mitad, lo cual implica dividir entre 2 los datos:

Para pintar una pared se necesitan 3 litros.
Como se ha calculado el valor unitario, se puede entonces también saber cuánto se necesita de pintura para el resto de los casos. Para ello multiplicas el valor unitario por la cantidad de pared que interese.
Por ejemplo, la pintura necesaria para pintar 7 paredes se calcula multiplicando , lo que da 21 litros de pintura.
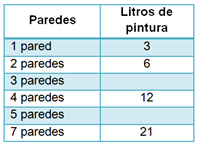
Algo más que ya has aprendido es que puedes utilizar las proporciones que conoces para calcular algunas faltantes. Por ejemplo, para conocer los litros de pintura que se necesitan para pintar 3 paredes, también puedes sumar la información relacionada con 1 pared y 2 paredes. Así, sumando los litros respectivos: , se tiene que se necesitan 9 litros de pintura.
En el caso de la cantidad de litros que se requiere para pintar 5 paredes, se puede emplear el valor unitario que ya conoces y multiplicar , lo que da como resultado 15 litros; y también podrías sumar 5 veces esta cantidad:
Aunque es más tardado y menos práctico que el uso del valor unitario.
El día de hoy repasaste el uso de tablas de doble entrada y el diagrama de árbol. También recordaste la aplicación de la proporcionalidad. Recuerda:
La multiplicación es una herramienta matemática que te permite realizar cálculos de forma más práctica y eficaz, por ejemplo, las situaciones de conteo y proporcionalidad que hemos revisado.
En el caso de las situaciones de conteo utilizar un organizador gráfico, como las tablas de doble entrada o los diagramas de árbol, te permite mostrar de mejor manera tus posibilidades de combinar productos u objetos, así como obtener las respuestas a algunas preguntas de manera más fácil.
El concepto de proporción implica que tengas muy clara la relación numérica que existe entre 2 magnitudes, tanto si aumentan o disminuyen y en qué proporción lo hacen.
El reto de hoy:
Resuelve la siguiente situación.
Margarita desea preparar diferentes tipos de ensaladas; si ella tiene tres diferentes tipos de aderezo y tres clases de complementos, ¿Cuántos tipos de ensalada puede hacer?
Plática con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
¡Buen trabajo!
Gracias por tu esfuerzo
Para saber más:
Lecturas





Login to join the discussion