Cociente de potencias de la misma base

Aprendizaje esperado: resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas.

Énfasis : elaborar, utilizar y justificar procedimientos para calcular cocientes de potencias enteras de la misma base.

¿Qué vamos a aprender?

Continuarás con el estudio de potencias. En esta sesión, estudiarás el cociente de potencias enteras de la misma base. Para ello, elaborarás, utilizarás y justificarás los procedimientos necesarios.

¿Qué hacemos?

Para iniciar, analiza y resuelve la siguiente situación.

Situación-problema, bipartición de células

La reproducción más usual de una célula bacteriana se realiza con la bipartición; es decir, la división de una célula en dos. Cada una de estas células, a su vez se divide en dos, y así sucesivamente. Al cabo de cierto tiempo, las células se han reproducido y esto es parte de lo que se conoce como reproducción celular.

Para esta situación, considera comenzar con una célula, ¿cuántas células se tienen cuando se ha llevado a cabo este proceso 3, 4, 5, o “n” veces?

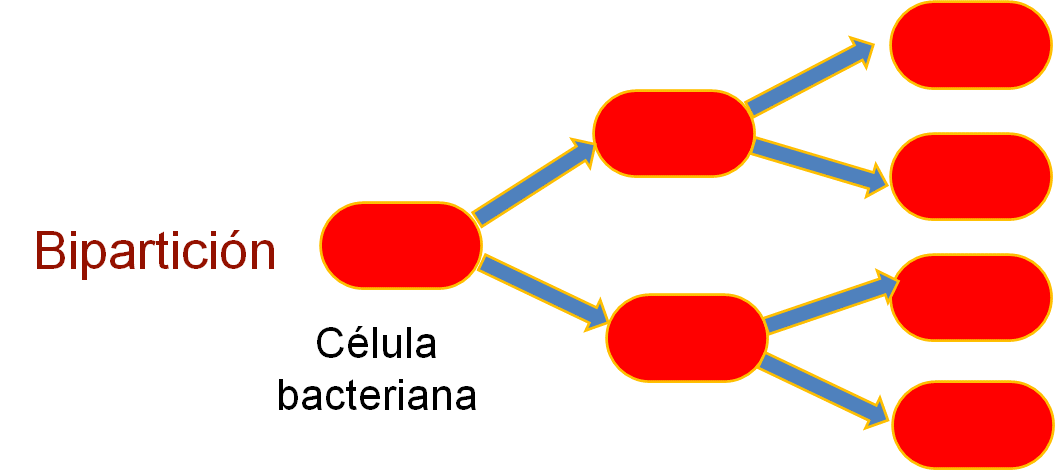
Inicialmente se tiene una célula, cuando esa célula se divide la primera vez hay 2 células, en la segunda partición hay 4 células, en la tercera partición son 8 células, en la cuarta partición son 16 células y en la quinta partición son 32 células.

¿Cómo puedes obtener una generalización para “n” biparticiones, es decir, para “n” veces?

Analiza. Al comenzar con una célula, ésta se multiplica por dos en la primera bipartición. En la segunda bipartición, dos se multiplica por 2 para llegar a 4 células. En la tercera bipartición, 4 se multiplica por 2 para llegar a 8 células; en la cuarta bipartición 8 se multiplica por dos para llegar a 16 células; en la quinta bipartición 16 se multiplica por dos para llegar a 32 células, y así sucesivamente.

Ya que siempre se multiplica por dos para obtener el número de células que se van reproduciendo, se pueden expresar los resultados de la tabla en potencias de 2.

Se sabe que, en una potencia, el exponente es el número de veces que se multiplica a la base por sí misma.

De ahí que cuatro se puede representar como dos por dos, es decir, dos al cuadrado; de la misma forma 8 es igual a dos por dos por dos, que es igual a dos al cubo. Por lo tanto, a 16 se puede representar como dos a la cuarta, y 32 como dos a la quinta. Por otro lado, considera que dos representado en forma de potencia es dos a la uno. Y siguiendo la tendencia debes tomar en cuenta que cualquier número (excepto el cero) elevado a la cero es uno, en este caso, dos a la cero.

¿Qué se puede sugerir al comparar el número de particiones, con el exponente en la representación del número de células en forma de potencias?

Seguramente ya identificaste que el exponente es el número de veces en el que se ha dividido la célula desde que comienza la bipartición; entonces, dos a la “n” representa el número de células que hay en determinado momento, cuando la célula inicial se ha dividido “n” veces.

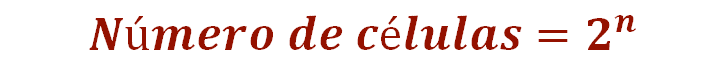
Entonces dos a la “n” es la generalización para la bipartición celular, cuando se comienza con una célula. Pero ¿cómo se aplica esta generalización?

Para ello, responde la siguiente pregunta:

¿Cuántas células se tienen después de que una célula se ha dividido 10, 20 o cien veces?

Utilizando la generalización, se puede obtener el número de células que hay, cuando la célula inicial se ha dividido 10 veces, se sustituye el valor de “n” igual a diez, en dos a la “n”. Entonces tienes que dos a la diez es multiplicar 2, diez veces por sí mismo.

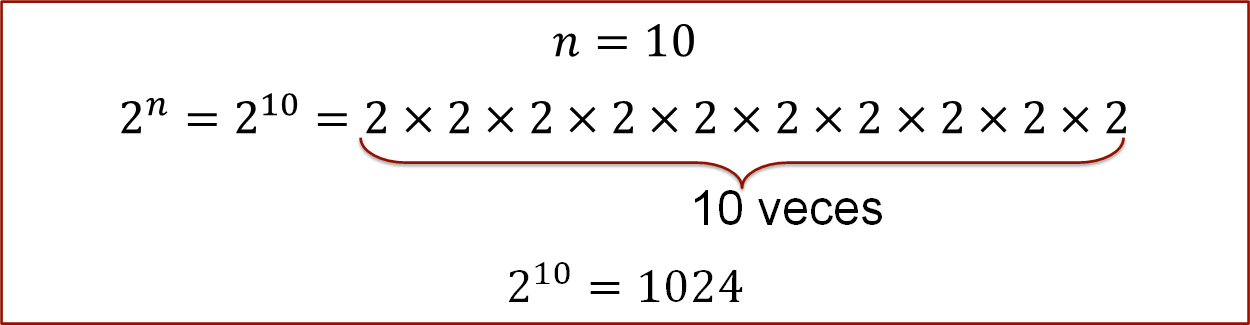
Resolviendo las multiplicaciones se tiene que dos a la diez es 1024, que representa a mil veinticuatro células.

Cuando “n” es igual a 20, al sustituirlo en la generalización, se tiene que dos a la veinte es igual a multiplicar dos por sí mismo veinte veces.

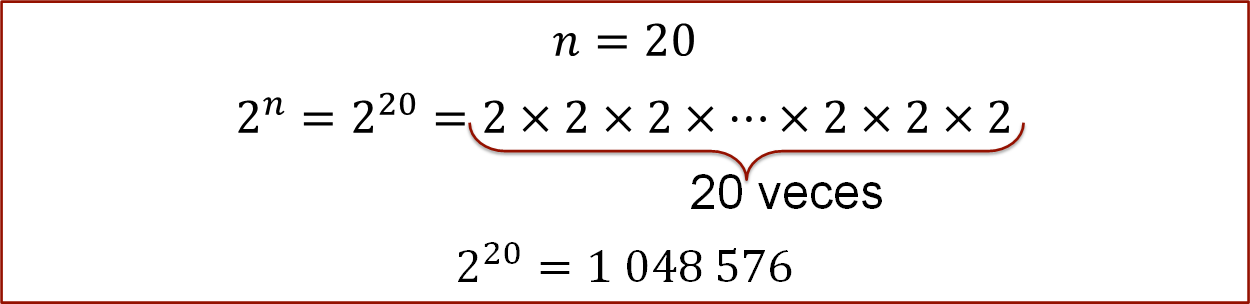
Resolviendo la operación se tiene que dos a la veinte es igual a un millón cuarenta y ocho mil quinientos setenta y seis células.

Y cuando “n” es igual a 100, dos a la cien es un número muy grande, tanto que es mejor dejarlo representado en forma de potencia, ya que al resolver la operación nos vemos en la necesidad de utilizar la notación científica para expresarlo.

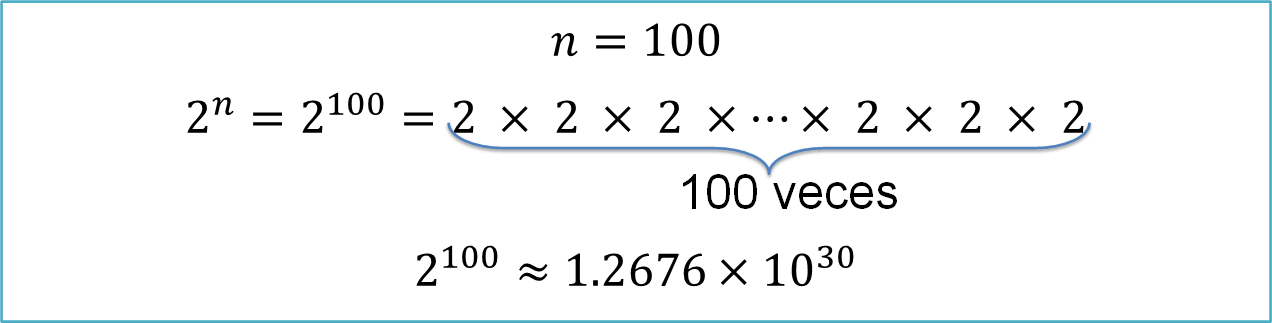
En este caso, dos a la cien es aproximadamente uno punto veintiséis setenta y seis, por diez a la treinta. Para darte una idea, para escribirlo tendrías doce mil seiscientos setenta y seis seguido de veintiséis cifras más.

Como puedes observar, es importante el estudio de las potencias, ya que se usan con mucha frecuencia para representar cantidades muy grandes, por ejemplo, las distancias astronómicas o algunas constantes físicas que aprenderás en tu vida de estudiante, como el número de Avogadro o el de la velocidad de la luz, que son representados en notación científica, en las que se representan a los números con factores que incluyen a potencias de diez.

Dicho lo anterior, resuelve la siguiente situación relacionada con distancias astronómicas.

Situación-problema, distancias astronómicas

Elsa y Joel se encontraban observando el cielo y se preguntaban entre ellos acerca de las distancias que hay entre los planetas, planetoides y el Sol.

Joel le pregunta a Elsa ¿cuántas veces será mayor la distancia del Sol a la Tierra que del Sol a Mercurio? Y ¿cuántas veces será mayor la distancia de Plutón al Sol que de Mercurio al Sol?

Joel reflexiona, y se pregunta ¿qué se necesita saber para contestar estas preguntas?

Para responder la primera pregunta, Elsa le indica a Joel que requieren saber cuál es la distancia del Sol a la Tierra, del Sol a Mercurio y realizar dicha comparación por medio de una razón o un cociente.

Joel busca información en algunos libros y se encuentra con la siguiente tabla:

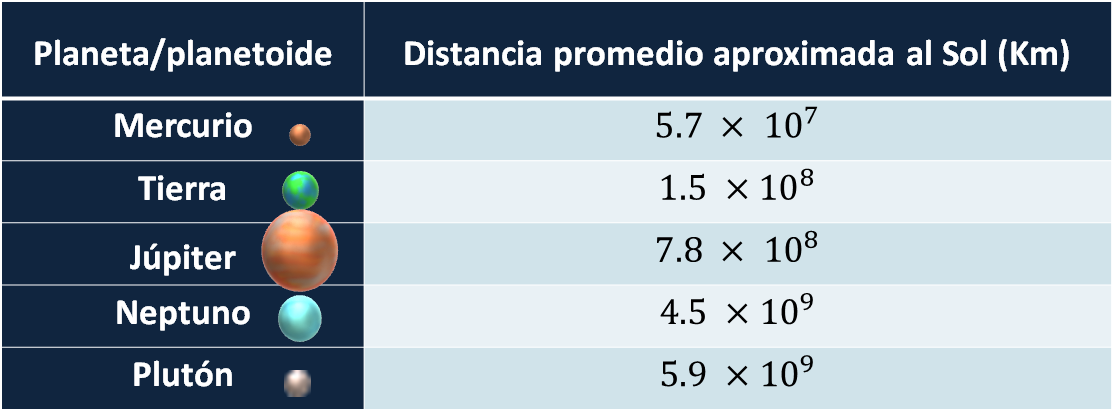
Elsa identifica en la tabla que la distancia promedio del Sol a la Tierra es de uno punto cinco por diez a la ocho, kilómetros. Esto quiere decir que hay momentos en que la Tierra está más cerca del Sol y en otros momentos está más lejos, por ello se requiere tomar un promedio de las distancias obtenidas a lo largo de los años. Lo mismo ocurre para los otros planetas.

Joel observa que las distancias están en una notación que no había utilizado, llamada notación científica, y para poder comparar las distancias es necesario que puedan interpretar esta notación.

Elsa se da cuenta de que la notación científica tiene un coeficiente multiplicado por una potencia de diez. Esto es, el coeficiente tiene una cifra entera, que en este caso es el uno y una cifra decimal, el cinco, todo esto multiplicado por una potencia de diez, que es diez elevado a la ocho.

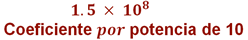
Pero ¿qué significa? Joel piensa que pueden desarrollar la multiplicación de 1.5 por 10 a la ocho, es decir, desarrollar la potencia de diez y multiplicarlo por 1.5, de la siguiente forma:

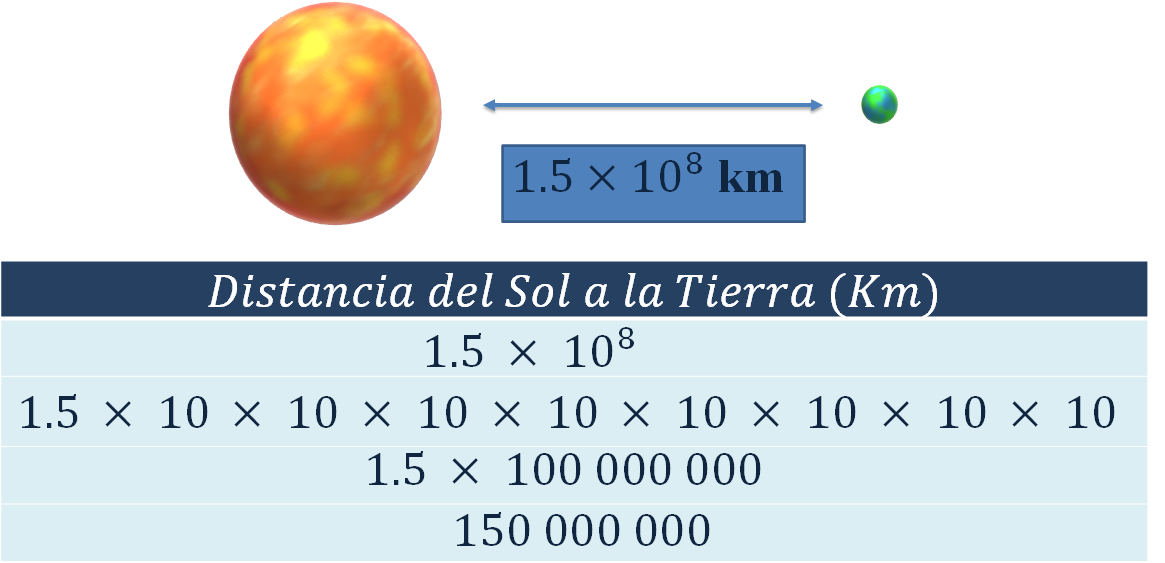
Como la distancia del Sol a la Tierra es de 1.5 por diez a la ocho, kilómetros; se tiene que 1.5 multiplicado por 10 ocho veces, es igual a 1.5 por cien millones, que a su vez es igual a 150 millones de kilómetros.

De la misma forma, Elsa identifica que la distancia del Sol a Mercurio es de 5.7 por diez a la siete, kilómetros. Esto es, 5.7 multiplicado por diez 7 veces, que es igual a 5.7 por diez millones, equivalente a cincuenta y siete millones de kilómetros.

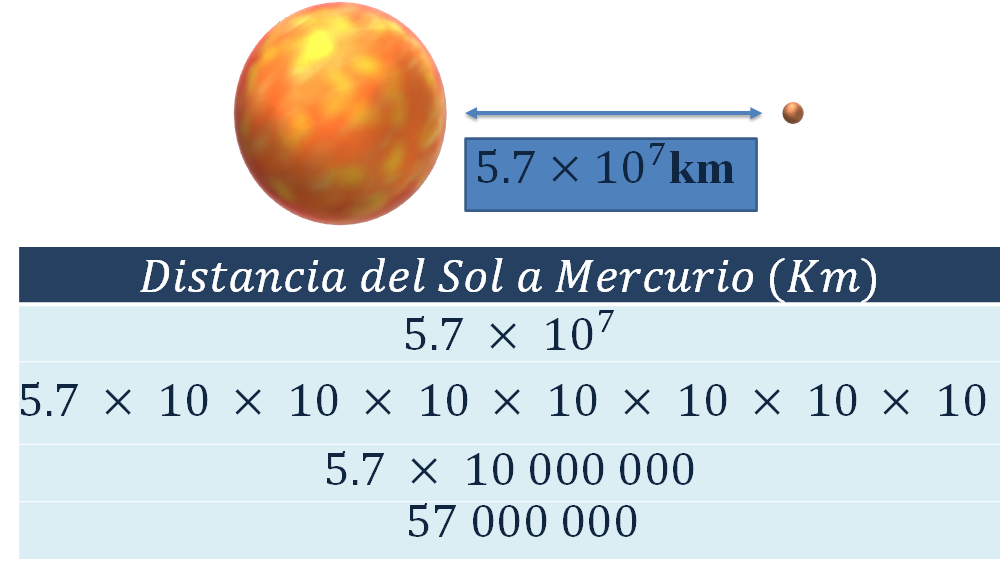
Joel piensa que la distancia del Sol a la Tierra es aproximadamente 3 veces mayor que la del Sol a Mercurio.

¿Tú qué piensas?

¿Cuántas veces es mayor la distancia del Sol a la Tierra que del Sol a Mercurio?

Para descubrirlo, debes obtener la relación de las distancias, dividiendo la distancia del Sol a la Tierra, entre la distancia del Sol a Mercurio. Esto es: 1.5 por diez a la ocho, entre 5.7 por diez a la siete, kilómetros, que es igual a ciento cincuenta millones entre cincuenta y siete millones, que aproximadamente es de 2.63.

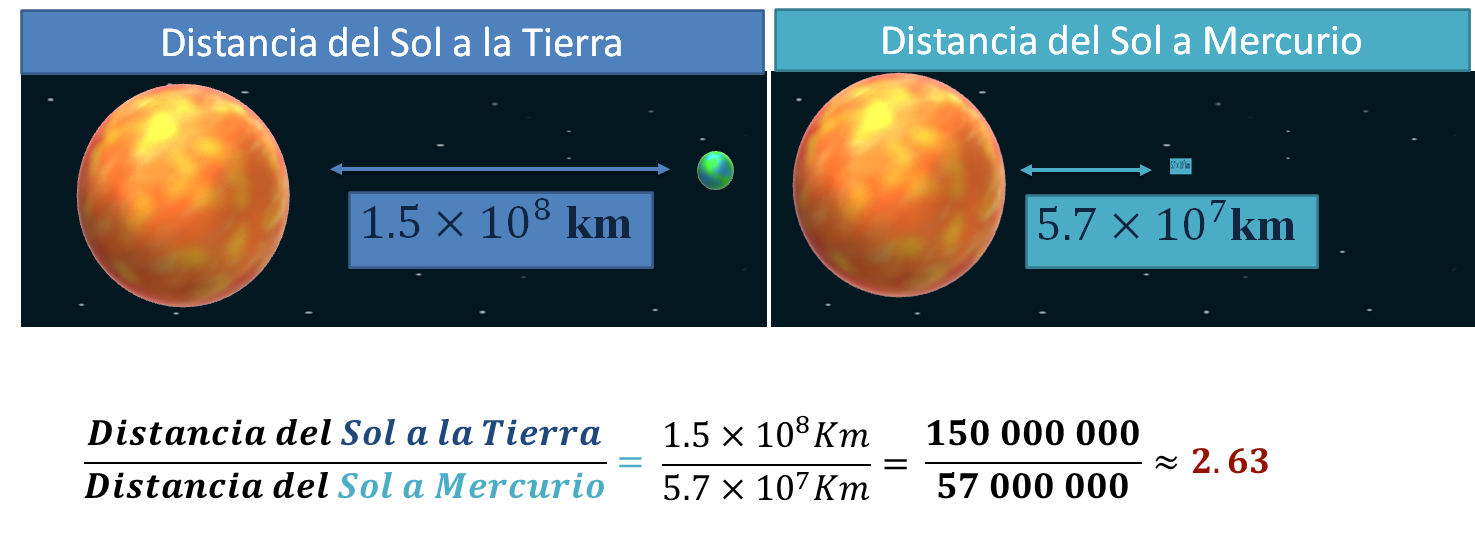
Esto quiere decir que la distancia del Sol a la Tierra es 2.63 veces mayor que la distancia del Sol a Mercurio.

Pero ¿cómo supo Joel que la distancia de la Tierra al Sol era aproximadamente tres veces mayor que la distancia de Mercurio al Sol?

Una forma de saberlo es analizando el cociente con las potencias de diez. Es decir, se desarrolla la potencia, sin realizar la multiplicación.

Entonces se tiene que 1.5 por diez a la ocho entre 5.7 por diez a la siete es igual a 1.5 multiplicado por diez, ocho veces, entre 5.7 multiplicado por diez, siete veces.

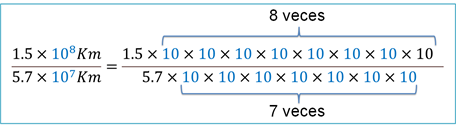
Reacomodando los factores se tiene siete iguales en el numerador y en el denominador.

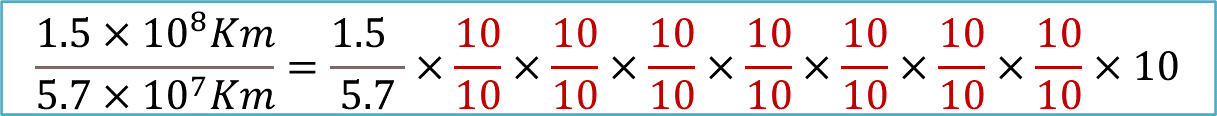
Estos factores que son iguales se simplifican, ya que al dividir diez entre diez se obtiene 1; por ello, la expresión simplificada es 1.5 entre 5.7 por 1, siete veces, y esto multiplicado por diez. Que a su vez es igual a 1.5 entre 5.7 por diez.

Que es igual a quince entre 5.7 y al realizar la división se tiene que, aproximadamente, es de 2.63.

Reflexiona acerca de lo que ocurrió con el cociente de las potencias de diez, contestando las siguientes preguntas:

¿Qué sucede al dividir diez a la ocho entre diez a la siete?

¿Cómo puedes obtener el resultado sin tener que desarrollar la potencia?

Diez a la ocho entre diez a la siete es igual a diez, multiplicado por sí mismo ocho veces entre diez, multiplicado por sí mismo siete veces.

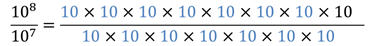
Al reacomodar los factores se tiene que hay siete factores iguales en el numerador y en el denominador que se simplifican, ya que al dividirse diez entre diez se obtiene uno.

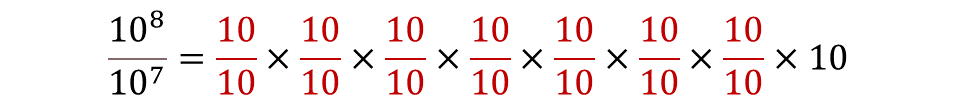
Quedando uno siete veces multiplicado por sí mismo por diez, que es un factor que no se simplificó.

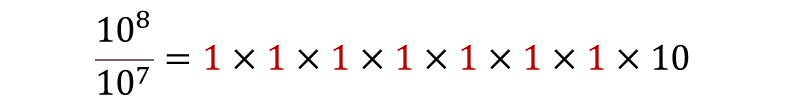
De tal forma que, al dividir diez a la ocho entre diez a la siete, se obtiene diez a la uno.

Es tiempo de analizar:

¿Cómo puedes obtener el cociente de potencias de la misma base sin desarrollar las potencias?

Elsa dice que si la base es la misma basta con restar los exponentes, es decir, como la base en el numerador y en el denominador es diez, se resta al exponente de la potencia del numerador, el exponente de la potencia del denominador. Quedando como resultado la misma base, pero el exponente de la potencia del numerador 8 se le resta el de la potencia del denominador 7 y se obtiene el exponente de la potencia del resultado 1, ya que 8 menos 7 es uno y como diez a la uno es diez, entonces el resultado es 10.

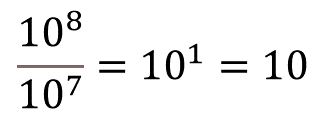
Regresando a la situación de Elsa y Joel, la de comparar las distancias de algunos planetas al Sol, se tiene que, para poder relacionar dos números con notación científica por medio de un cociente, se pueden resolver las operaciones que tienen la misma base, utilizando lo que has aprendido hasta este momento.

Para resolver la pregunta: ¿cuántas veces es mayor la distancia de Plutón al Sol que la de Mercurio al Sol?, realiza la comparación utilizando los datos de la tabla que encontró Joel.

La distancia de Plutón al Sol entre la distancia de Mercurio al Sol es igual a 5.9 por diez a la nueve, entre 5.7 por diez a la siete, kilómetros.

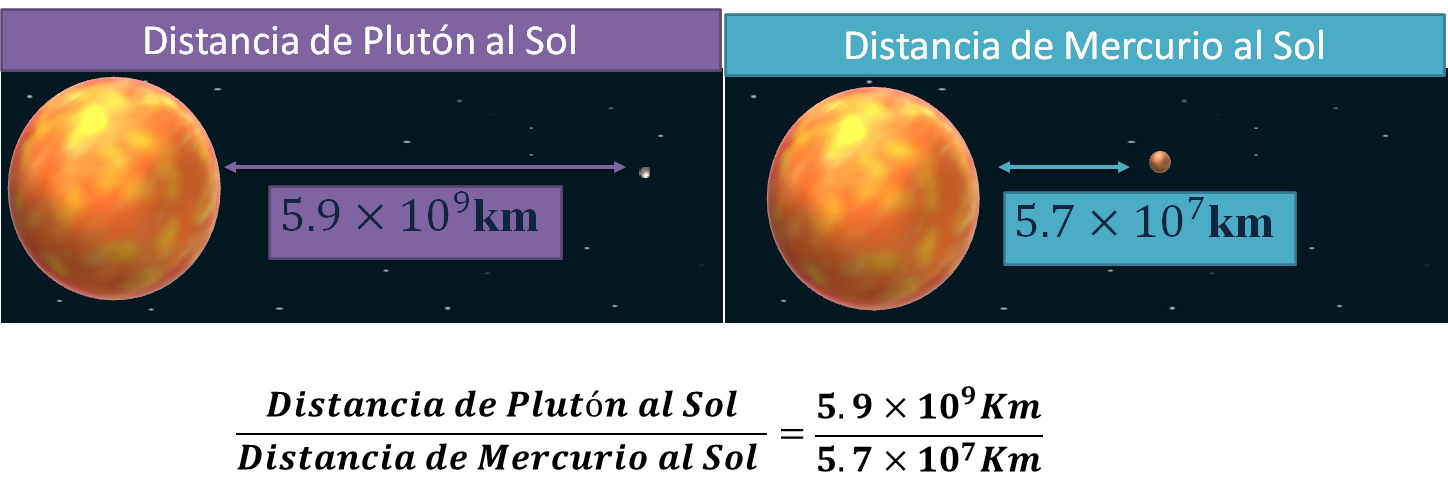
De acuerdo con lo que has revisado, puedes realizar las operaciones dividiendo los coeficientes 5.9 entre 5.7, y multiplicarlo por el cociente de las potencias de diez, es decir, diez a la nueve entre diez a la siete.

Al dividir los coeficientes 5.9 entre 5.7, da aproximadamente 1.035, por el resultado de dividir diez a la nueve entre diez a la siete que es diez a la dos.

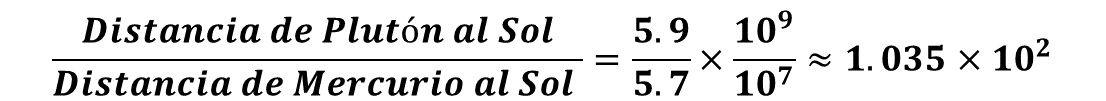
Resolviendo las operaciones se tiene que la distancia de Plutón al Sol entre la distancia de Mercurio al Sol es, aproximadamente, de 1.035 por diez a la dos, y como diez a la dos es cien, entonces esto es aproximadamente igual a 103.5

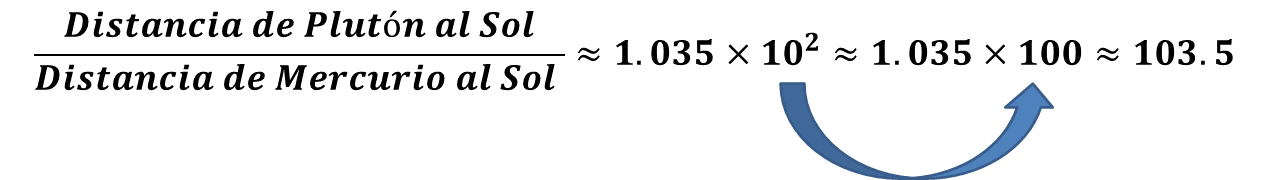
Esto significa que la distancia de Plutón al Sol es 103.5 veces mayor que la distancia de Mercurio al Sol.

Pero ¿cómo se sabe que diez a la nueve entre diez a la siete era diez a la dos?

Porque al dividir diez a la nueve entre diez a la siete, siete de los nueve factores que se encuentran en el numerador se simplifican con los siete factores iguales que hay en el del denominador. Quedando sólo dos factores de diez en el numerador. Esto se puede hacer porque tanto el numerador como el denominador tienen a la misma base, que es diez.

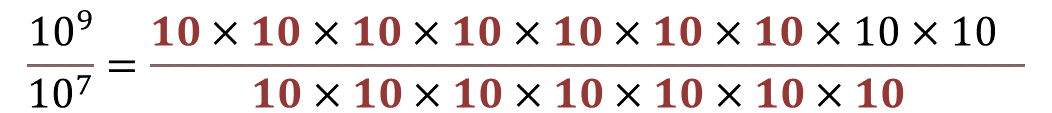
Reflexiona:

Si quieres resolver un cociente de potencias de la misma base, ¿qué operación debes realizar con los exponentes para obtener el exponente del resultado?

Seguramente identificaste que, si restas el exponente de la potencia del numerador 9, con el exponente de la potencia del denominador 7, se obtiene el exponente de la potencia del resultado.

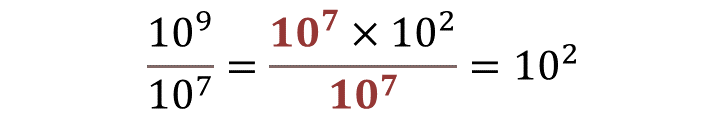
Has analizado que cuando se resuelve un cociente de potencias de diez, al dividir estas potencias, el resultado conserva la misma base, en este caso diez; y el exponente resulta de restar el exponente de la potencia del numerador menos el exponente de la potencia del denominador, en otras palabras, diez a la “m” entre diez a la “n” es igual a diez a la “m” menos “n”, donde “m” y “n” son números enteros.

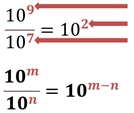
Pero ¿esto únicamente se puede aplicar cuando se trata de potencias de diez?

Para contestar esta pregunta, analiza un caso más y verifica si se puede generalizar para cualquier potencia. Reflexiona con el siguiente cuestionamiento:

¿Cómo se puede generalizar el cociente de potencias de la misma base?

Para poder generalizar debes percatarte, por lo menos con tres casos diferentes, que ocurre lo que sucedió anteriormente con las potencias de diez.

Analiza el siguiente cociente, seis a la diez entre seis al cubo. Seis a la diez es 6 multiplicado por sí mismo diez veces, es decir:

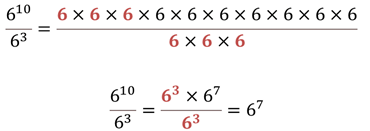
¿Cuántas veces pueden simplificarse los factores de 6? Se simplifican 3 veces, ya que tanto en el numerador como en el denominador se encuentran contenidos esos tres factores.

Por lo tanto, el resultado tiene la misma base de 6 que las potencias que se están dividiendo.

También puedes identificar que al restar 10 menos 3, los exponentes de las potencias del numerador y del denominador, respectivamente, se obtiene el exponente de la potencia del resultado, que es siete.

Hasta este momento has analizado tres casos diferentes, que diez a la ocho entre diez a la siete es igual a diez a la uno. También que diez a la nueve entre diez a la siete es igual a diez a la dos. Y que seis a la diez entre seis a la tres es seis a la siete.

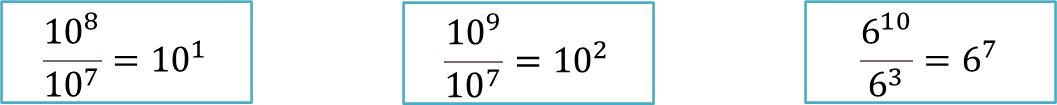
Con lo anterior, anota una regla general que indique cómo se resuelve un cociente de potencias con la misma base. Posteriormente, compártela con la que se presenta a continuación:

En un cociente, cuando el numerador y el denominador tienen la misma base, los exponentes se restan, es decir, al exponente de la potencia del numerador se le resta el exponente de la potencia del denominador, obteniendo así el exponente de la potencia del resultado, en otras palabras, “a” a la “m” entre “a” a la “n” es igual a: “a” a la “m” menos “n”.

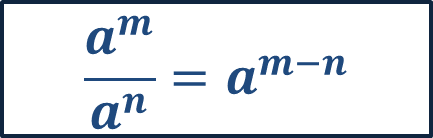
Esto quiere decir que sí puedes aplicar la generalización para potencias que tienen base diez o cualquier otra base.

Es frecuente que en Matemáticas como en otras asignaturas, como Física, Química o Biología, tengas que realizar operaciones que incluyen el cociente de potencias para resolver problemas, por ello es necesario que tengas presente la generalización que acabas de obtener.

Ahora aplica y comprueba la generalización para diferentes bases.

¿Cuántas veces es mayor cinco a la sexta potencia, que cinco a la cuarta potencia?

Para contestar esta pregunta es necesario dividir cinco a la sexta entre cinco a la cuarta. Como en el numerador y en el denominador se tiene a la misma base, entonces sí se puede aplicar la generalización, que “a” a la “m” entre “a” a la “n” es igual a “a” a la “m” menos “n”.

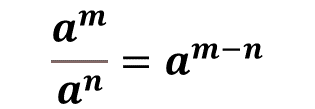
Entonces, cinco a la sexta entre cinco a la cuarta es igual a la base, que es 5 y su exponente será seis menos cuatro, esto es 2, es decir cinco al cuadrado.

Comprueba el resultado; como en el numerador está cinco a la sexta, están contenidos cuatro factores que se pueden simplificar con los cuatro factores iguales del denominador quedando dos factores de 5 en el numerador, por lo tanto, el resultado es cinco al cuadrado.

Como pudiste observar, si se aplica o no la generalización se obtiene el mismo resultado.

Pero ¿puedes aplicar la generalización, aunque la base sea un número positivo, negativo, decimal o en su forma fraccionaria?

Analiza el siguiente ejercicio.

¿Cuánto es (-3) a la cinco entre (-3) a la dos?

Como la base es (-3) tanto en el numerador como en el denominador, entonces sí se puede aplicar la generalización. El resultado será la misma base que es (-3) elevado a la cinco menos dos que es tres, entonces el resultado es (-3) al cubo.

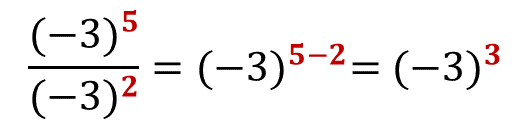
Comprueba el resultado, como en el numerador está (-3) a la quinta, ahí están contenidos los dos factores que se pueden simplificar con los dos factores iguales del denominador, quedando tres factores de (-3) en el numerador, por lo tanto, el resultado es (-3) al cubo.

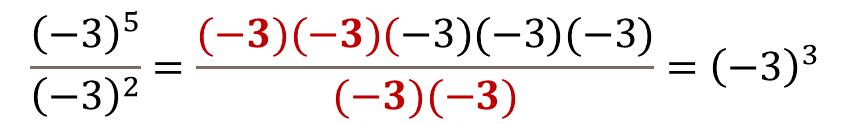
Como puedes observar, si se aplica o no, la generalización, se obtiene el mismo resultado. Entonces:

¿Cuál es la ventaja de tener una generalización?

Piensa cuándo la utilizarías y por qué.

Ahora verifica si la generalización la puedes utilizar para un número decimal.

¿Cuánto es (0.1) a la siete entre (0.1) a la cuarta?

Como la base es 0.1, tanto en el numerador como en el denominador, entonces sí si se puede aplicar la generalización. El resultado será la misma base, que es 0.1 uno elevado a la siete menos cuatro que es tres, entonces el resultado es 0.1 elevado al cubo.

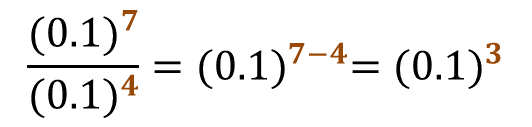
Comprueba el resultado, como en el numerador está 0.1 a la séptima, ahí están contenidos los cuatro factores que se pueden simplificar con los cuatro factores iguales del denominador, quedando tres factores de 0.1 en el numerador, por lo tanto, el resultado es 0.1 al cubo.

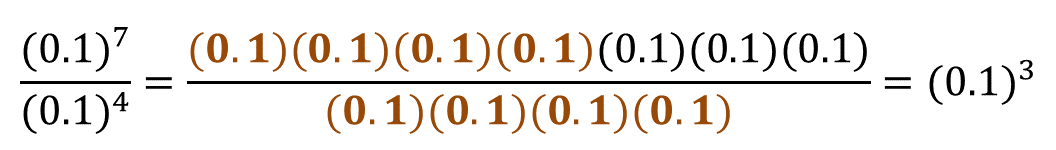
Si se aplica o no la generalización, se obtiene el mismo resultado, entonces la generalización sí es válida para cualquier base.

Finalmente, piensa:

¿Cómo resolverías el cociente “p” a la ochenta y nueve, entre “p” a la sesenta y cinco?

Seguramente, ya identificaste que “p” a la ochenta y nueve y “p” a la sesenta y cinco son muchas “p” multiplicadas por sí mismas, y para ahorrar el tiempo de escritura y los posibles errores que pudieran presentarse derivados de la misma escritura se aplica la generalización. Entonces, se tiene que “p” a la ochenta y nueve entre “p” a la sesenta y cinco es igual a “p” a la ochenta y nueve menos sesenta y cinco, que es igual a “p” a la veinticuatro.

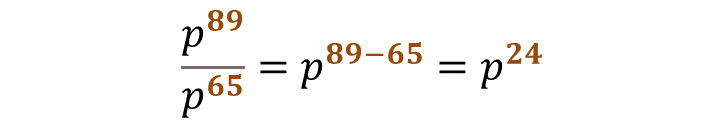
Has obtenido una generalización para el cociente de potencias de la misma base y has corroborado que la generalización aplica para cualquier base. Recapitula.

Se sabe que en un cociente de la misma base los exponentes se restan, es decir, al exponente de la potencia del numerador se le resta el exponente de la potencia del denominador y la base se conserva. Esto es: “a” a la “m” entre “a” a la “n” es igual a “a” a la “m” menos “n”. En donde “m” y “n” son números enteros.

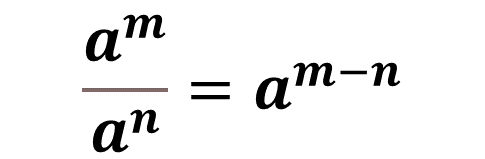
Has finalizado la sesión. Recuerda elaborar tus notas, considerando las ideas más importantes del tema que estudiaste y anota tus dudas y posibles dificultades.

Considera que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.

El reto de hoy:

Analiza y resuelve la siguiente situación:

Irma e Israel dicen que la distancia de la Tierra al Sol es aproximadamente 394 veces mayor que la distancia de la Tierra a la Luna. Ellos consideraron que la distancia de la Tierra al Sol es de 1.5 por diez a la ocho, kilómetros; y que la distancia de la Tierra a la Luna es de 3.8 por diez a la cinco, kilómetros. De acuerdo con lo estudiado, aplica la generalización e indica si Irma e Israel están en lo correcto y argumenta tu respuesta.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

Descarga tu clase dando clic aquí