Cálculo del tanto por ciento en situaciones de compra y venta II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57
Cálculo del tanto por ciento en situaciones de compra y venta II
Aprendizaje esperado: cálculo del tanto por ciento de cantidades mediante diversos procedimientos (aplicación de la correspondencia “por cada 100, n”, aplicación de una fracción común o decimal, uso de 10% como base).
Énfasis: calcular porcentajes tomando como base el cálculo de 10 por ciento.
¿Qué vamos a aprender?
Calcularás el tanto por ciento de cantidades mediante diversos procedimientos aplicando la correspondencia “por cada 100, n”, aplicación de una fracción común o decimal, uso de 10% como base.
Para explorar más sobre el tema, puedes consultar el libro de texto de Desafíos matemáticos de 6º, se explica el tema a partir de la página 37
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/37
¿Qué hacemos?
Recuerda que para calcular porcentajes, se toma como base la idea de un total que representa el cien por ciento, que puedes dividir en cien partes, y que la centésima parte es el uno por ciento de este total. Con ello podrás calcular los porcentajes de distintas cantidades, en situaciones prácticas.
Actividad 1
Ahora concéntrate en el desafío de la página 37 de tu libro de texto.
Luis, Ana y Javier venden artesanías, cada quien en su puesto del mercado. Decidieron ofrecer toda su mercancía con 10% de descuento.
Completa la tabla.
¿Cuántos puestos del mercado decidieron ofrecer su mercancía con un 10 por ciento de descuento?
Observa la tabla, ve los datos que se presentan y cuáles hacen falta para completar la actividad.
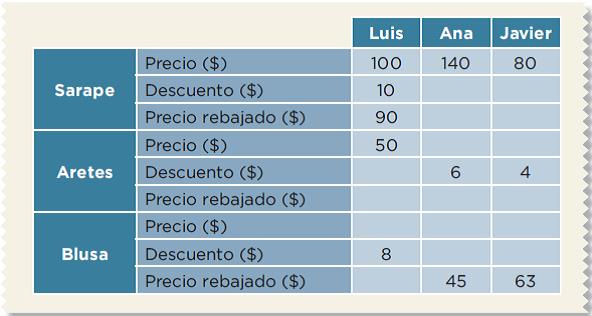
Muestra cinco columnas, tres de ellas representan las tiendas, la de Luis, Ana y Javier. Y en las filas encuentras los objetos que se venden en las tres tiendas: sarape, aretes y blusa. ¿qué datos encuentras en la segunda columna de la tabla?
Todas las cantidades que aparecen en las columnas, que tenemos que completar, expresarán cantidades en pesos.
A continuación planteamos preguntas con los datos de la tienda de Luis sobre el costo de los sarapes. De esta manera tendrás una idea más clara del tipo de información que debes anotar en cada uno de los espacios faltantes.
| Precio ($) | 100 | ¿Cuál es el precio del sarape? |
| Descuento ($) | 10 | ¿Cuánto dinero le van a descontar? |
| Precio rebajado ($) | 90 | ¿Cuánto cuesta el sarape con descuento? |
Vas a trabajar con el 10 por ciento de descuento en cada una de las mercancías que te presenta la tabla. Recuerda que el precio original de cada producto es el total a partir del cual se calcula el porcentaje de descuento. Por ejemplo, ¿cuál es el total del sarape en la tienda de Luis?
Actividad 2
Realiza los cálculos necesarios para encontrar los precios rebajados de los sarapes en las tiendas de Ana y Javier.
Observa la tabla.
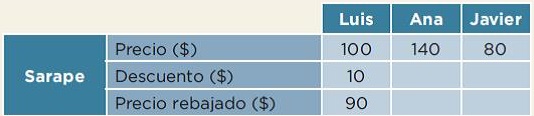
Inicia la búsqueda del precio rebajado del sarape en la tienda de Ana. El costo total del sarape de la tienda de Ana es de 140 pesos, que es lo mismo que el 100 por ciento. En la segunda fila tienes que escribir en dinero la cantidad que representa el 10 por ciento de 140 pesos, ¿cómo crees que lo puedas encontrar?
Puedo aplicar lo que hicimos con los billetes de 100 pesos en clases anteriores. El 1 por ciento de 100 pesos es un peso, por lo que el 10 por ciento son 10 pesos. De manera parecida, el 1 por ciento de 40 pesos son 40 centavos, por lo que el 10 por ciento son 4 pesos.
Por lo tanto, el 10 por ciento de 140 pesos es igual a 14 pesos. Vamos a colocarlo en la tabla.
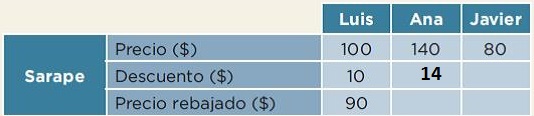
En este punto debes tener en mente que el costo con descuento es algo que se va a pagar menor al precio original del sarape. Puedes hacer una resta y colócala la respuesta.
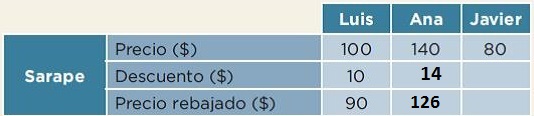
Mira el descuento y el precio del sarape que ofrece la tienda de Javier. Pero antes, te planteamos un acertijo: al observar la tabla podemos ver que el precio rebajado del sarape en la tienda de Luis es de 90 pesos y en la de Ana, 126 pesos. Claramente podemos ver cuál es más barato, ¿crees que en la tienda de Javier su precio sea menor al de la tienda de Luis?
Responde y argumenta.
El costo total del sarape es de 80 pesos, que equivale al 100 por ciento. El 1 por ciento de 80 pesos son 80 centavos y el 10 por ciento son 8 pesos.
| 100% | 1% | 10% |
| $80 | $ 0.80 | $ 8 |
Y luego, el precio rebajado lo obtenemos restando 80 pesos menos 8 pesos, lo que nos da 72 pesos.
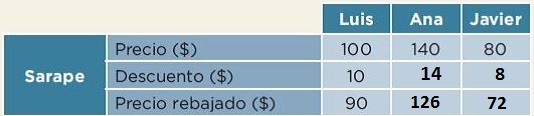
De esta manera comprobamos que el sarape en la tienda de Javier tiene el precio más barato de las tres tiendas. Así que el precio total nos dio una pista de que podía ser más barato.
Actividad 3
Realiza los calculos necesarios para conocer el precio rebajado de los aretes en las tres tiendas.
Los aretes tambien tienen un 10% de descuento, pero en este caso, la tabla te proporciona datos que están en diferente renglón.
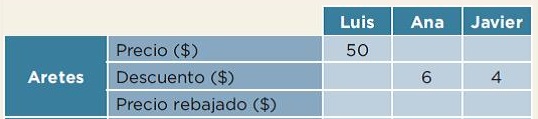
En la primera columna dice el costo total de los aretes en la tienda de Luis. ¿Qué te parece si calculas el descuento y el precio rebajado de estos aretes y luego vas a lo que sucede en la tienda de Ana y Javier?
Puedes seguir un camino un poco distinto. Si te fijas en los resultados que obtuviste con los sarapes de Ana y Javier, el 10 por ciento del precio original es igual a la décima parte del mismo, porque diez veces la centésima parte de un total es la décima parte del mismo, ¿te acuerda de la multiplicación de fracciones?
El 10 por ciento de un total es la décima parte. Entonces, el descuento de los aretes de Luis es de 5 pesos y el precio final con descuento es de 45 pesos.
10% de $50 = $5
$50 - $5 = $45
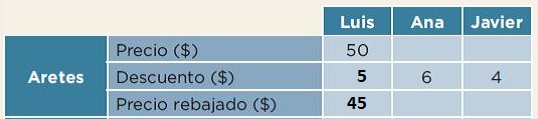
Actividad 4
Observa los datos que tienes y los que faltan sobre el costo de los aretes en las tiendas de Ana y Javier. ¿En cuál tienda piensas que están más baratos los aretes?
¿Qué harías para encontrar los otros datos, el precio total y el precio con descuento?
Recuerda el ejemplo de la señora Fernanda y sus hijos y calculaste el precio original de una chamarra, cuando conocías el descuento y el precio final, nos fue útil tomar en cuenta que si el descuento era del 10 por ciento, entonces, el precio con descuento era el 90 por ciento del precio original y que juntos sumaban el 100 por ciento.
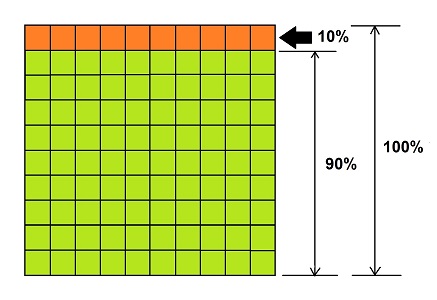
Representa estas relaciones en el siguiente cuadro:
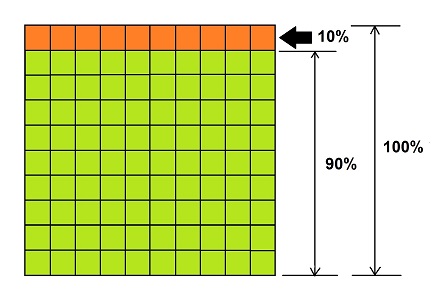
El cuadro está dividido en 100 cuadritos iguales, que juntos representan el 100 por ciento, que en este caso es el costo original de los aretes. En la fila resaltada de color naranja hay 10 cuadritos, que conforman el 10 por ciento o descuento, y la parte resaltada con verde está formada por 90 cuadritos, que representan el 90 por ciento y, que en este caso, es el precio final con descuento.
Acuérdate de la equivalencia de la información que tienes y de la que te falta respecto de los porcentajes: el precio original es el 100 por ciento; el descuento es el 10 por ciento y el precio rebajado es el 90 por ciento.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $__ | = | $6 | + | $__ |
Encuentra el precio total de los aretes sumando 10 veces el 10 por ciento o multiplicarlo por 10.
$6 X 10 = $60
Anota el resultado en la tabla.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $60 | = | $6 | + | $54 |
Ya puedes calcular el precio rebajado: son 60 pesos menos 6 pesos, lo que da 54 pesos.
Pero también lo podemos hacer de otra manera: si 6 pesos es el 10 por ciento, eso cabe 9 veces en el 90 por ciento, por lo tanto, el precio final lo podemos obtener por medio de una multiplicación. ¿Se dan cuenta de cuál es?
Sí, podemos multiplicar el descuento del 10 por ciento por nueve, para obtener el 90 por ciento! Y nueve por seis también nos da cincuentaicuatro.
Anota el resultado en la tabla.

Ahora, te falta conocer el precio original y el precio con descuento de los aretes en la tienda de Javier. Entonces, ¿te acuerdas como hacerle? Mira nuevamente tu gráfico.
El descuento es de 4 pesos, que equivale al 10 por ciento, que puedes ver como la fila en color naranja. Entonces lo multiplicas por 10 para obtener el 100 por ciento, que es el precio total, que equivale a toda el área del cuadrado. Y para obtener el precio con descuento, lo multiplicas por nueve, que es el área resaltada en color verde.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $40 | = | $4 | + | $36 |
Anota los resultados de tu cuadro.
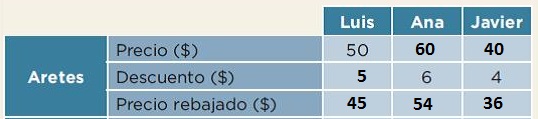
Cuando empezaste los cálculos de los aretes, pensaste que los más baratos eran los de la tiende de Ana. Con los resultados obtenidos puedes observar que los más baratos están en la tienda de Javier, ¿Qué puedes concluir de la diferencia entre lo primero que pensaste y los resultados?
Realiza el cálculo del último artículo, que es una blusa. Ve qué datos tienes.
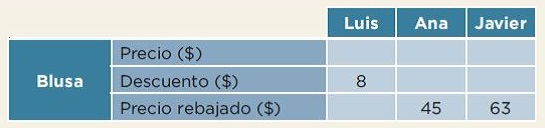
El dato de la tienda de Luis es parecido a los datos que tenías antes para los aretes en las tiendas de Ana y Javier. Entonces, puedes seguir el mismo procedimiento.
Mira nuevamente el cuadro de equivalencias para que te apoyes.
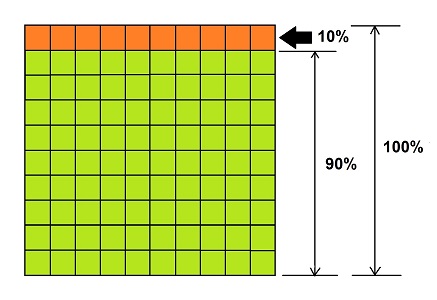
Si la blusa tiene un descuento de 8 pesos, ¿eso a cuánto equivale en el cuadro?, ¿ya lo encontraste?, ¿por cuánto tienes que multiplicar 8 pesos para obtener el precio original, es decir, el 100 por ciento?, ¿cómo puedes obtener el precio final? Recuerda que planteamos dos caminos, pero que tu puedes descubrir algún otro.
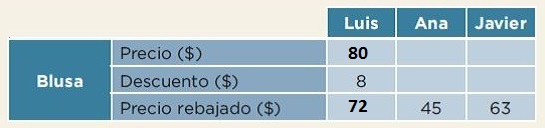
Observa las dos siguientes columnas: en la tienda de Ana y Javier tenemos el precio con descuento, pero debes obtener el precio original y el monto del descuento. ¿Cómo le puedes hacer?
Utiliza nuevamente el cuadro de equivalencias en porcentajes.
El dato que tienes en el caso de Ana es que el precio rebajado es de 45 pesos, que equivale al 90 por ciento del total; por lo que debes encontrar a cuánto equivale el 10 por ciento, que es el descuento, y el 100 por ciento, que es el precio original.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $__ | = | $__ | + | $45 |
¿Cómo le harás para encontrar los datos faltantes?
Realiza la operación y anota el resultado en tu cuadro:
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $50 | = | $5 | + | $45 |
Puedes anotar los resultados en la tabla:

El precio total de la blusa en la tienda de Ana es de $50 pesos. En los otros casos, utilizaste una resta para saber del precio original cuánto le tenías que quitar para llegar al precio rebajado o al descuento. Ahora, que tienes el precio con descuento y encontraste cuál era el monto de éste, suma estas dos cantidades para obtener el precio original.
Ve con la tienda de Javier. Ahí, una blusa con descuento cuesta 63 pesos que equivale al 90 por ciento del total; entonces, el descuento lo obtienes.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $__ | = | $__ | + | $63 |
Lo que tienes que hacer es dividir entre 9 para obtener el descuento del 10 por ciento, lo que nos da 7 pesos, y sumar las dos cantidades para llegar al precio original.
Completa la tabla y anota esos resultados en el cuadro respectivo.
| Precio original | Descuento | Precio rebajado | ||
| 100% | = | 10% | + | 90% |
| $70 | = | $7 | + | $63 |
Por último comprueba tus resultados.
El reto de hoy:
Descubre a cuánto equivale en porcentaje un grupo de cinco personas en una población de veinticinco.
Utiliza el cuadro que hiciste a lo largo de la clase: ¿cuántas filas caben 5 veces en el cuadro total?; ¿eso a qué porcentaje corresponde?
Si en tu casa hay libros relacionados con el tema, consúltalos. Así podrás saber más. Si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion