Butacas y leche

Butacas y leche

Aprendizaje esperado: exploración de distintos significados de la multiplicación (relación proporcional entre medidas, producto de medidas, combinatoria) y desarrollo de procedimientos para el cálculo mental o escrito.

Énfasis: utilizar la multiplicación para resolver problemas de proporcionalidad.

¿Qué vamos a aprender?

Aprenderás a utilizar la multiplicación para resolver problemas de proporcionalidad.

Seguramente recuerdas cuando desfilaste un 16 de septiembre o un 20 de noviembre, quizás ibas en preescolar o en los primeros grados de primaria.

Para integrarse al desfile de una manera ordenada, ¿Cómo se acomodaban al formar un contingente? seguramente por filas o hileras.

¿Cómo se podrían acomodar 30 niñas y niños para desfilar, sin que nadie sobrara?

Para resolver esta situación se requiere encontrar una multiplicación que dé como resultado 30 y así encontrar el número de filas a colocar, por ejemplo:

Entonces, se pueden formar 5 filas de 6 integrantes o 6 filas de 5 integrantes.

¿Y si fueran 32 niñas y niños? puedes optar por formar 4 filas de 8 u 8 filas de 4, porque .

Debes considerar que hay más formas de organizar a los alumnos como 2 filas de 16 alumnos, por ejemplo.

¿Y si fueran 43 niñas y niños? ¡Sobraría 1! porque , y se podrían formar 6 filas de 7 o 7 hileras de 6.

Así se estaría formando un contingente proporcional, que justo ese es el tema que verás el día de hoy.

Esta actividad, te permitirá continuar con el trabajo de la sesión del día de hoy.

Si tienes libros en casa o cuentas con Internet, explóralos para saber más.

¿Qué hacemos?

Resuelve el siguiente problema:

Antes de resolverlo piensa, ¿Qué datos tienes? ¿Qué pregunta el problema? ¿Qué operación debes realizar para solucionar el problema?

Una vez identificados los datos, lo que pide el problema y la operación a realizar, encuentra una solución, para ello organiza la información que analizaste:

Ahora resuelve la multiplicación:

• En este problema vas a multiplicar el número de filas, en este caso 4, por el total de botellas que lleva cada fila, que es 30.
• Empieza por las unidades, primero multiplicas 4 por cero, da 0. Recuerda que todo número multiplicado por 0 da 0, y lo anotas como primer dígito del producto.
• Posteriormente haces lo mismo con las decenas, o sea ; se coloca como complemento del resultado y listo, tienes la operación completada, con un total de 120.

Representado en el esquema queda de la siguiente manera:

Se puede notar que el resultado pasa a responder la pregunta que planteó el problema, puedes decir que en este problema van acomodadas las botellas en un gran contingente de 120.

Resuelve el siguiente problema:

Organiza tu información.

Ahora da solución a la multiplicación que te ayudará a resolver el problema.

Como ves, se debe multiplicar el número total de sacos, 385, por el peso de un saco, en este caso 8kg.

• Primero multiplicas el 8 por las unidades, en este caso el 5, que da por resultado 40 sólo anotas en el resultado el 0 debajo, alineado a las unidades y llevas el 4 encima del 8, de las decenas, en el multiplicador.
• Enseguida multiplicas 8 por 8, que da 64 a ese resultado le sumas 4 que llevas y da 68, por lo que anotas 8 en el producto, en la columna de las decenas y el 6 lo llevas encima de las 3 centenas del multiplicador.
• Por último, multiplicas 8 por 3, que da 24, pero le sumas los 6 que llevas y da 30 esa cantidad la anotas en el producto para completar la operación ¡Y ya queda la operación resuelta!

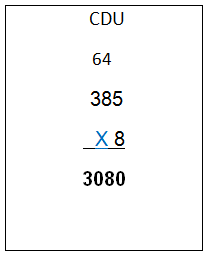
Observa que al anotar el resultado le agregas "kilogramos”.

Resuelve el siguiente problema:

Para resolver este problema de magnitudes proporcionales, el método de valor unitario puede ser muy útil, se desarrolla de la siguiente manera:

• Se trata de descubrir cuál es el valor de una de las magnitudes cuando la otra vale 1, cuando es la unidad.
• En esta situación las magnitudes son: Cantidad de latas y Precio.
• Para establecer el valor unitario, solo tienes que preguntar ¿Cuánto costaría 1 lata?

Para saberlo, puedes hacer varios procedimientos.

APOYARTE EN UNA TABLA DE VARIACIÓN, que es un organizador gráfico en el que acomodas los datos conocidos del problema y vas analizando qué sucede con las magnitudes cuando las aumentas o disminuyes ¿Qué datos conoces del problema?

8 latas de frutas en conserva cuestan $ 280.00

Coloca esa información en tu tabla:

Como puedes observar, es una tabla con 8 renglones, uno por cada cantidad de latas y un espacio que corresponde al costo de esa cantidad.

Ahora, si piensas en la mitad de la cantidad de latas, ¿Dónde colocarías el número 4? Justo a la mitad del organizador ¿Cuál sería el costo de esas latas? pues también la mitad del precio original.

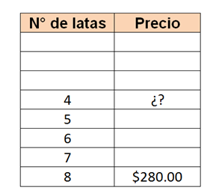
Esa es la idea central de la proporción: Una relación que se establece entre dos cantidades por lo que, si una de las magnitudes se multiplica, la otra se multiplicará de la misma manera y si se fracciona, la otra también se va a fraccionar, como en este ejemplo, a la mitad, entonces el costo de la mitad de las latas será la mitad de la cantidad.

Si sigues aplicando el mismo razonamiento, ¿Qué cantidad será la mitad de 8 latas y cuál sería su costo? la mitad de las latas es cuatro y el costo será la mitad de $ 140.00

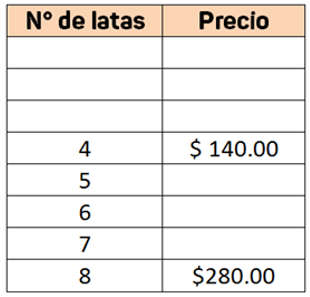
Y si obtienes la mitad de cuatro latas:

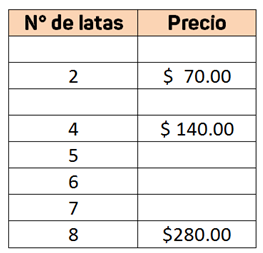
Recuerda que identificar el valor unitario significa conocer la relación que existe entre las dos cantidades, cuando una de ellas es igual a 1, en este caso, buscar el precio de 1 lata de conservas.

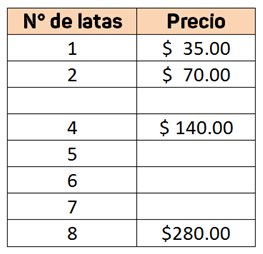
Con esta información ya puedes calcular cualquier precio de cualquier cantidad de latas.

Para conocer el precio de cualquier cantidad de latas, debes multiplicar el precio de una lata por la cantidad de latas que se quieran comprar, esta es una ventaja de conocer el valor unitario, ya que una vez que lo conoces, lo puedes aplicar para una cantidad importante de cálculos.

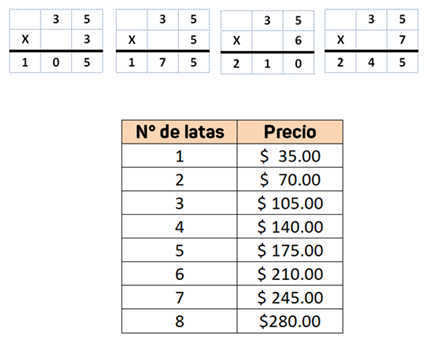
Otra forma de calcular el valor unitario es dividir el precio, $280.00 entre 8, ya que esa es la cantidad de latas que corresponde a esa cantidad, así se tiene que:

En este caso , por lo que 1 lata cuesta $ 35.00 ¡Has calculado el valor unitario de una lata!

Entonces ya puedes calcular cuánto costaría cualquier cantidad de latas de frutas en conserva: 15, 20, o incluso 1 000 latas.

Ahora, sólo tienes que multiplicar el precio de 1 unidad, $35.00, por la cantidad de unidades que desees saber.

Por ejemplo, si se pregunta por el precio de 10 latas, multiplicas y da 350 ¡Ya tienes la respuesta! ¡10 latas de frutas en conserva cuestan $ 350.00!

Resuelve el siguiente problema:

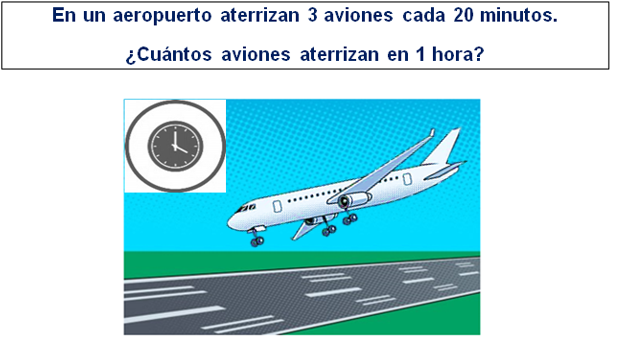
Al analizar los datos y lo que pide el problema, pareciera algo complicado de saber, pero vas a ver que no. Analiza:

• Se tienen tres aviones que aterrizan cada cierto tiempo, en este caso cada 20 minutos, entonces piensa, ¿Cuántos aviones aterrizarán en el doble de tiempo? es decir, en los siguientes 40 minutos.
• Serán 6 aviones, porque como es el doble de tiempo, sería igual o proporcional también el doble de aviones que aterricen.
• Si posteriormente a esos 40 minutos, vienen los otros 20 minutos y otros tres aviones aterrizan, ¿Cuántos aviones en total aterrizarán en 60 minutos, que es igual a una hora? serán 9 aviones; solo se suman los 3 aviones de los 20 minutos finales, a los 6 que tenías de los 40 minutos anteriores.

Observa la siguiente forma de presentar los datos del problema y así visualizar rápidamente los resultados.

Otra manera de presentar la información sería registrando los datos involucrados en la solución del problema.

Recuerda que a este organizador o tabla se le conoce con el nombre de tabla de proporcionalidad, en ella se muestra la relación de proporcionalidad entre 2 magnitudes, la cual implica que cuando una suba de valor la otra magnitud también subirá con el mismo cuantificador multiplicativo: Al doble, al triple, al cuádruple, etc., y cuando una baje su valor, la otra también lo hará a la mitad, a la tercera parte, a la cuarta parte, ambas magnitudes de la misma forma.

En este caso si aumenta el número de aviones que aterrizan, también aumentará el tiempo transcurrido entre un grupo de aterrizajes y otro.

Es decir, si se multiplica:

, aviones.

Lo tienes que hacer de igual manera en el tiempo.

, .

Así es como da 6 aviones y 40 minutos como resultado.

Y luego, para obtener el tercer valor en la tabla, se puede:

• Considerar que en una hora hay 3 periodos de 20 minutos, entonces multiplicas:
  , es decir aviones
  , es decir .
  Donde obtienes 9 aviones y 60 minutos respectivamente como resultados.
• También puedes emplear la información que vas calculando, para obtener los datos que necesitas; así que, si 3 aviones emplean 20 minutos para aterrizar, el doble de aviones, es decir 6, emplearán también el doble de tiempo, es decir 40 minutos. Si analizas, 3 aviones más 6 aviones dan por resultado 9 aviones, que es la información que buscas. Por lo anterior, puedes sumar también los tiempos que emplean 3 y 6 aviones para aterrizar, es decir, 20 minutos + 40 minutos, lo que da por resultado 60 minutos; siendo la respuesta a la pregunta: ¿Cuántos aviones aterrizan en 1 hora? 9 aviones.

Recuerda si multiplicas un valor o magnitud por 2 el otro también se multiplica por 2, porque si lo multiplicas por otro número estarías cayendo en un error.

Al aplicar la proporcionalidad, debes emplear los mismos procesos multiplicativos a las magnitudes entre las que estableces una relación numérica: Doble, triple, cuádruple, quíntuple, etc. O partitivos: Mitad, tercera parte, cuarta parte, quinta parte, etc.

Resuelve el siguiente problema:

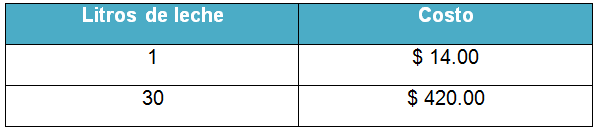
¿Cómo puedes darle solución? ¿Necesitas calcular el valor unitario del litro de leche? En este caso no necesitas calcular el valor unitario del litro de leche, ya que en los datos del problema se da.

Recuerda que el valor unitario es la relación de valor que se establece entre 2 magnitudes cuando una de ellas vale 1, de manera que si ya sabes que un litro de leche cuesta $14.00, lo que queda es realizar una operación para saber cuánto costarán los 30.

En este caso vas a multiplicar los 30 litros por el precio unitario de uno de ellos, en este caso $ 14.00

Primero multiplicas el , recuerda que al multiplicar por cero, el resultado es 0. Anotas cero como primera cifra del primer producto parcial, luego multiplicas , que da 12, por lo que colocas el 2 en la columna de las centenas y el 1 pasa a la posición de las centenas. Considerando que no hay otra cifra con la cual sumarla, se coloca el 1 como la cifra con la que se concluye la primera parte de la operación.

Ahora multiplicas las decenas del multiplicador, , que da cero, lo anotas como primera cifra del segundo producto parcial y, para concluir, registras el 3, ya que realizas la sumatoria y ¡Listo! obtienes la respuesta al problema.

También puedes representar en una tabla la solución, de la siguiente forma:

Analiza el siguiente problema.

¿Cómo puedes darle solución? ¿Será útil saber cuál es el valor unitario de cuántos kilogramos come un tigre? ¿O podrás emplear una tabla de proporcionalidad y hacer las multiplicaciones correspondientes hasta obtener el resultado?

Intenta la opción de emplear la tabla de proporcionalidad, e ir aplicando proporciones.

Inicia tu tabla anotando en una columna los números de tigres y en la otra el de kilogramos de carne que consumen:

Realiza las multiplicaciones con ambos datos, recuerda que, si multiplicas por un número la primera cantidad, al igual lo harás por el mismo número con la otra cantidad:

, ahora ya tienes 6 tigres.

, ahora ya tienes 80 kilogramos de carne.

Lo anotas en la tabla.

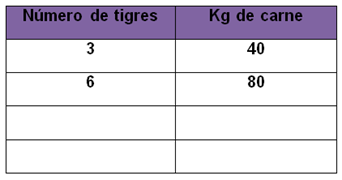
Sigue realizando las multiplicaciones.

ahora ya tienes 9 tigres.

ahora ya tenemos 120 kilogramos de carne.

Lo anotas en tu tabla.

Continúa:

ahora ya tienes 12 tigres.

ahora ya tenemos 160 kg de carne.

Lo anotas en tu tabla.

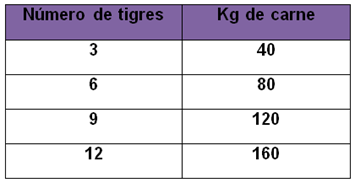
Como puedes darte cuenta, hasta ahí quedaría la tabla ya que has obtenido la cantidad de carne que necesitas para alimentar a los doce tigres ¡Listo! has solucionado el problema.

Analiza y resuelve el siguiente problema:

Reflexiona, ¿Qué hacer para ir solucionando el problema? Primeramente, realiza una suma mental de los 600 alumnos más los 45 maestros son 645 personas, ahora, ¿Qué operación es conveniente realizar?

Tienes que multiplicar la cantidad de filas, en este caso 27, por el total de asientos que hay en cada fila, que en este caso son 24.

Primero se multiplica el 4 por el 7, , se anota el 8 como primera cifra del producto parcial y las 2 decenas se colocan en la posición que corresponde, que es el 2 que está junto al 7.

Posteriormente más los 2 que llevas, da 10 y se anota a la derecha del 8 en el primer producto parcial, quedando de la siguiente manera.

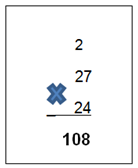
Ahora multiplicas la siguiente cifra del multiplicador que es el dos y que está a la derecha del 4, de manera que anotas el 4 debajo de la posición de las decenas que ocupa también el 0, respetando el orden de la multiplicación, y llevas la centena obtenida a la siguiente posición a la izquierda, 1 lo puedes mantener en tu mente, enseguida multiplicas más la unidad que llevas son 5 y lo anotas debajo del 1, quedando de la siguiente manera:

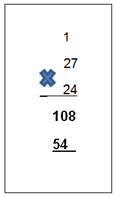
Por último, haces la suma de los productos parciales, obteniendo:

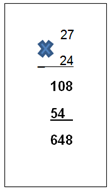
Y ¡Listo! obtienes el total de asientos del cine.

Ahora, ¿Qué necesitas hacer para saber si alcanzan a entrar todos los alumnos y maestros en el cine? muy fácil, compara la cantidad total de alumnos y la cantidad de asientos con los que cuenta el cine, tenemos que en total tiene 648 lugares disponibles y son 645 personas, por lo tanto, sí alcanzan y sobran 3 lugares.

Como puedes darte cuenta, el emplear la multiplicación en los problemas de proporcionalidad te permite llegar a obtener el resultado de una manera rápida y eficiente, pero para ello es indispensable que repases las tablas de multiplicar.

El día de hoy has aprendido a utilizar la multiplicación y resolver problemas de proporcionalidad.

El reto de hoy:

Resuelve el primer problema de la página 30 de tu libro de Desafíos matemáticos.

Recuerda que debes comentar el reto con tu maestra o maestro para analizar sus resultados.

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/