Área de figuras compuestas

Área de figuras compuestas

Aprendizaje esperado: calcula perímetros de polígonos y círculos, así como áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.

Énfasis: calcular el área de figuras compuestas (descomposición en figuras conocidas); aplicar las fórmulas correspondientes.

¿Qué vamos a aprender?

En esta sesión calcularás el área de figuras compuestas, aplicando los conocimientos adquiridos sobre las fórmulas del área de triángulos y cuadriláteros.

Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, regla y tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas Leyer, un punzón y una regleta.

¿Qué hacemos?

Para iniciar se resolverá una situación que tiene una compañera tuya llamada Sofía, que se dio a la tarea de elaborar con materiales de rehúso una caja muy original y que servirá para enviarle un regalo a su abuelo, esta caja tiene forma de prisma triangular y desea forrarla del color preferido de su abuelo, el amarillo. Ella se dio a la tarea de investigar y encontró que en una papelería venden cierto tipo de papel por metro cuadrado, pero no sabe realmente qué cantidad comprar, ya que desea, desperdiciar la menor cantidad de papel posible.

¿Qué estrategia emplearías para calcular la cantidad de papel que se necesita para forrar la caja de manera que se desperdicie lo menos posible?

En este caso, lo que tienes que hacer es calcular el área total de las caras del prisma, para así calcular la cantidad de papel que se necesita. Es importante aclarar que se calculará el área de las caras, no el volumen del prisma.

Para obtener las medidas necesitas conocer las medidas de la base y altura del prisma, para ello, se puede decir que los triángulos de la base son triángulos rectángulos, hay que ver cuánto miden sus lados.

Miden 20 cm, 25 cm y 32 cm, pero vas a considerar el lado de 20 cm como la base y el de 25 cm representa la altura.

Ya puedes calcular el área de las bases del prisma. Como sabes, para calcular el área de un triángulo debes multiplicar la medida de la base por la altura y posteriormente este resultado se divide entre dos.

Se te recuerda que la fórmula es muy parecida a la fórmula que se utiliza para calcular el área de un rectángulo y únicamente agregas la división entre dos ya que de un rectángulo puedes obtener dos triángulos congruentes entre sí.

Continuando, para calcular el área del triángulo, multiplicas 20 por 25, lo que te da como resultado 500, este número lo divides entre 2 y el resultado final es 250, que representa el área del triángulo de la base del prisma, en centímetros cuadrados.

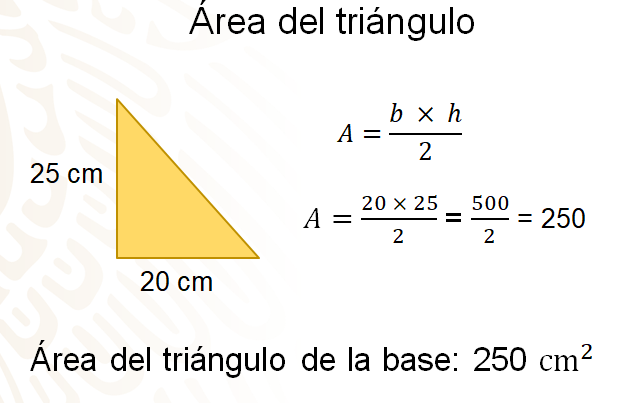
Ya tienes el área de una de las bases, ahora sólo debes duplicar este resultado ya que el prisma tiene 2 bases que son iguales. ¿Lo tienes?

Si el área total de una base es 250 centímetros cuadrados, entonces el área total de las dos bases es de 500 centímetro cuadrados.

¿Qué área te falta calcular?

El área de las caras laterales de la caja, ¿puedes mencionar qué forma tienen?

Son rectángulos y para calcular su área, ya conoces una de sus medidas, y será necesario conocer la altura del prisma, para conocer la otra. Entonces hay que medirla.

El prisma tiene una altura de 30 centímetros.

Tienes 30 centímetros exactamente en la altura de la caja. Ahora hay que comenzar calculando el área de una de las caras de uno de los rectángulos o bien, la cara lateral del prisma, que mide 20 centímetros en la base, y 30 centímetros de altura.

Aplicas la fórmula para calcular el área del rectángulo, la cual es base, por altura. Así, veinte por treinta es igual a 600 centímetros cuadrados.

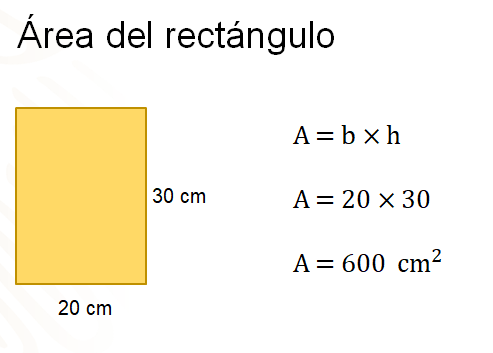
Ya tienes el área de esta cara lateral, ¿con cuál cara continuarás?

La siguiente cara mide 25 centímetros de base por 30 centímetros de altura.

Utilizas de nuevo la fórmula base por altura, y multiplicas 25 por 30, de esta manera obtienes que el área de esta cara es de 750 centímetros cuadrados.

Ahora, sólo te falta calcular la medida de una cara lateral, tienes 32 cm de base y 30 centímetros de la altura que ya conoces.

Tienes la fórmula base por altura, sustituyes los valores que ya conoces en la fórmula y de esa manera tienes el producto de 32 por 30, que es 960 centímetros cuadrados.

Ya tienes el área de las bases y el área de las caras laterales del prisma. Ahora, ¿qué debes hacer?

Debes sumar todas las áreas para saber cuál es el área total de las caras de la caja y luego hacer los cálculos para conocer la cantidad de papel que se debe comprar.

Recapitulando, el área de ambas bases del prisma es de 500 centímetros cuadrados, la cara lateral 1 tiene un área de 600 centímetros cuadrados, la 2 de 750 y la cara lateral 3 tiene un área de 960 centímetros cuadrados.

Sumas las 4 cantidades y obtienes que el área total de las caras del prisma es de 2 810 centímetros cuadrados. Ahora debes calcular la cantidad de papel que se necesita, piensa ¿qué características tiene?

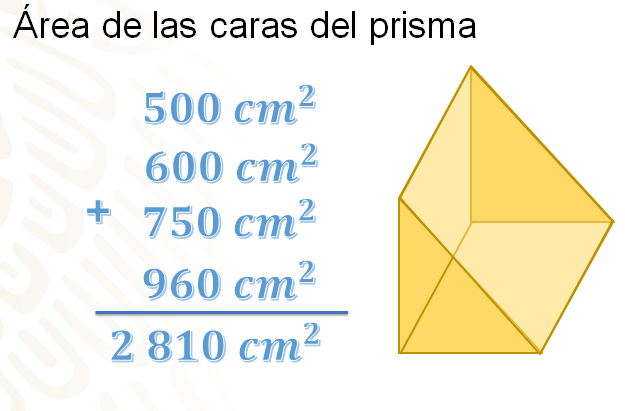
Sofía dice que le comentó el encargado, que el papel que le agradó mide de ancho 35 centímetros, y puede venderle la cantidad de papel que necesite. Así que necesita un área total de papel de 2 810 centímetros cuadrados, ¿qué estrategia se puede utilizar para conocer la longitud de papel que debe solicitar Sofía?

Ten en mente que lo que comprará Sofía, será un rectángulo de papel y éste debe tener de área de 2810 centímetros cuadrados, como mínimo, el ancho de este rectángulo es de 35 centímetros. Por lo tanto, ¿cuánto debe medir su largo?

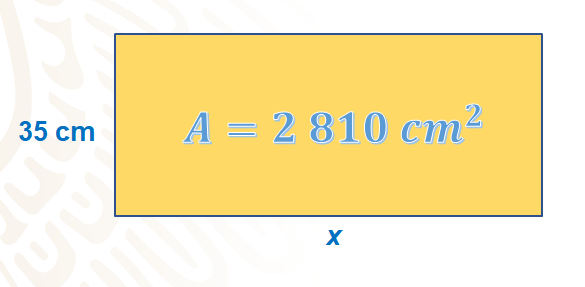
Seguramente ya sabes que hacer y puedes sugerir la cantidad de papel que debe comprar Sofía. En este sentido, ¿qué estrategia empleaste para saber cuánto mide el largo del rectángulo?

Así es, la división del área entre la longitud que ya conoces te dará la cantidad de papel que debe solicitar Sofía al encargado de la papelería.

Pues, 2810 entre 35 da como resultado 80.2, ese es el largo de papel que debe solicitar Sofía al empleado para cubrir las superficies de la caja que servirá como envoltura del regalo que se le hará al abuelo. Para hacerlo más sencillo, le solicitará 85 centímetros de papel.

Para seguir profundizando en tus conocimientos sobre el cálculo de áreas, revisa la siguiente situación.

La imagen que se te mostrará a continuación aparece en la pared del patio central de una escuela, como la pintura ya se desgasto, tienen que volver a pintarla. La persona que realizará el trabajo necesita medir la superficie para saber cuánto tiene que cobrar.

La figura es una casa formada por diferentes figuras geométricas: uno es un rectángulo que mide de base 2 metros y de altura 1.3 metros, la figura 2 es un triángulo que mide de altura 120 centímetros; la figura 3 es un romboide en el que su base mide 250 centímetros y la figura cuatro es otro rectángulo que mide de base lo que el romboide, 250 centímetros y de altura, mide lo mismo que el otro rectángulo, 1.3 metros.

Comenzando con la figura 1, usa la fórmula que ya recordaste anteriormente la cual dice que debes multiplicar la longitud de la base por la de la altura, es decir, 2 por 1.3, el resultado es 2.6 metros cuadrados.

Para la figura 2, usarás la fórmula base por altura entre 2, como puedes notar en la imagen, la medida de la base del triángulo es equivalente a la medida de la base de la figura 1, es decir, 2 metros, y la altura mide en total 120 centímetros. Para realizar los cálculos debes utilizar la misma unidad de medida, por lo tanto, tomarás como la medida de la base 2 metros, posteriormente debes multiplicar este número por 1.2 que es el equivalente en metros de 120 centímetros y después lo dividirás entre dos; el resultado del producto es 2.4 y el resultado de este número dividido entre 2 es igual a 1.2 metros cuadrados.

Para la figura 3, ocuparás la misma fórmula que para el rectángulo ya que como has visto con anterioridad la superficie que ocupa cierto romboide, será equivalente a la superficie que ocupe un rectángulo con la misma medida en la base y en la altura. La medida de la base de este romboide es 250 centímetros, o bien 2.5 metros y la altura es la misma que la del triángulo,1.2 metros, haces los cálculos correspondientes y tienes que el producto es 3 metros cuadrados.

Para la figura 4 multiplicarás de nuevo la base por la altura, es decir, 2.5 por 1.3 de lo que te resulta 3.25 metros cuadrados.

Por último, debes sumar los resultados que obtuviste ya que el objetivo es calcular el total de la superficie que ocupa la pintura, 2.6 más 1.2, más 3, más 3.25 es igual a 10.05 metros cuadrados de superficie.

Ahora, se te presentará una figura diferente, en la que debes calcular el área de la parte sombreada, analízala cuidadosamente.

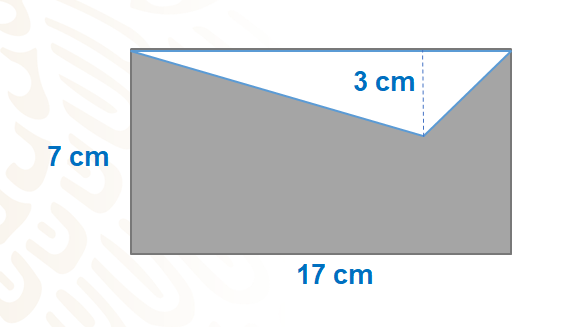
¿Qué debes hacer para calcular el área de la parte sombreada?

Debes calcular el área del rectángulo que puedes ver y cuyas longitudes son, base, posteriormente sacar el área del triángulo y por último debes calcular la diferencia entre ambas. De este modo obtendrás únicamente la medida de la superficie de la parte sombreada.

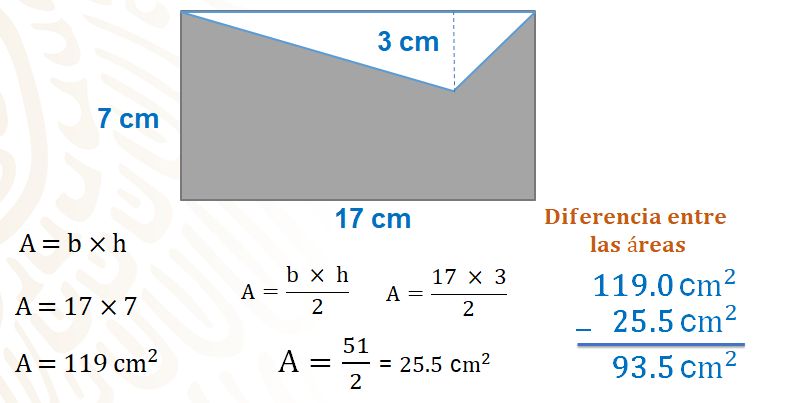
Aplica la fórmula base por altura, multiplica 17 por 7, el resultado es 119 centímetros cuadrados, que corresponde al área del rectángulo.

Ahora trabaja con el triángulo, la fórmula para sacar el área de un triángulo es base por altura entre dos. Puedes tomar la misma longitud de la base del rectángulo para la base del triángulo, es decir, 17 centímetros y la altura es de 3 centímetros; el producto de estos dos números es 51 y al dividir entre 2, obtienes como resultado 25.5 centímetros cuadrados.

Saca la diferencia entre estos dos números, al área del rectángulo, le restas el área del triángulo, 119 menos 25.5 da como resultado 93.5 centímetros cuadrados del área sombreada.

Para aplicarlo a tus conocimientos sobre el cálculo de áreas, revisa el siguiente audiovisual que trata sobre el tema.

• El área de polígonos.
  https://www.youtube.com/watch?v=6HIADlG1mQc
  Revisa del tiempo 00:37 al 02:33.
  Ahora, hay que resolver el problema empleando la segunda imagen presentada en el video. Recuerda que se trata de un terreno, y para poder conocer su área total, es necesario seccionarlo en figuras como son triángulos y cuadriláteros, cuyas fórmulas para calcular su área ya conoces. Hay que realizar los cálculos.
  Recuerda que, la imagen que representa el terreno ya está dividida en unidades cuadradas, por lo tanto, para conocer las longitudes de los lotes, únicamente debes contarlas, por ejemplo, la figura A es un triángulo que mide de base 10 metros, y de altura 2; la figura B es un rectángulo cuya base mide 7 metros y de altura 8; la figura C es un triángulo, tomarás como base el lado que mide 4 metros y la altura mide 3. El triángulo de la figura C mide de base 3 metros y de altura 4, como puedes ver es igual al anterior, el rectángulo de la figura E mide 3 metros de base y 4 metros de altura; la figura F es un triángulo que mide de base 1 metro y de altura 4 metros.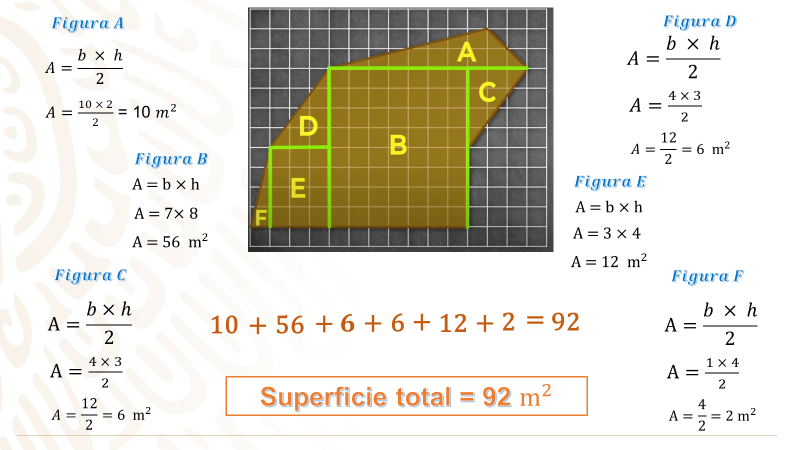
  
  Comenzando con el lote A, usarás la fórmula base por altura entre 2, multiplicas 10 por 2 y después divides entre 2, aquí se menciona que puedes ahorrarte la multiplicación por dos y la división entre dos, ya que, al ser operaciones contrarias por el mismo número, el resultado será el mismo, en este caso 10 ya que este número primero se duplica y luego se divide a la mitad, así que con este razonamiento puedes llegar al resultado que es 10.
  Para el lote B, usas la fórmula base por altura, el producto de 7 por 8 es 56, esa es el área del lote B.
  La figura C es otro triángulo, al multiplicar la longitud de su base por la longitud de su altura, obtienes como resultado 12 y este número entre 2, te da como resultado que el área de este lote es de sólo 6 metros cuadrados.
  Para el triángulo de la figura D, no será necesario realizar los cálculos de nuevo, ya que es igual al lote C; por lo tanto, su área es de 6 metros cuadrados.
  El rectángulo del lote E mide 3 por 4; por lo tanto, su área es de 12 metros cuadrados.
  Por último, el área del triángulo que mide un metro de base por 4 de altura y que pertenece al lote F, mide en total, 2 metros cuadrados.
  Ahora, se suman estos 6 resultados, como puedes ver, el resultado es el mismo al que se mostró en el audiovisual, es decir, la superficie total del terreno es de 92 metros cuadrados.
  Ya has resuelto varias actividades en las que has tenido que calcular el área de figuras compuestas por triángulos y cuadriláteros, y otras figuras irregulares, como pudiste ver, en todos los casos la estrategia que se ha seguido es descomponer la figura en otras, de manera que sea posible aplicar las fórmulas que ya conoces bien, sólo debes tener cuidado en establecer las medidas correctas, en el caso de que no cuentes con ellas a simple vista, y al final, debes sumar todas las áreas obtenidas para obtener la medida de la superficie que se busca.
  Como has podido comprobar una vez más, las matemáticas se encuentran a tu alrededor, se te invita de nuevo a que pienses en una situación similar e identifiques figuras irregulares que puedan dividirse en triángulos y cuadriláteros, piensa en la manera de dividir las figuras de manera que te sea posible calcular su área, verás que puedes divertirte. Cuando trabajes con las fórmulas, recuerda la estrecha relación que hay entre ellas.
  Continúa estudiando, esfuérzate y lograrás tus objetivos.
  El reto de hoy:
  Con la información que revisaste en este tema, responde la siguiente pregunta:
• ¿Se te ocurre alguna situación en la que tengas que hacer uso del cálculo de áreas de figuras compuestas?

Asimismo, concluye tus ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html