Aplicar las reglas de los signos para la multiplicación y división de números decimales positivos y negativos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06Aprendizaje esperado: resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos.
Énfasis: aplicar las Leyes de los signos para la multiplicación y división de números decimales con signo positivo y negativo.
¿Qué vamos a aprender?
Continuarás con el estudio de la multiplicación y división con números decimales positivos y negativos, y profundizarás en cómo usar las reglas de los signos para la resolución de problemas dentro de su contexto.
¿Qué hacemos?
Para iniciar esta sesión, observa el siguiente video, analiza la multiplicación y la división con números decimales positivos y negativos. Este video te ayudará a recordar la manera de utilizar y representar los números decimales.
La historia de las fracciones y los números decimales.
https://www.youtube.com/watch?v=NEPaQ1ae5Rs
Después de que viste el video, realiza la siguiente actividad.
Escribe los siguientes números como decimal en tu cuaderno.
Por ejemplo: cuatro enteros dos décimos, (la respuesta es: 4.2).
- Seis décimos
- Trece enteros cinco décimos
- Veintidós enteros cinco centésimos
- Ocho enteros cinco milésimos.
Ahora, reflexionarás sobre el uso de los números decimales en la multiplicación. Observa el siguiente video para recordar el procedimiento de la multiplicación con números decimales.
Algoritmo de la multiplicación con números decimales.
https://www.youtube.com/watch?v=ci1CtwX2R78
En la multiplicación de números decimales positivos y negativos se utiliza el mismo procedimiento aritmético que observaste en el video, y de la misma manera se aplican las reglas de los signos.
Observa los siguientes ejemplos, de algunas multiplicaciones de números decimales positivos y negativos.
(positivo) (positivo) = Positivo (0.3) (0.5) = 0.15
(negativo) (negativo) = Positivo (-0.3) (-0.5) = 0.15
(positivo) (negativo) = Negativo (0.3) (-0.5) = -0.15
(negativo) (positivo) = Negativo (-0.3) (0.5) = -0.15
A continuación, resuelve un problema de aplicación de la multiplicación de números decimales positivos y negativos.
Citlalli solicitó un préstamo de $4 500 en el banco, el cual tiene que pagar en 12 mensualidades fijas de $543.75
¿Cuánto pagará Citlalli en total al Banco?
¿Con qué tipo de números se pueden representar las cantidades del problema?
¿Por qué?
Préstamo: $4,500
12 mensualidades fijas de: $543.75
Por representar una deuda para Citlalli o un saldo en contra, las cantidades se representan como números negativos, es decir:
–$4 500 y –$543.75
Ahora, opera con números positivos y negativos para saber lo que tiene que pagar Citlalli al banco, es decir, para conocer su deuda.
Se plantea la operación aritmética:
(12) (-543.75) = -6525.00
Se multiplican los doce meses por la mensualidad de quinientos cuarenta y tres con setenta y cinco centavos (negativo).
De modo que la deuda de Citlalli es de –$6,525 (negativo).
Ahora resuelve la siguiente cuestión, no olvides anotar el ejercicio, así como todas las operaciones que realices.
¿Cuánto va a pagar de intereses Citlalli?
Analiza la siguiente información para recordar cómo resolver divisiones que involucran números decimales.
En general, al resolver divisiones con números decimales, se convierten a divisiones equivalentes, de manera que en el divisor quede un número entero.
Observa los tres diferentes casos.



(positivo) entre (positivo) = Positivo (0.3) ÷ (0.5) = 0.6
(negativo) entre (negativo) = Positivo (-0.3) ÷ (-0.5) = 0.6
(positivo) entre (negativo) = -Negativo (0.3) ÷ (-0.5) = -0.6
(negativo) entre (positivo) = -Negativo (-0.3) ÷ (0.5) = -0.6
Después de comprender cómo resolver divisiones que involucran números decimales positivos y negativos, resuelve el siguiente problema.
Carlos viaja a 12.75m/s en su bicicleta, aplica el freno y tarda en detenerse 8.25 segundos.
¿Cuál es el valor de la aceleración?
¿Por qué la velocidad final es cero?
La fórmula de la aceleración está definida de la siguiente manera:
Donde:
a: aceleración
: Velocidad Final =0 m/s
: Velocidad Inicial = 12.75 m/s
t: tiempo = 8.25s
Ahora se sustituyen las literales por los valores antes indicados.
Desarrollando las operaciones se tiene que:
El cociente es un número decimal periódico de dos cifras, por lo tanto, se interpreta de la siguiente manera.
La aceleración se mide en metros sobre segundo al cuadrado:
La razón por la cual aparece la unidad del tiempo elevada al cuadrado en la unidad de aceleración es debido a que la aceleración representa la variación de la velocidad por unidad de tiempo.
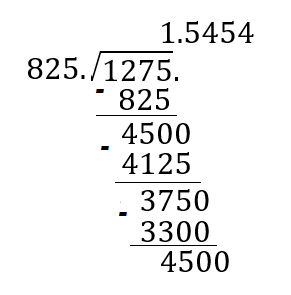
¿Por qué la aceleración es negativa?
Porque disminuyó la velocidad para detenerse, es decir desaceleró.
A continuación, vas a operar con números positivos y negativos, con otro ejemplo:
Tere vio unos zapatos con el 25% de descuento. Los zapatos cuestan $580. ¿Cuánto pagará por ellos al aplicar el descuento?
Planteamiento del problema:
¿Con qué signo se representa el porcentaje? ¿Por qué?
Negativo, porque representa el descuento del producto.
¿Cuál es la razón y el número decimal del porcentaje?
Dividiendo número negativo entre número positivo se obtiene un número negativo.
Plantea la expresión aritmética que te lleve a obtener el descuento que se aplicará al producto:
(580.00) (-0.25) =
Quinientos ochenta por veinticinco centésimos negativo donde:
- Los quinientos ochenta es el precio total de los zapatos, es decir el 100%.
- Los veinticinco centésimos negativos, son el cociente de la razón, es decir el veinticinco por ciento de descuento que se hará al precio total de los zapatos.
- Los ciento cuarenta y cinco negativos representan el descuento al precio total de los zapatos
(580.00) (-0.25) = -145.00
Plantea la expresión aritmética que represente ¿cuánto pagará Tere por los zapatos?
580.00 - 145.00 = 435.00
El pago que hará por los zapatos con el 25% de descuento es de cuatrocientos treinta y cinco pesos.
Una vez visto todo lo anterior y habiendo analizado varias situaciones. Ahora, resuelve el siguiente cuadrado mágico con números positivos y negativos.
Observa cómo resolverlo:


Ahora, analiza la siguiente imagen y responde los siguientes ejercicios:
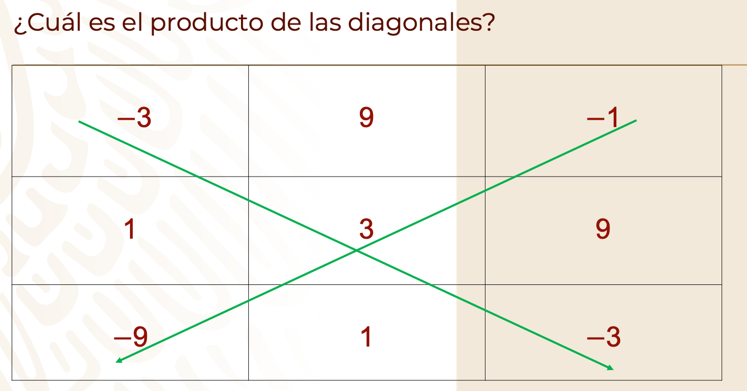
¿Cuál es el producto de las diagonales?
(-3) (3) (-3) =
(-9) (3) (-1) =
¿Cuál es el producto de las filas?
(-3) (9) (-1) =
(3) (9) =
(-9) (1) (-3) =
¿Cuál es el producto de las columnas?
(-3) (1) (-9)=
(9) (3) (1) =
(-1) (9) (-3) =
Finalmente, observa la siguiente actividad, para posteriormente realizarla.

Una vez que hayas analizado y comprendido como realizarla. Realiza el siguiente ejercicio (similar al anterior).

En esta sesión, se desarrolló el cálculo aritmético de la multiplicación y división de números decimales aplicando la regla de los signos dando solución a los ejercicios planteados.
No olvides que es necesario analizar el algoritmo de la multiplicación y división como aprendizaje clave.
En el caso de Citlalli, indican las deudas a su cuenta bancaria, en el caso de Carlos la desaceleración y en el caso de los porcentajes, el descuento que se realiza a los productos. Los signos positivos pueden indicar ganancias, pago de deudas e incremento de los precios de los productos, entre otras cosas.
El reto de hoy:
Reflexiona y responde lo siguiente:
¿Qué indican los signos negativos y positivos en una operación matemática con números decimales?
Busca en tu libro de Matemáticas de segundo grado, actividades, problemas y ejercicios para aplicar las reglas de los signos para la multiplicación y división de números decimales positivos y negativos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion