Ángulos y polígonos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: examinar las medidas de los ángulos y las relaciones entre ellos en polígonos regulares.
¿Qué vamos a aprender?
Continuarás con el estudio de un tema muy importante que abordaste anteriormente. En esta sesión, examinarás y determinarás los ángulos interiores, exteriores y centrales de polígonos regulares y la relación que existe entre ellos.
¿Qué hacemos?
Comienza recuperando algunos conceptos y fórmulas para determinar a los ángulos que se forman en los polígonos regulares.
Responde la siguiente pregunta:
¿Qué es un polígono regular?
Un polígono regular es aquél que tiene todos sus ángulos interiores y sus lados iguales.
Ejemplos de polígonos regulares:
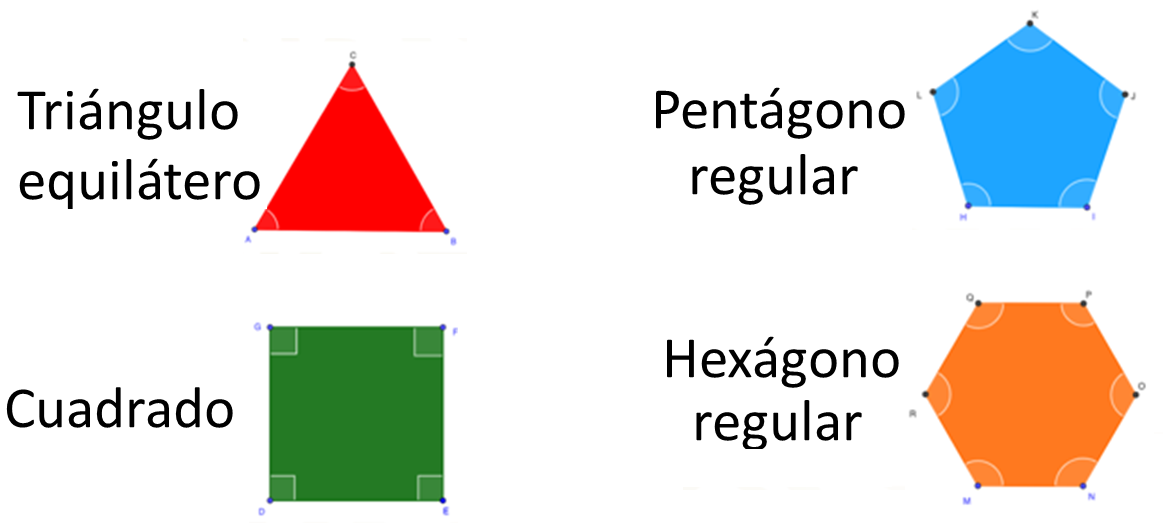
Los ángulos que se presentan en los polígonos regulares son:
- El ángulo interior.
- El ángulo exterior.
- Y el ángulo central.
El ángulo interior de un polígono regular es el que está formado por dos lados consecutivos, coinciden en un vértice y se encuentran en el interior del polígono.
A continuación, observa los ángulos interiores en los polígonos regulares.
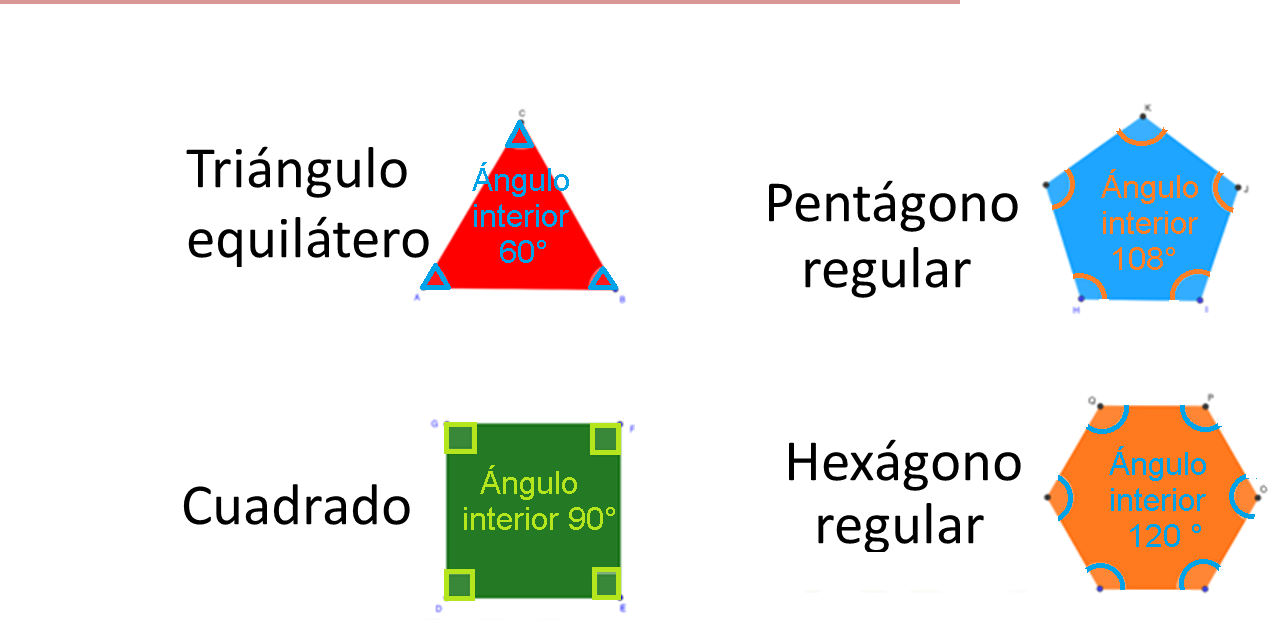
- En el triángulo equilátero, se encuentran 3 ángulos interiores iguales de 60 grados.
- En el cuadrado, 4 ángulos interiores iguales de 90 grados.
- En el pentágono regular, 5 ángulos interiores iguales de 108 grados.
- Y en el hexágono regular, hay 6 ángulos interiores iguales de 120 grados.
La fórmula para calcular el ángulo interior de cualquier polígono regular es:
 .
.
Esta fórmula permite calcular el ángulo interior de cualquier polígono regular. Para ello, basta con sustituir en la fórmula a “n”, que es el número de lados del polígono regular, restarle dos, multiplicar la diferencia por 180 grados y dividir entre “n”.
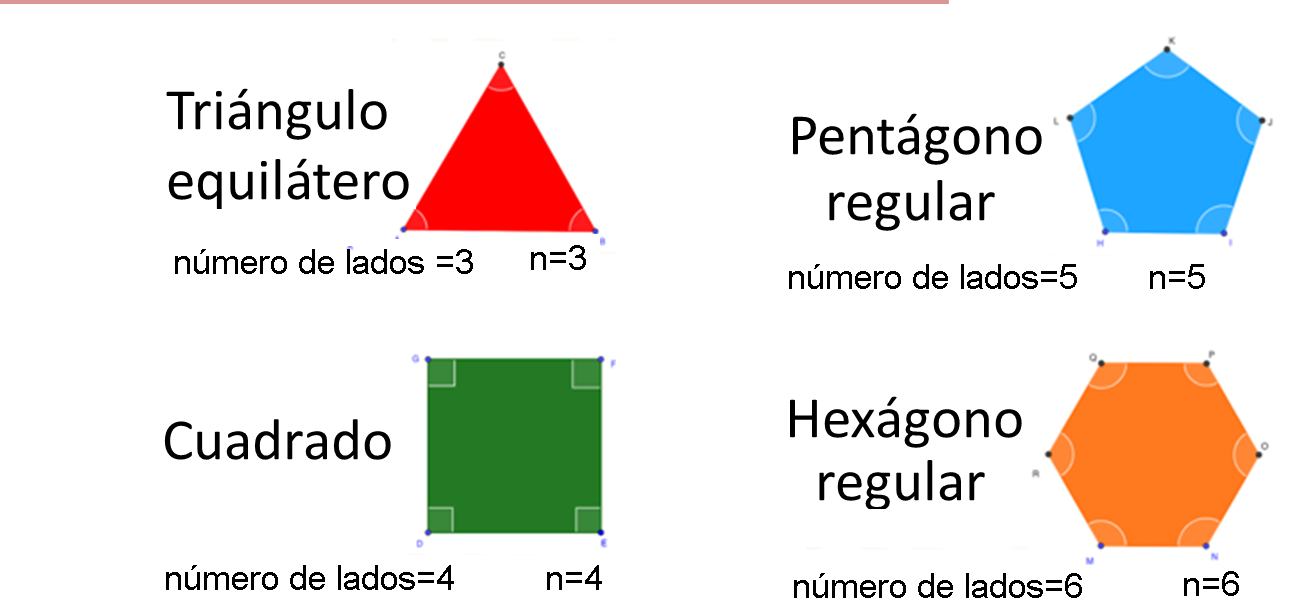
A continuación, observa cómo se obtiene el ángulo interior de las siguientes figuras.
Ángulo interior en el triángulo equilátero:

Este es el valor que se había identificado anteriormente en el triángulo equilátero.
Continúa con las siguientes figuras.
Para obtener el ángulo interior del cuadrado:
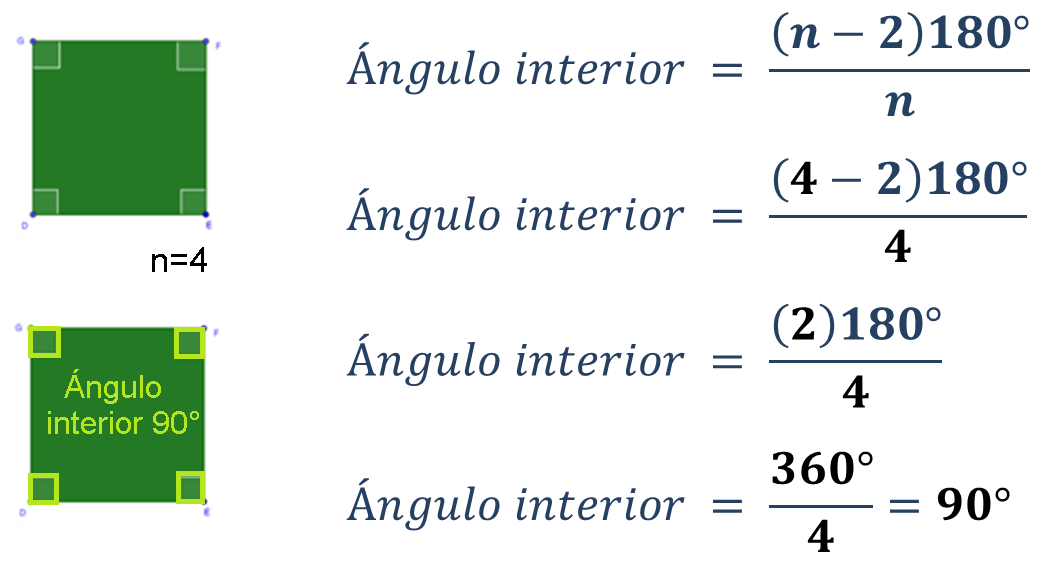
Por lo tanto, 90 grados es el valor en el cuadrado.
Para el pentágono regular:

El valor del ángulo interior en el pentágono regular es de 108°.
Para calcular el ángulo interior del hexágono regular:

102° es el valor del ángulo interior en el hexágono regular.
Ahora, analizarás cómo se calculan los ángulos exteriores de los polígonos regulares. Pero antes, recuerda lo que es un ángulo exterior.
El ángulo exterior de un polígono regular es el que está formado por un lado del polígono y la continuación de su lado adyacente, el cual se encuentra en el exterior del polígono.
Observa los siguientes ángulos exteriores.
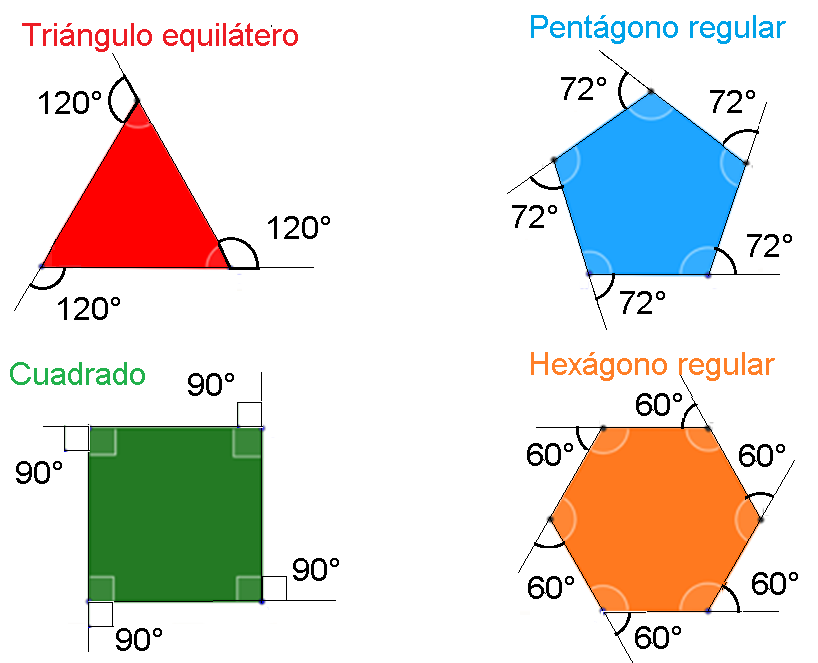
- El triángulo equilátero tiene 3 ángulos exteriores iguales de 120 grados.
- El cuadrado tiene 4 ángulos exteriores iguales de 90 grados.
- El pentágono regular tiene 5 ángulos exteriores iguales de 72 grados.
- Y el hexágono regular tiene 6 ángulos exteriores iguales de 60 grados.
En un polígono regular basta con referirse a un sólo ángulo porque los demás son iguales. Entonces se dice que en un triángulo equilátero el ángulo exterior es de 120 grados, en un cuadrado el ángulo exterior es de 90 grados, en un pentágono regular el ángulo exterior es de 72 grados y en un hexágono regular el ángulo exterior es de 60 grados.
¿Cómo se determinan los ángulos exteriores en los polígonos regulares?
La fórmula para encontrar el ángulo exterior en un polígono regular es:

Porque el ángulo interior y el exterior suman 180 grados, es decir, son suplementarios.
A continuación, observa cómo se obtiene el ángulo exterior de los siguientes cuatro polígonos regulares.
Para el triángulo equilátero se tiene la fórmula:
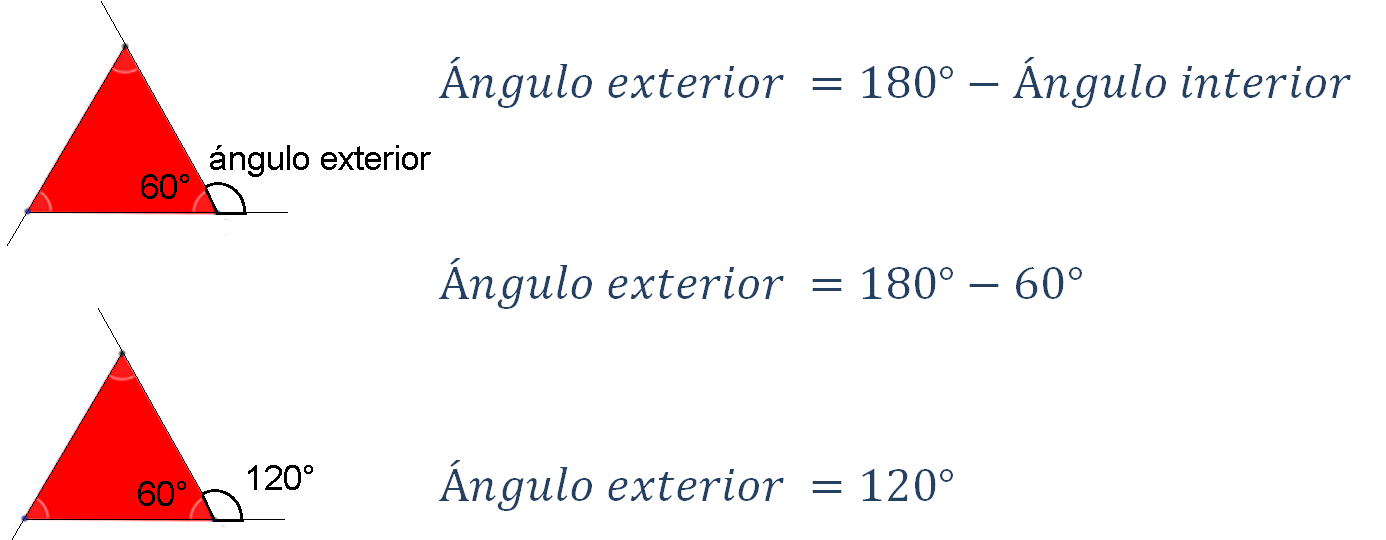
120° es el valor en el triángulo equilátero.
Para el cuadrado se tiene la fórmula:

90° es el valor en el cuadrado.
Para el pentágono regula se tiene la fórmula:

72° es el valor en el pentágono regular.
Y para el hexágono se tiene la fórmula:
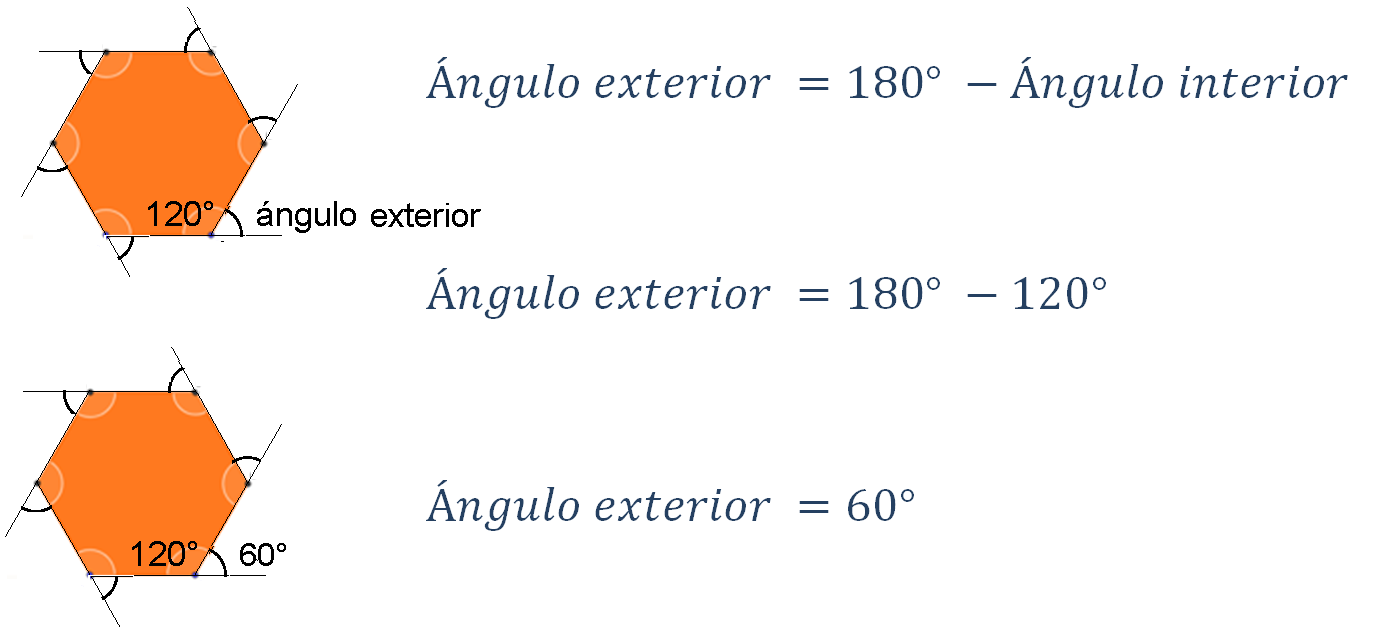
60° es el valor en el hexágono regular.
Antes de revisar cómo se calculan los ángulos centrales de los polígonos regulares, recuerda lo que es un ángulo central.
El ángulo central en un polígono regular es aquel que se forma entre dos segmentos de recta cuyo vértice es el centro del polígono. Estos segmentos van del centro hacia dos vértices consecutivos del polígono.
Observen los siguientes ángulos centrales.
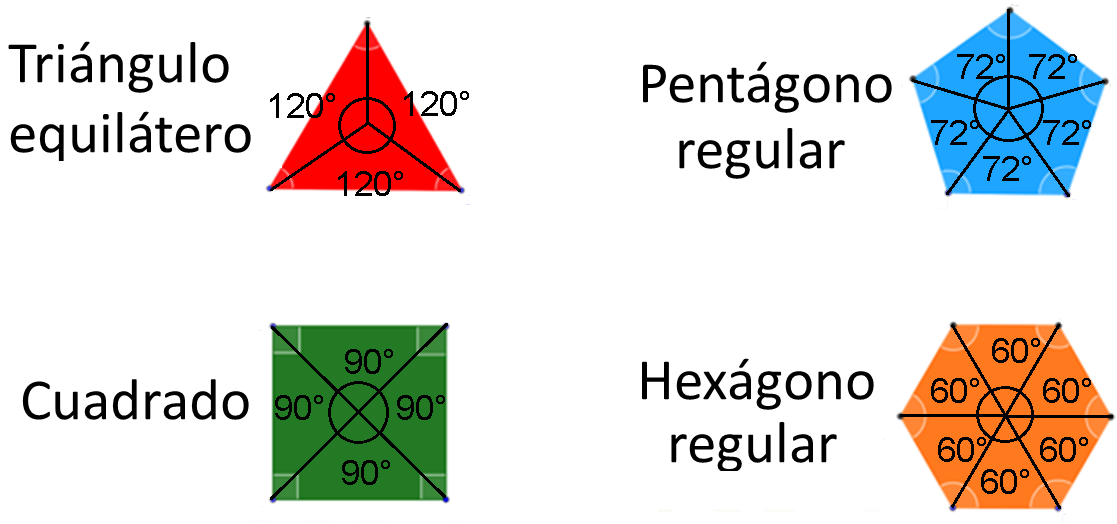
- En el triángulo equilátero se pueden identificar 3 ángulos centrales iguales de 60 grados.
- En el cuadrado, son 4 de 90 grados.
- En el pentágono regular, son 5 de 72 grados.
- Y en el hexágono regular, son 6 de 60 grados.
En un polígono regular basta con referirse a un ángulo para que quede caracterizado. Entonces se dice que, un triángulo equilátero tiene un ángulo central de 120 grados, un cuadrado tiene un ángulo central de 90 grados, un pentágono regular tiene su ángulo central de 72 grados y un hexágono regular tiene su ángulo central de 60 grados.
Una vez identificados los ángulos centrales de los primeros cuatro polígonos regulares, observa cómo se determinan.
La fórmula para calcular el ángulo central de cualquier polígono regular es:

Para calcular el ángulo central de cualquier polígono, sólo tienes que dividir 360 grados entre el número de lados del polígono.
A continuación, observa cómo se obtiene el ángulo central de los siguientes cuatro polígonos regulares.
Para el triángulo equilátero, “n” es igual a 3, entonces:

Por lo tanto, 120° es el valor del triángulo equilátero.
Para el cuadrado, “n” es igual a 4, entonces:

Por lo tanto, 90° es el valor del cuadrado.
Para el pentágono regular, “n” es igual a 5, entonces:

Por lo tanto, 72° es el valor del pentágono regular.
Para el hexágono regular, n es igual a 6, entonces:

Por lo tanto, 60° es el valor del hexágono regular.
Ahora ya sabes qué son y cómo se determina el ángulo interior, exterior y central.
Continúa con la relación que existe entre ellos.
Para conocer la relación que existe entre estos tres ángulos, analiza un octágono regular. Determina e identifica sus ángulos interiores, exteriores y centrales.
Observa el siguiente octágono regular.
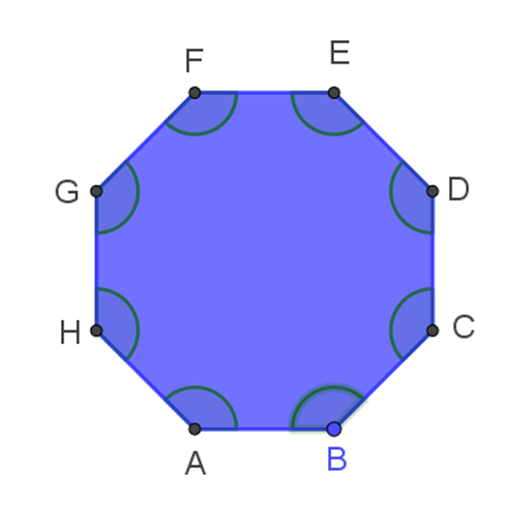
¿Qué características tiene?
Ocho lados iguales y ocho ángulos interiores iguales.
¿Cuál es el valor de su ángulo interior?
El ángulo interior es igual a:
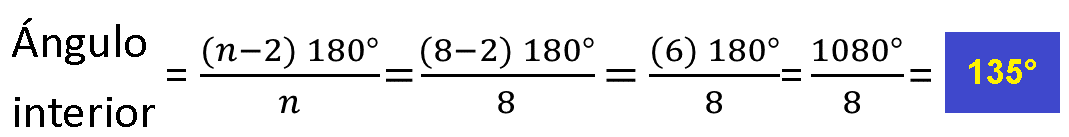
Ahora calcula el ángulo exterior, que es igual a:

Continúa con el cálculo del ángulo central:
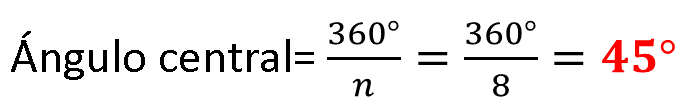
Ahora, ya tienes determinados e identificados los ángulos en un octágono regular:
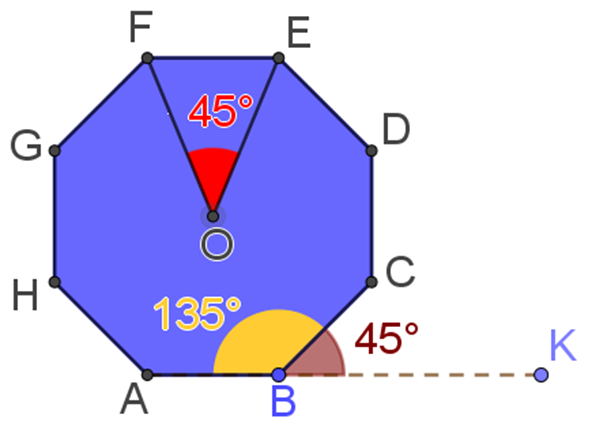
- El ángulo interior de 135 grados.
- El ángulo exterior de 45 grados.
- Y el ángulo central de 45 grados.
Ahora analiza la relación que existe entre estos ángulos.
¿Cuáles son iguales?
Los ángulos exterior y central tienen la misma medida, ambos son de 45 grados.
¿Cuáles son suplementarios?
El ángulo interior y el exterior, porque suman 180 grados; es decir, el interior de 135 grados más el exterior de 45 grados suman 180 grados.
Entonces las relaciones entre los ángulos interior, exterior y central son:
- Los ángulos interior y exterior son congruentes.
- Los ángulos interior y exterior son suplementarios, es decir, suman 180 grados.
¿Por qué es importante conocer estas relaciones?
Porque conociendo alguno de los ángulos se pueden determinar los otros dos. En el caso del octágono, se comenzó con el cálculo del ángulo interior, después del ángulo exterior y después del central.
Reflexiona:
Con el dato del ángulo central del octágono, ¿cómo obtendrías los otros dos ángulos?
Encuentra los ángulos interior y exterior del octágono, si sólo hubieran dado como dato al ángulo central.
Se tiene el dato del ángulo central de 45 grados. Como el ángulo exterior y el central son iguales, entonces el ángulo exterior, es también de 45 grados. Y como los ángulos interior y exterior son suplementarios, entonces el ángulo interior es igual a:
180 - 45 = 135 grados
Has encontrado rápidamente los tres ángulos, ya que conocías la relación entre los tres.
Ahora ya conoces cómo obtener los ángulos interior, exterior y central de los polígonos regulares, y comprendiste las relaciones entre estos ángulos, con las que se pueden determinar dos de ellos a partir del otro.
Pon en práctica estos conocimientos y realiza la siguiente actividad.
Ejercicio, decágono regular
Encuentra el ángulo interior y el central, a partir del dato del ángulo exterior de un decágono regular.
Un decágono, es el polígono regular que tiene 10 lados iguales y 10 ángulos interiores iguales.
El dato con el que cuentas es el valor del ángulo exterior que es de: 36 grados.
Recurre a las relaciones entre los ángulos y realiza el ejercicio.
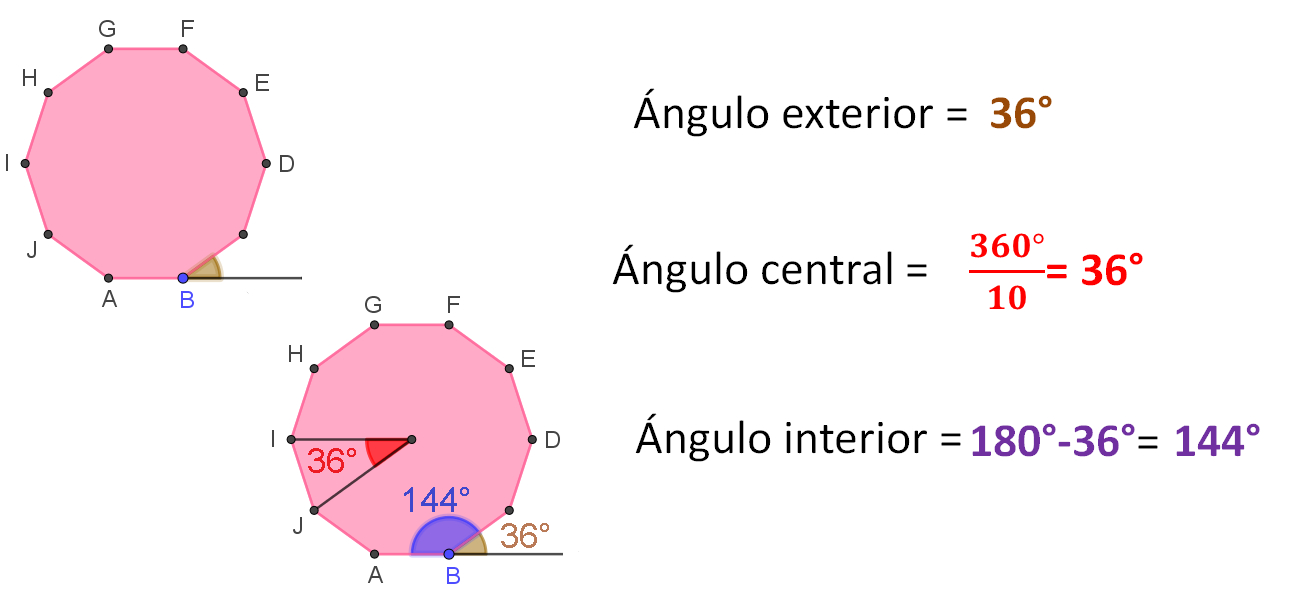
Se sabe que el ángulo exterior es igual al ángulo central, por lo tanto, el ángulo central es igual a 36 grados.
Para calcular el ángulo interior, simplemente realiza la resta:
180 grados - 36 grados = 144 grados
Ahora, calcula los ángulos central e interior a partir del ángulo exterior en el decágono.
Utilizando la relación entre los ángulos interior, exterior y central, puedes obtener el ángulo exterior si conoces el ángulo central. Pero no cuentas con el dato del ángulo central.
Sin embargo, puedes calcularlo de manera rápida porque simplemente se divide 360 entre 10, que son el número de lados del decágono. Y se determina que el ángulo central es igual a 36 grados.
El resultado es igual al ángulo exterior. Y como los ángulos, exterior e interior son suplementarios entonces, se encuentra que 180 grados menos 36 grados es igual a 144 grados, que corresponde al ángulo interior.
Otra estrategia para obtener el resultado es determinar el ángulo interior, pero se necesita el valor del ángulo exterior, entonces se determina con la fórmula, ya que sólo se necesita saber el número de lados que tiene el decágono, los cuales son 10 para sustituirlo en la fórmula.
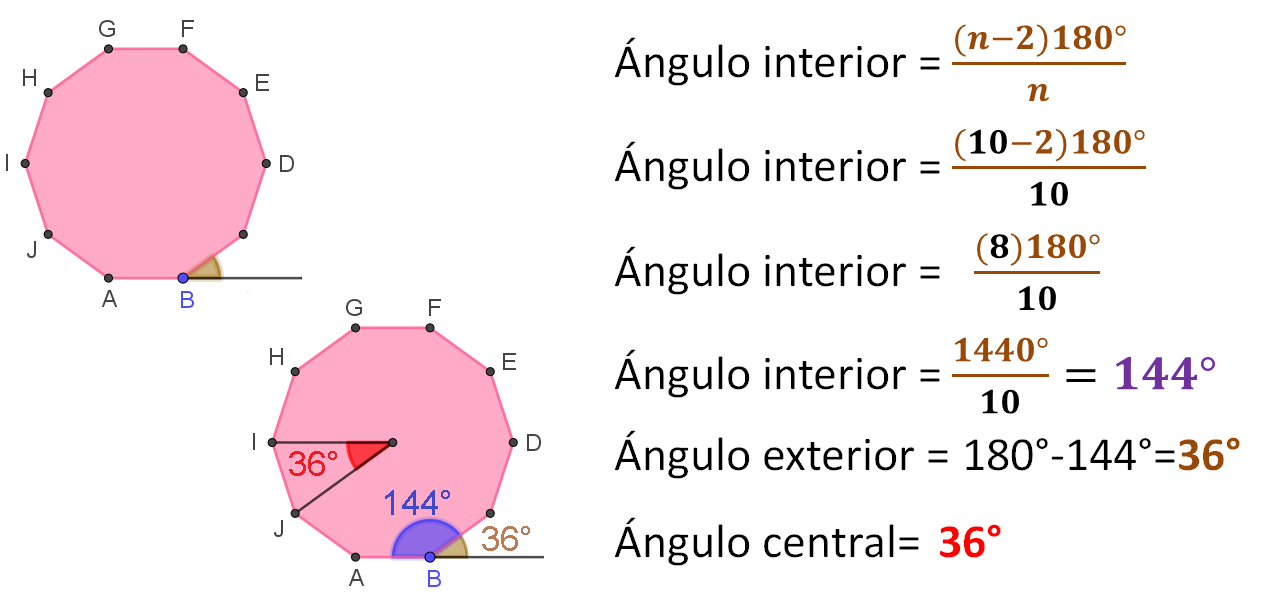
Esta es otra manera de resolver el ejercicio.
Observa que dependiendo de los datos del problema será la estrategia a utilizar. Ya que muchas veces, hay más de una forma de resolver un ejercicio, problema o situación.
La primera estrategia consistió en utilizar la relación entre los ángulos interior, exterior y central, y en la segunda se recurrió a la ayuda de la fórmula que se había utilizado anteriormente para calcular el ángulo interior y posteriormente se regresó al concepto de las relaciones entre los tres ángulos para encontrar los ángulos central y exterior.
En esta ocasión recordaste qué son los ángulos interior, exterior y central de un polígono regular, también aprendiste a determinarlos o calcularlos, ya sea mediante las fórmulas o por medio de las relaciones entre éstos.
Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendiste aquí.
El reto de hoy:
Realiza lo siguiente:
Determina los ángulos exterior y central en un dodecágono regular, a partir de su ángulo interior, dibuja el polígono indicando sus ángulos y márcalos con diferentes colores.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:





Login to join the discussion