La cooperativa de manteles
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:08
La cooperativa de manteles
Aprendizaje esperado: construye configuraciones utilizando figuras geométricas.
Énfasis: discrimina información geométrica para realizar una configuración.
¿Qué vamos a aprender?
Aprenderás a construir configuraciones utilizando figuras geométricas.
¿Qué hacemos?
Vas a necesitar el siguiente material.

https://libros.conaliteg.gob.mx/20/P1MAA.htm
2 hojas blancas de tamaño carta, colores, hojas recicladas de cualquier color, pegamento, tijeras y tu libro de texto.
Es muy importante tener tu material listo, sino lo tienes, ve por él.
También es importante que tu espacio de trabajo esté despejado y limpio para que puedas trabajar cómodamente. Recuerda que no debe de haber comida o líquidos porque si algo se cae, podría ensuciar tu trabajo.
¿Tú sabes qué es una cooperativa?
En tu escuela le llamas cooperativa a la tiendita en donde vendían la comida que comprabas a la hora del recreo.
¿Y por qué se llama cooperativa y no simplemente tiendita?
La cooperativa es una sociedad que se forma entre productores, vendedores y consumidores para el beneficio común de los socios.
Las cooperativas de la escuela tienen como función promover la solidaridad, el ahorro, la iniciativa, la ayuda mutua, la responsabilidad, la convivencia, entre otros valores. Parte de los ingresos de la cooperativa escolar se destinan para apoyar necesidades de la escuela, otra para mantener activa la cooperativa y otra parte, se reparte entre los socios, en este caso los socios son todas y todos los que estudian y trabajan en esa escuela.
Por eso es que te dan al final del año una parte de la ganancia. ¿Y cómo relacionas la cooperativa con la sesión de matemáticas?
Pues que para esta sesión harás una cooperativa en la que vendas manteles. ¿Recuerdas los tapetes que hacían los artistas de Teotitlán del Valle? Pues también diseñaras con figuras geométricas, pero manteles.
Abre tu libro en la página 188
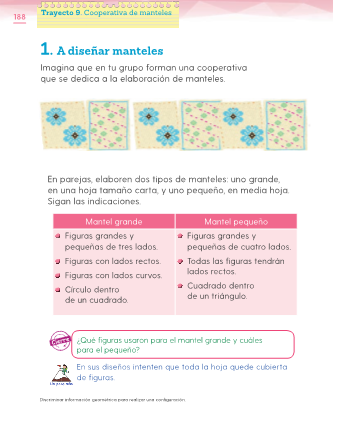
La actividad que te proponen consiste en producir para tu cooperativa dos tipos de manteles, uno pequeño y otro grande. Aquí en la tabla vienen las características de cada mantel.

El libro te pide que dibujes los manteles, pero se agregan recortes de figuras geométricas, para hacerlo aún más divertido.
Haz la actividad, empieza haciendo el mantel grande.
El mantel grande se hace en una hoja blanca tamaño carta. La primera instrucción dice que debe tener figuras grandes y pequeñas de tres lados.
¿Qué figura conocen que tiene 3 lados? Triángulo.
Recorta triángulos de colores.
También puedes dibujarlos. Recuerda hacer triángulos grandes y pequeños, si los recortas debes pegarlos sobre la hoja blanca. Mientras las pegas vas a leer la siguiente característica, dice “Figuras con lados rectos”.
Los triángulos son figuras de lados rectos.
Pero, ¿Qué otras figuras puedes agregar? Cuadrado.
También puedes incluir cuadrados. Vas a recortar un cuadrado grande y otro pequeño.
La tercera instrucción dice que dibujes figuras con lados curvos. ¿Qué figura podrías dibujar? Círculo.
El círculo es una figura con un lado curvo. ¿Un medio círculo es una figura con un lado curvo?
Un medio círculo es como si doblaras el círculo a la mitad o si lo cortaras con las tijeras. Un medio círculo tiene un lado recto y otro curvo.
Entonces te propongo que agregues a tu diseño círculos y medios círculos.
Puedes elegir las figuras que más te gusten, no necesariamente debes de elegir las mismas figuras que se están comentando. La única condición es que cumpla con las características que te dice el libro.
Ya tienes tu diseño de mantel grande: triángulos, cuadrados, círculos y medios círculos. ¿Qué otra característica te pide?
La cuarta característica del mantel grande es que tenga un círculo dentro de un cuadrado.
Te propongo que el cuadrado sea hecho con un recorte y que le dibujes un círculo encima.
En cuanto ya vayas terminando tus manteles, compártelo con la persona que te acompañe, diles qué figuras geométricas escogiste para tus diseños.

¡Qué bonito diseño! Hay triángulos, cuadrados, círculos y medios círculos.
Te comparto los diseños de compañeros de primer grado son de Raquel y Tomás.


Vas a observar si los diseños cumplen con las características que pide el libro. El de Raquel tiene triángulos que dibujó y recortó, es decir, que sí tiene figuras de 3 lados.
Las figuras de 3 lados siempre se van a llamar triángulos, aunque sus lados pueden ser de distinto tamaño.
El mantel de Tomás también tiene triángulos pequeños y rojos. La siguiente característica pide el libro es figuras con lados rectos, además del triángulo, Raquel dibujó rombos y Tomás recortó trapecios.
¿Pero qué otra figura de lados rectos encuentras en el diseño de Tomás?
También tiene la figura que parece una casita.
Esa figura se llama pentágono y tiene 5 lados rectos. ¿Y esa figura que parece una celda de panal de abejas?
Esa se llama hexágono.
Ahora dime, ¿Qué tienen en común un cuadrado, un rombo y un trapecio?
El cuadrado, el rombo y el trapecio son figuras con 4 lados rectos. Y aunque los trapecios del diseño de Tomás están colocados sobre distintos lados, siguen siendo trapecios.
¿Recuerdas alguna otra figura de 4 lados rectos que has conocido aquí en la sesión?
El rectángulo y el romboide; el romboide es como un rectángulo, pero con dos de sus lados inclinados.
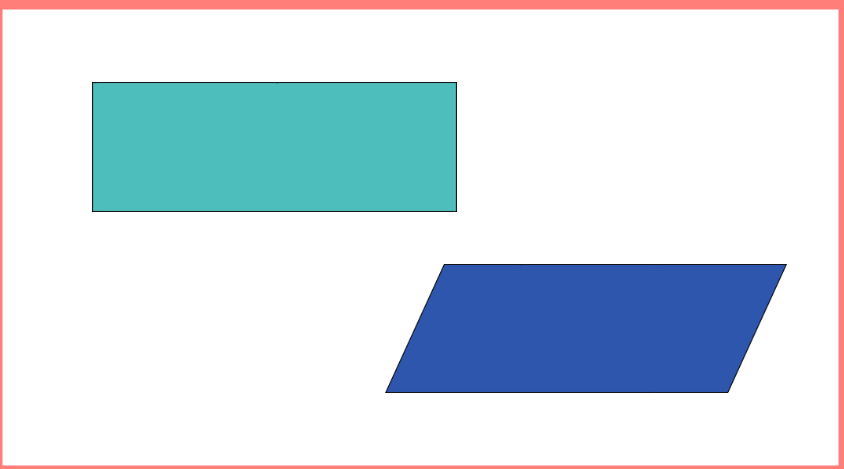
La siguiente instrucción te pide figuras con lados curvos. ¿Qué hizo Raquel?
Raquel dibujó un círculo, pero como aplastadito.
Recuerda que ese círculo aplastadito se llama óvalo.
Tomás también recortó círculos. La última característica que debía tener el mantel era tener un círculo dentro de un cuadrado. Lo que se hizo en la primera imagen fue recortar un cuadrado y después dibujarle un círculo adentro.
Raquel hizo al revés; dibujó un cuadrado y adentro le pegó un círculo. Raquel y la primera imagen cumplen con la instrucción solicitada, pero se usaron distintos materiales y por eso su diseño es único.
Tomás también cumplió con la instrucción, pero su diseño de mantel está hecho solamente a base de recortes de hojas de colores.
Ahora te corresponde hacer el mantel pequeño. Lo primero que tienes que hacer es recortar la hoja blanca a la mitad. ¿Cómo le haces para calcular dónde es la mitad de la hoja?
Doblas la hoja a la mitad y después recortas sobre la línea que dejó el doblez.
Lee la primera característica que te pide el libro para el mantel pequeño. Dice: figuras grandes y pequeñas de 4 lados. Acabas de repasar algunas figuras de 4 lados; te propongo que las uses todas. Puedes dibujarlas o recortarlas y pegarlas.
Repasa en voz alta, los nombres de algunas figuras geométricas de 4 lados.
Cuadrado, rectángulo, rombo, trapecio y romboide.
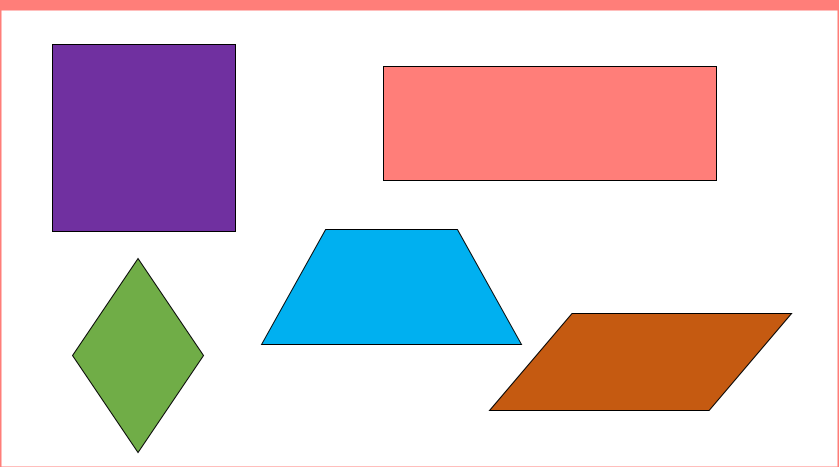
Ahora la de las figuras con un solo lado recto: círculo y óvalo.

Las figuras de 5 lados son pentágonas.
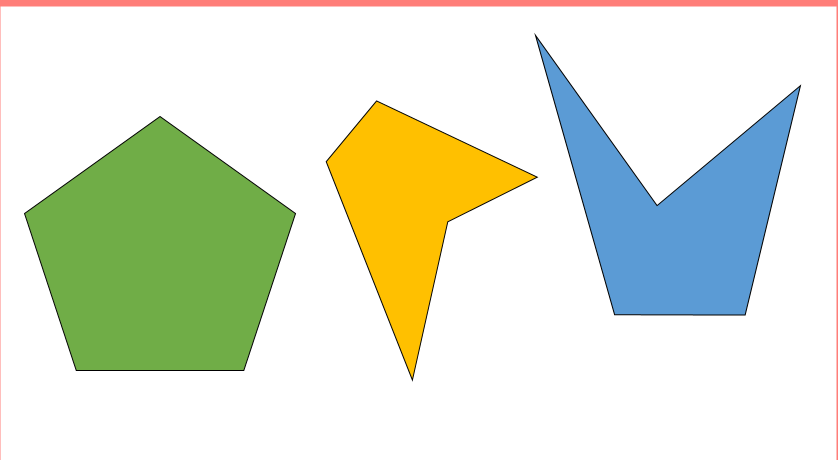
Y las figuras de 6 lados se llaman hexágonos.
¿Ya terminaste?
Te muestro otro ejemplo.

También te comparto los dibujos de Andrea y Benito de primer grado.


Los tres manteles tienen figuras grandes y pequeñas de 4 lados, todas las figuras que dibujaron tienen lados rectos y en los tres manteles hay un triángulo dentro de un cuadrado. Muy bien, hicieron un gran trabajo. Quiero que analices a detalle los diseños de cada quien. En el primer diseño, ¿cómo se llama la figura amarilla?
La figura amarilla es, al igual que la morada, un cuadrado, la única diferencia es que la figura amarilla está posicionada sobre uno de sus vértices. Si te das cuenta el rombo es más alargadito. Otra cosa que quiero que observes del dibujo es la composición del cuadrado con un triángulo adentro, si juntaras estas dos composiciones moradas qué figura te daría.
Si las juntaras sería un rombo dentro de un rectángulo.
Andrea no sólo dibujó el triángulo dentro del cuadrado, sino que también dibujó rombos pequeños dentro de rombos grandes. ¡Qué gran idea! Se ve muy bonito.
Lo que llama mucho la atención del diseño de Benito fue que utilizó otra herramienta que has aprendido en las sesiones: los patrones. En la línea de figuras que recortó el patrón es un cuadrado vino, uno amarillo, uno rojo y un rombo verde, y luego se repite el patrón.
Otro aspecto interesante en el mantel de Benito, es que jugó con los tamaños de las figuras. Hizo un gran rectángulo azul que enmarcó todas las demás figuras pequeñas.
Las posibilidades son tantas como las que te puedas imaginar.
Se ha terminado esta sesión, pero continúa haciendo los manteles. Has diseños distintos, puedes agregar otros materiales y texturas, siempre y cuando formes figuras geométricas.
El reto de hoy:
Invita a las personas que viven contigo a diseñar manteles para la cooperativa.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas






Login to join the discussion