De viaje hasta Alaska
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57
De viaje hasta Alaska
Aprendizaje esperado: relaciona unidades del Sistema Internacional de Medidas con las unidades más comunes del Sistema Inglés.
Énfasis: elige las operaciones que permiten resolver problemas donde es necesario comparar unidades de peso y capacidad de los sistemas inglés (libra, onza y galón) e Internacional.
¿Qué vamos a aprender?
Aprenderás a relacionar las unidades el Sistema Internacional de Medidas con las unidades más comunes del Sistema Inglés, para ello elegirás las operaciones que te permitan resolver los problemas que requieren comparar unidades de peso y capacidad de los sistemas Inglés (libra, onza y galón) e Internacional.
¿Qué hacemos?
Continuarás realizando exploraciones, retos y recorridos muy interesantes, así que prepárate para esta experiencia, hoy viajarás hasta Alaska donde vive Moaed, que es la hija del tío Ángel, quien visitaste la sesión pasada. Así que prepara tus maletas de conocimientos, mucha ropa de invierno y ¡Vámonos de viaje hasta allá!
Los materiales que requieres tener a la mano son: mucha disposición, tu libro de texto de Desafíos Matemáticos de sexto grado, lápiz, goma y sacapuntas.
Alaska es uno de los cincuenta estados que forman Estados Unidos de América. Su capital es Juneau, ¡es un lugar donde hace mucho frío! Su ciudad más poblada es Anchorage.

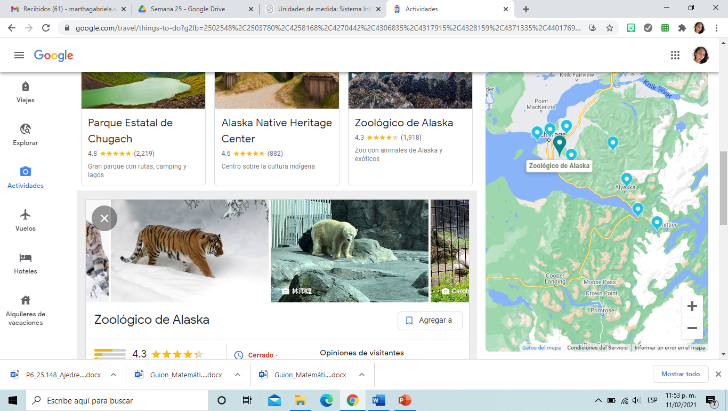
En Alaska hay muchos sitios turísticos: el museo de Anchorage, el zoológico de Alaska, glaciares, su parque nacional, en fin, todo siempre cubierto de nieve.
En esta ocasión María te comparte la experiencia que vivió con su prima, la hija del tío Ángel, Moaed, quien cuando llegó a su casa de visita en Alaska, le había dejado una nota donde decía que tardaría en llegar, pero que se acomodara y que pusiera sus maletas en el mueble de la recámara, siempre y cuando no pesaran más de 50 libras.
María sabía que sus dos maletas tenían un peso, la primera de 20 kg y la segunda de 25 kg.
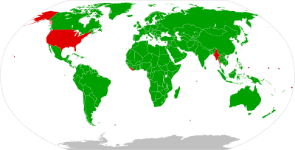
Ayer observaste en un planisferio los países que utilizan el Sistema Internacional de Medidas y los que no lo usan. Ahora puedes observar este planisferio que muestra que Alaska, Estados Unidos de América y Myanmar están en rojo, donde es oficial la libra y no ha sido sustituida por el kilogramo.
La libra es una unidad de peso del sistema inglés, equivale a 0.454 kilogramos.
Esas unidades para medir el peso, son diferentes a las que se utilizan en México. ¿Qué tuvo que hacer María para saber que el peso de sus maletas no vencía el mueble?
Como la libra equivale a 0.454 kg. para conocer el peso que aguanta el mueble, sólo multiplicó 50 por 0.454 porque el mueble soporta sólo 50 libras.
Observa la operación:
0.454 x 50 = 22.700
Entonces, como puedes observar, María solo pudo guardar una maleta en ese mueble.
María comenta que cuando fue a la cocina, su prima le hizo un encargo, que consistió en lo siguiente:
Pidió 3 onzas de aceite de aguacate.
¿Onzas? ¿A qué se refiere con eso?
La libra es la unidad que usan para el peso, pero para medir los líquidos utilizan también otras unidades de medida diferentes del litro; una de ellas es la onza líquida y se abrevia oz.
Por ejemplo, los biberones tienen las letras oz.

La onza se utiliza tanto como medida de peso como de capacidad, la de capacidad se llama onza líquida, su uso es muy común en los países anglosajones. Como norma general, una onza equivale a 0.283 kilogramos, cuando se trata de la onza para saber pesos; y la onza líquida que equivale a 29.57 mililitros.
Para cumplir con el encargo que le hizo su prima a María, llevó botellas de 50 ml.
¿Cuántas de esas botellas equivalen a 5 onzas?
Para saberlo, hay varios caminos que se pueden seguir, por ejemplo, ya sabes que la onza líquida equivale a 29.57 ml. Entonces para calcular el equivalente en mililitros de cinco onzas líquidas debes multiplicar.
29.57 x 5 = 147.85 ml.
Y para saber a cuánto equivalen las 5 botellas, multiplica:
50 x 5 = 250 ml.
Que equivale a 0.250 litros, o sea una cuarta parte del litro.
Así que María encontró que requería usar tres frascos.
50 x 3 = 150 ml.
Entre los tres tienen una capacidad de 150 ml, por lo tanto, cabrán bien 147.85 mililitros.
Es claro que tres botellas de 50 ml son suficientes para llenar un recipiente de 5 onzas.
¿Sabes o recuerdas alguna otra unidad de medida con la que se midan los líquidos?
Seguramente has escuchado de otra medida nombrada como “galón”
Un galón es el equivalente a 3 litros con 785 mililitros.
Como puedes observar en la siguiente imagen hay envases de diversos tamaños, a unos les cabe un galón y otros tienen la medida tanto en onzas como en mililitros.


Es momento de comprobar algunas equivalencias.
Se tiene una botella de medio galón, entonces ¿cómo puedes saber su equivalencia en litros?
Debes recordar primero que la equivalencia del galón es de 3.785 litros.
Y para saber cuánto es medio galón, se divide entre dos.
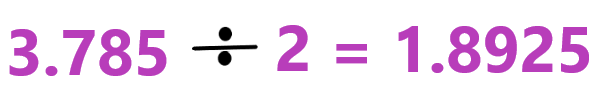
Es un poco menos de dos litros, si sólo hubiera envases de un litro, entonces medio galón alcanzaría para llenar el de un litro y el segundo envase quedaría un poco menos lleno, pues medio galón no llega a 2 litros.
Ahora, en un biberón es más fácil apreciar la equivalencia ya que están al lado ambas graduaciones, tanto en onzas como en mililitros.
En un biberón puedes observar que 5 onzas casi son 150 mililitros, realiza las operaciones para comprobarlo, piensa en casa qué tendrías que hacer.

Primero debes recordar que una onza líquida equivale a 29.57 mililitros y puedes multiplicar esta cantidad por 5.
29.57 ml x 5 oz =
Como una onza es 29.57 basta con multiplicar 5 por 29.57 para obtener el resultado.
1 oz = 29.57
5 x 29.57 = 147.85
Por eso puedes observar en el biberón, que está ligeramente abajo la raya de las 5 onzas, con respecto a los 150 mililitros.
Es momento de que vayas al Desafío 45, que está en la página 96 de tu libro de texto, Desafíos Matemáticos, donde también te preguntan sobre equivalencias del sistema inglés y el sistema internacional, precisamente se llama Libra, onza y galón.
La consigna dice:
En parejas resuelvan el siguiente problema: los padres de Luis le están organizando una fiesta de cumpleaños. Ayúdenles a seleccionar la presentación de galletas y de jugos que más convenga, considerando su precio y contenido, pueden consultar las equivalencias en los recuadros y utilizar su calculadora.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/96

Observa la información que te dan de las galletas para comparar los precios de las diferentes presentaciones.
Si te fijas bien, sólo que el peso de las galletas está dado en diferentes unidades.
Es importante que primero transformes todos los contenidos a la misma unidad de medida. Una de las medidas está dada en onzas, como se dijo anteriormente, las onzas no se utilizan para medir líquidos. Hay onzas para medir peso y onzas para líquidos.
Para distinguirlas, a una se le llama onza líquida y a la otra simplemente onza, así que en este caso no se está usando la onza líquida.
Primero convierte todo a kilogramos y utiliza las conversiones que están en la página.

La primera presentación es una caja de 44.17 oz Multiplica, si tienes calculadora, también la puedes usar:
44.17 x .0283 = 1.250011
En términos generales se puede decir que es 1 kilogramo con 250 gramos y su costo es de $62.90
Para saber el precio del kilogramo puedes dividir el precio total entre 1.250 y obtendrás el precio por kilogramo.
1.250 kg ------ $62.90
1 kg ------ x

Por lo tanto, el kilogramo en esta presentación cuesta $50.32
Ahora la segunda presentación ya está en kilogramos:
1 kg = $48.00
Sólo queda transformar la última presentación de galletas que cuesta $37.50 pero su peso está dado en libras y onzas, puedes reconocer que una libra es menos de medio kilogramos, y, de acuerdo con la tabla de equivalencias, se puede decir que una onza es igual a un poco más de 28 gramos.
Para cuestiones prácticas la equivalencia de la onza sea sólo de 28 gramos y observa entonces cuál es el peso total de la tercera caja. Dos libras equivalen a 908 gramos, pero ¿A cuánto equivalen las 10.46 onzas?
Analiza el desafío, si una onza equivale a 0.0283 kilogramos, eso quiere decir que la onza es 28.3 gramos aproximadamente, porque un kilogramo tiene 1000 gramos.
¿A cuánto equivalen 10 onzas?
Multiplica 28.3 x 10 diez onzas son 283 gramos. ¿A cuánto equivale la parte decimal de las onzas, pues se tiene 10.46 onzas?
Para saber a cuántos gramos equivalen los 46 centésimos de onza, se puede multiplicar 28.3 por 0.46 y así conocerás a cuántos gramos equivale:
1 oz ------ 28.3 gramos
0.46 oz ----- x gramos
28.3 x 0.46 = 13.018
El resultado indica que los 46 centésimos equivalen a casi 13 gramos, así que la caja de galletas de la tercera presentación pesa aproximadamente:
908 + 283 + 13 = 1 204 gramos.
Es decir, 1.204 kilogramos.
La tercera caja pesa un poco más de un kilogramo con doscientos gramos y cuesta $37.50
Y puedes hacer lo mismo que ya hiciste antes para saber cuánto cuesta el kilogramo de estas galletas.
Si divides el precio de la caja de galletas, entre el peso que contiene, puedes obtener el precio de un kilogramo.
1.204 kg ------ $37.50
1 kg ------ x

Así que el kilogramo de la tercera caja cuesta $31.14
Finalmente puedes identificar que esta última caja de galletas es más económica, pues el kilogramo cuesta menos.
Ahora comprueba cuál de las tres presentaciones de jugos te conviene más.
La primera es un paquete que contiene cuatro piezas de 6.76 oz c/u envase y su precio es de $9.40
Primero multiplica 6.76 por 4 para saber la cantidad total del paquete, si tienes calculadora úsala.
6.76 x 4 = 27.04 oz
Una onza líquida equivale a 29.57 mililitros, así que debes multiplicar para saber a cuántos mililitros equivalen 27.04 onzas, si tienes calculadora úsala.
27.04 x 29.57 = 799.5728
Como el resultado está en mililitros, conviértelo a litros recorriendo el punto, pues ya sabes que un litro es igual a 1000 mililitros, entonces divide 9.40 entre 0.799
0.799 litro ------- $9.40
1 litros ------- x
Así que el litro cuesta $11.76
La segunda presentación del jugo señala que el litro cuesta $12, así que está un poquito más caro.
Por último, ya sabes que un galón cuesta $47.10 y además un galón equivale a 3.785 litros.
3.785 -------- $47.10
1 litro --------- x
De lo cual se puede obtener que el litro cuesta $12.44 por lo que conviene comprar la primera presentación.
Como te podrás dar cuenta, es muy interesante conocer todas las equivalencias, porque de esa manera cuando la presentación esté en otra unidad de medida sabrás qué es lo que más te conviene comprar, ahora es muy común encontrar que varios envases traen unidades de medida en el sistema inglés.
En esta sesión conociste nuevas unidades de medida, también supiste que, si llegas a viajar a otros países, podrás hacer conversiones de monedas o de medidas de peso y capacidad con mayor facilidad y eso te servirá en tu día a día.
El reto de hoy:
Comenta con alguien cercano, lo que aprendiste sobre las equivalencias de ambos sistemas de medida y explícale como puedes usarlas y por qué son importantes. Si tienes algunos productos en casa, identifica en que medidas vienen y atrévete a usar las equivalencias para convertirlos a las medidas que se usan en este país.
Si te es posible, consulta otros libros y materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion