Lápices y libretas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: determina divisores o múltiplos comunes a varios números. Identifica, en casos sencillos, el mínimo común múltiplo y el máximo común divisor.
Énfasis: usa las nociones de múltiplo común y divisor común para validar algunas afirmaciones sobre sus regularidades.
¿Qué vamos a aprender?
Determinarás divisores o múltiplos comunes a varios números. Identificarás, en casos sencillos, el mínimo común múltiplo y el máximo común divisor; y usarás las nociones de múltiplo común y divisor común para validar algunas afirmaciones sobre sus regularidades.
¿Qué hacemos?
Trabajarás con el tema de múltiplos y divisores comunes, cada día te es más fácil resolver las situaciones relacionadas con esos temas, también has tenido la oportunidad de conocer e identificar ciertas regularidades que caracterizan a los números que son múltiplos de un número natural y a los números que son divisores de algunos números. Esto te permite conocer mejor, en este caso, a los números naturales.
En la sesión de ayer y en la página 138 de tu libro de desafíos, se te pidió encontrar los divisores comunes de 3, 9 y 12 o de 90 y 70 si ya los encontraste sería conveniente que escribas un contexto o una situación que implique esos valores.
El desafío de hoy tiene que ver con los divisores comunes de dos o más números, conocerás una situación más, donde usarás múltiplos y divisores comunes de dos o más números para resolverla. Ve el desafío número 75 que está en la página 139

La consigna dice lo siguiente:
Resuelve los siguientes problemas.
-
Al hacer paquetes de 6 libretas y paquetes de 6 lápices de colores, los maestros de una escuela se percataron de que había más paquetes de lápices que de libretas, y de que en ambos casos no sobraba nada. Se sabe que la cantidad original de libretas está entre 185 y 190, y la de lápices, entre 220 y 225 ¿Cuál será la cantidad original de libretas y lápices de colores?
Procede a resolver el problema por partes, primero debes encontrar la cantidad de libretas y después la cantidad de lápices, ir por partes te ayuda a no desesperarte y confundirte, piensa en la información que te dan, y en lo que te piden, señalan que en cada paquete de lápices y libretas había 6 así que este número es importante para la solución, también señala que el número de libretas era entre 185 y 190
6 libretas en cada paquete, entre 185 y 190 libretas
Eso significa que los maestros de esa escuela contaban con 185 libretas o, tal vez, 186 o 187 o 188 o 189 o 190 libretas, eso significa, ahora te toca identificar cuál de éstos fue el número exacto de libretas que tenían. ¿Tienes alguna idea de cómo podrías saberlo?
De acuerdo con la información que tienes, los maestros formaron paquetes con seis libretas cada uno, así es, cada paquete está formado por seis libretas, independientemente de la cantidad total exacta de libretas, entonces puedes recurrir a la división, sería dividir cada posible cantidad total de libretas entre seis. ¿Por qué dividir cada cantidad entre seis? Es decir, ¿Por qué crees que la división ayude?
Porque al dividir las posibles cantidades entre el número de libretas puedes ver en cuál división, el residuo es cero, es decir, en cuál división no sobran libretas.
Antes de continuar debes recordar las características que debe tener un número para considerarlo divisor de otro y que al hacer la división, el residuo sea cero.

Una de las principales características es que cuando al hacer la división se obtiene como residuo cero. La otra característica importante es que el cociente debe ser un número natural, no puede ser un número decimal.
Ahora sigue con la propuesta de dividir cada posible cantidad de libretas entre seis que es el número de libretas que forman un paquete.

Identifica cuál de estas divisiones que vas a realizar será la que dé el resultado que estás buscando. La división donde se cumpla que el cociente es un número entero y el divisor es cero, adelante, comienza a dividir.
185 ÷ 6 = 30.8
186 ÷ 6 = 31
187 ÷ 6 = 31.16
188 ÷ 6 = 31.13
189 ÷ 6 = 31.5
190 ÷ 6 = 31.6
Ya apareció la única división con residuo cero es ciento ochenta y seis entre seis, que da treinta y uno, pero ese resultado no corresponde a la cantidad de libretas.

Ese resultado corresponde a la cantidad de paquetes de libretas que se formaron, entonces la respuesta de cuál es la cantidad original de libretas es ciento ochenta y seis.
Ahora pasa a los paquetes de lápices de colores, aquí podrías seguir el mismo procedimiento, pero ahora debes considerar las posibles cantidades de los lápices de colores. ¿Recuerdas cuáles eran? Estaba entre 220 y 225. Realiza un procedimiento semejante al anterior.

En este caso las divisiones a efectuar son:
220 ÷ 6 = 36.6
221 ÷ 6 = 36.83
222 ÷ 6 = 37
223 ÷ 6 = 37.16
224 ÷ 6 = 37.3
225 ÷ 6 = 37.5
Como puedes observar, la solución es el número doscientos veintidós que representa la cantidad original de lápices de colores que los maestros tenían para formar los paquetes, entonces la respuesta al problema planteado en los desafíos es que la cantidad de libretas que había era 186 y la cantidad de lápices de colores era 222 y aunque no lo preguntaron en el problema, otra información que también pudiste encontrar al resolverlo fue que se formaron 31 paquetes de libretas y 37 paquetes de lápices.

Ahora pasa al punto dos del desafío, observa la siguiente tabla.

La consigna dice lo siguiente:
Lean y discutan las siguientes afirmaciones. Concluyan si son verdaderas o falsas y expliquen su decisión.
Elige la que quieras, puede ser la siguiente:
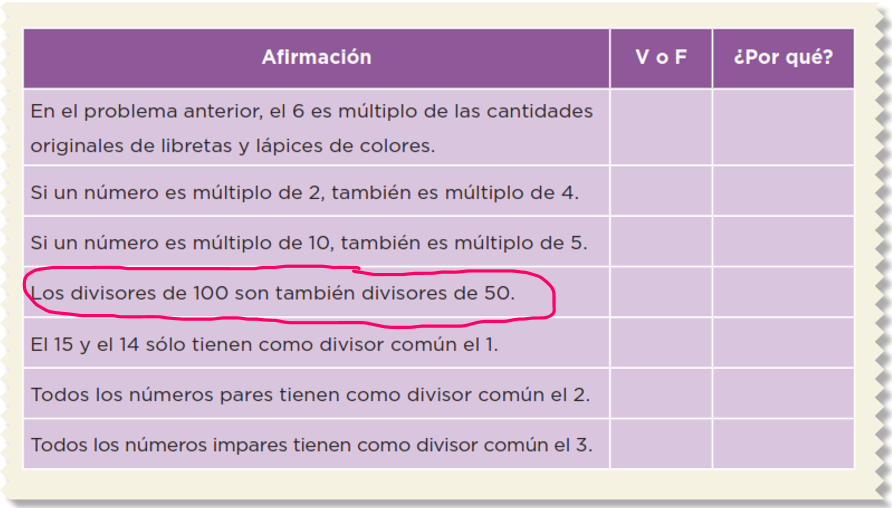
Los divisores de cien son también divisores de cincuenta.
¿Cuál sería tu respuesta? ¿Es verdadero? ¿Por qué consideras que es verdadero? Sencillo, si sabes que cien es múltiplo de cincuenta, por lo tanto, todos los divisores de 50 son divisores de 100. Como ayer con los números con los que jugaste a la subasta, el 30 y el 60 pero, analízalo, ¿Cuáles son los divisores de 50? Son 1, 2, 5, 10, 25 y 50 porque
1 x 50 = 50
2 x 25 = 50
5 x 10 = 50
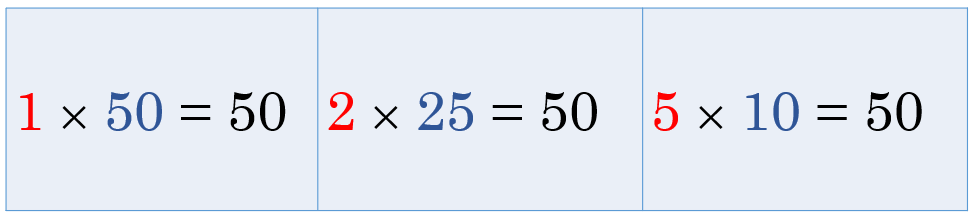
Y ahora, ¿Cuáles son los divisores de 100?

Son 1, 2, 4, 5, 10, 20, 25, 50 y 100 porque:
1 x 100 =100
2 x 50 =100
4 x 25 =100
5 x 20 =100
10 x 10 =100
Es cierto que todos los divisores de 50 son también divisores de 100 pero no se cumple al revés, es decir, no todos los divisores de 100 son divisores de 50 por ejemplo, el 20 es divisor de 100 pero al dividir 50 entre 20 el cociente no es un número natural o entero.
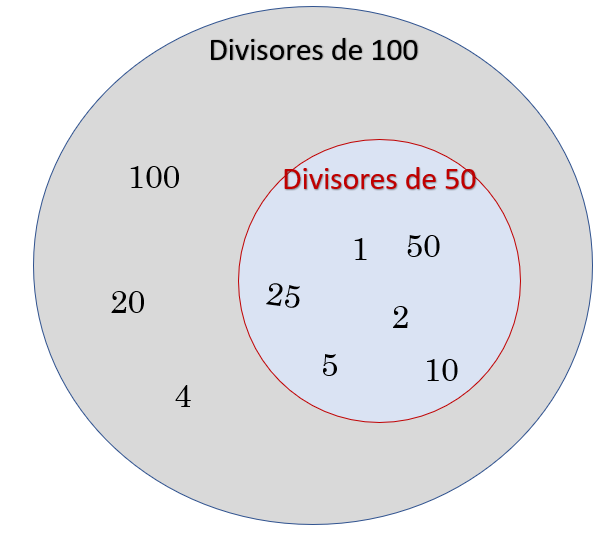
Ocurre lo mismo si divides 50 entre 4 no tienes un número entero, entonces, la respuesta en la tabla es “F” de falso.

Ahora, con base en este ejemplo, completa la tabla. Al final, quedaría de la manera siguiente:

En la columna de falso o verdadero, queda de la manera siguiente. Las dos primeras afirmaciones son falsas, en el caso de la primera afirmación, el número 6 representa el número total de libretas que hay en un paquete. Lo que lo hace ser el divisor de la cantidad total de libretas o de la cantidad de lápices de colores, también hay algunos argumentos, para otras afirmaciones que son falsas. Recuerda que siempre es importante que justifiques las respuestas que das.
Para finalizar recuerda que has trabajado con múltiplos y divisores comunes de dos o más números y es importante que hayas comprendido que los números que son múltiplos y divisores son números naturales o números enteros.
Estos conceptos te permiten dar solución a situaciones como la de encontrar la cantidad original de libretas o de lápices de colores.
Recuerda que los números naturales son los números que usas para contar, algunos ejemplos de situaciones que están implicadas con múltiplos, divisores, múltiplos comunes y divisores comunes son los horarios de toma de medicamentos, de salidas y llegadas de autobuses o diversas embarcaciones; la determinación del área o de algunas de las dimensiones de largo y ancho de superficies que se quieren recubrir.
El reto de hoy:
Revisa los ejercicios que realizaste y elige uno que puedas compartir con algún familiar cercano, explícale como pudiste obtener los resultados y pregúntale como lo habría resuelto, seguro le parecerá muy interesante.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm











Login to join the discussion