Los listones 2
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: convierte fracciones decimales a escritura decimal y viceversa. Aproximación de algunas fracciones no decimales usando la notación decimal.
Énfasis: expresa fracciones no decimales usando una aproximación representada con punto decimal.
¿Qué vamos a aprender?
En esta sesión vas a realizar la conversión de fracciones no decimales a escritura decimal.
Vas a necesitar tu libro Desafíos sexto grado, desafío 56, página 113, tu cuaderno u hojas para tomar notas, lápiz, goma, sacapuntas y mucha disposición.
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/113

¿Qué hacemos?
En esta sesión darás continuación a los desafíos 55 y 56. El desafío que se abordará es el 57, abre tu libro en la página 114, Listones 2.
En esta ocasión puedes observar la continuidad de un desafío con otro porque tienen el mismo título y con el 1 y el 2 queda señalada la continuidad. Revisa qué dice la consigna.

Consigna. Se tienen algunos listones de diferente longitud que deben ser cortados en partes iguales. En equipos, completen la tabla (recuerden dar el tamaño de las partes en metros).
Para trabajar con esta consigna debes preveer el material necesario que se menciona en la siguiente tabla. Observa los datos que presenta.

La imagen presenta una tabla de 4 columnas, la primera dice: Longitud del listón en metros, la segunda columna dice: Número de partes iguales en que se cortará el listón, la tercera columna dice, tamaño de cada una de las partes expresada como fracción en metros y la cuarta columna, tamaño de cada una de las partes, expresada con punto decimal en metros.
¿Recuerda a qué refiere la palabra longitud?
En este caso, longitud se refiere a lo largo de los listones.
En la primera columna se señala la longitud de cada uno de los listones que se van a recortar y la (m) que está entre paréntesis en los títulos de las columnas 1, 3 y 4, ¿Qué información nos brinda?
Es el símbolo de metro o metros; tanto para singular como en pural, se usa la “m” minúscula y sin punto.
Hace referencia a metros, la unidad de medida de la longitud; ¿Hay alguna otra palabra o símbolo que quizá no conozcas?
Empieza a trabajar con los listones. Como puedes observar en la columna uno y dos, se tienen los datos con los que vas a encontrar los valores o respuestas que completan las columnas tres y cuatro, de manera semejante a lo que se ha hecho en las actividades de los dos programas anteriores. En la columna uno, la primera longitud del listón que se tiene que cortar es de 10 metros, la segunda columna dice que lo vas a cortar en 3 partes iguales.
¿Para qué vas a cortar el listón? ¿Qué información se está buscando?
Se está buscando la medida que tendrán de largo las tiras de listón una vez que sean cortadas en el número de partes indicado, en la segunda columna.
Tienes que registrar esa información, la cual indica que debe expresarse en forma de fracción.
Entonces en la columna 3, ¿Van sólo fracciones?
Sí, pero ten presente lo que has venido haciendo con estos temas.
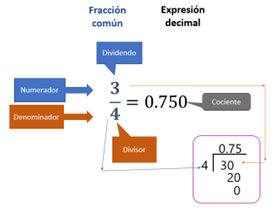
La fracción es una manera de expresar la división en la que el cociente corresponde a la expresión decimal de la medida del largo de las tiras resultantes, el numerador corresponde al dividendo y el denominador al divisor.
Observa cuál es la relación porque, desde la clase anterior, se hizo la división para encontrar la medida del largo de los listones.
Registra tus respuestas y argumentos a las preguntas que se vayan planteando, esto les ayudará a tener claridad acerca de lo que estás haciendo.
Inicia con el desafío, saca el listón previamente marcado en 3 partes iguales.
Hay un listón que mide 10 metros y se indica que hay que cortarlo en tres partes iguales. ¿Cómo hacer para que las partes salgan iguales, es decir, que tengan el mismo tamaño?
Lo puedes doblar en tres partes.
Ve doblando el listón, sólo que debes tomar en cuenta que las partes queden del mismo tamaño, ya realizado lo que se indica, en la primera columna debes escribir la fracción que exprese el tamaño de cada una de las partes.
Observa que el listón mide 10 metros. ¿Crees necesario que para encontrar el dato buscado, debas considerar la longitud del listón? Sí, porque se pide una fracción, como era un sólo un listón de 10 metros y se cortó en tres.
¿Cómo expresarías como fracción la longitud de cada parte? Registra en la columna 3
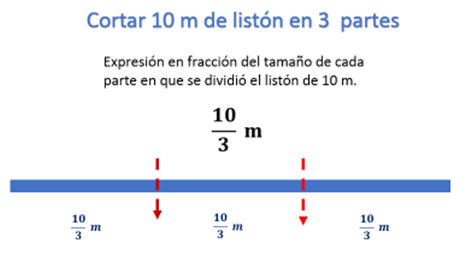
La longitud del listón completo es el numerador, 10 y el número de partes en que se divide es el denominador, 3 ¿Es diez tercios?
Diez tercios es la fracción común que expresa claramente la situación de división que estás haciendo y cada tramo de listón mide diez tercios de metro.
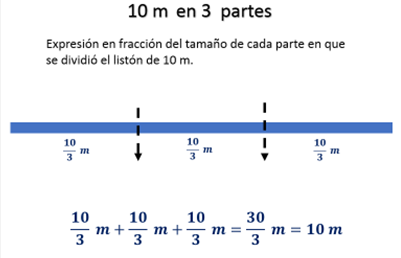
Sí, también se dijo que, si sumas la medida de los tres tramos debes obtener la medida del listón completo, así que tienes treinta tercios de metro que es equivalente a 10 m.
¿Crees que se puede encontrar una fracción equivalente para expresar la medida de cada tramo del listón?
3
13 ð‘š 13 m
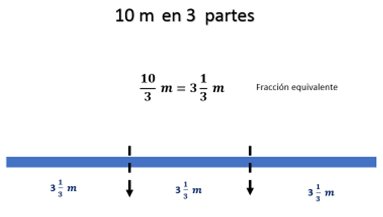
El tres cabe 3 veces en el 10, así que queda 3 metros con un tercio, encontraste un número que es equivalente para expresar la longitud de cada tira, tres metros y un tercio de metro. Este número tiene una parte entera y una fracción.
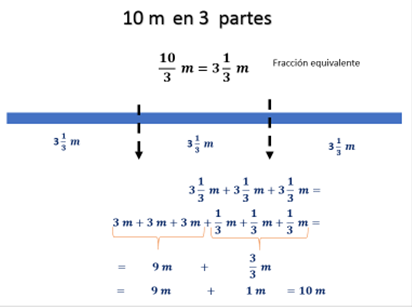
Esa expresión permite comprender que cada tramo mide más de un metro, o dicho de otra forma, el metro cabe tres veces más un tercio en cada tramo.
Al sumar la medida de la longitud de las tiras se observa que mide 10 metros.
Cada vez se conocen más formas distintas de expresar una misma cantidad. En particular, ahora lo que se hace con las fracciones y las expresiones decimales.
Ahora vas a buscar la respuesta que corresponde a la columna cuatro, donde indica que anotemos la expresión con punto decimal que representa la medida de la longitud de cada tramo.
Con la longitud del listón, 10 entre 3 partes que fue cortado, si tienes a la mano una calculadora, utilízala.

Da como resultado 3.333333
¿Cuántas cifras decimales tiene esa expresión decimal? ¿Cómo se puede leer?
Al oprimir la tecla igual, después de capturar la división diez entre tres, apareció tres enteros y después, en la parte decimal, muchos números 3 que llenaron la pantalla.
Eso se debe a que este tipo de expresión decimal se llama decimal periódico, no termina, siempre sigue dando 3 infinitamente.

De ahí, los puntos suspensivos que se escriben al final.
De acuerdo con lo que has estudiado, la expresión decimal es equivalente a la fracción común.
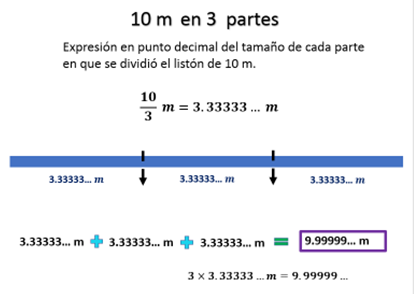
Sí, aunque en este caso, observa que al usar una expresión decimal periódica infinita, el resultado es aproximado. Como se identifica cuando usas la expresión decimal 3.3333… para indicar la longitud de cada uno de los tres tramos del listón de 10 metros de largo. Al sumar los tres tramos, obtienes como longitud total 9.99999… que es otra expresión decimal periódica infinita, también se puede observar si se considera la medida de longitud de un tramo y se multiplica por el número de partes, se obtiene la medida aproximada del listón.
Puede ser que hay quien consideró que era más exacta la expresión decimal, porque todo lo que tiene que ver con las fracciones podía ser más difícil. Incluso, por eso a las fraccione les llamaban quebrados, quebrados de cabeza.
Las fracciones permiten conocer la división original o de la que se parte, ciertamente, muchas personas prefieren usar la expresión decimal que la de fracción, sin detenerse a pensar cuándo es conveniente una u otra.
Por ejemplo, ¿Recuerdas que tres cuartos es equivalente a tres veces un cuarto?
34→3 ð‘£ð‘’ð‘ð‘’ð‘ 14→3 ð‘£ð‘’ð‘ð‘’ð‘ 0.250→0.750
De manera semejante, se puede decir que diez tercios es diez veces un tercio.
103→10 ð‘£ð‘’ð‘ð‘’ð‘ 13→10 ð‘£ð‘’ð‘ð‘’ð‘ 0.33333…→3.33333…
Hay más por conocer sobre las expresiones decimales equivalentes a las fracciones. Ahora se indica que este nuevo listón se corte en 6 partes iguales, así que comienza a doblar, deben quedar del mismo tamaño, ya está, ahora a cortar, listo, 1, 2, 3, 4, 5 y 6, todos quedaron del mismo tamaño.
¿Cuál es el tamaño expresado en forma de fracción de cada una de las partes?
Son 10 metros y seis partes,
106 ð‘š
, entonces aquí va 10 y abajo 6, quedando diez sextos de metro.
Ahora busca una fracción que sea equivalente a diez sextos.
Diez sextos es equivalente a cinco tercios:
106 ð‘š
=
53 ð‘š
Ya sabes qué ocurre con esa expresión decimal periódica, así que pasa a la última columna de este renglón, ¿Cómo encuentras la notación decimal que se acaba de expresar en fracción? ¿Ya sabes cómo? Con una división, por lo tanto, para encontrar la expresión decimal hay que dividir 10 entre 6

Lo cual da 1. 6666666 es importante tomar nota, regístralo en tu cuaderno, porque lo vas a usar más adelante.
Aquí va 1.66666666… ya se verificó y al dividir cinco entre seis también es 1.666…

Analiza los datos de la siguiente división, ahora el listón tiene una longitud menor a la de los dos anteriores, utiliza lo que se ha estudiado hasta aquí para que contestes este renglón y el siguiente de la tabla.
Para verificar sus respuestas pueden utilizar los listones o las tiras de papel de la manera en que se ha hecho.
También observa los datos que se obtuvieron hasta este momento. Analiza la tercera columna, ¿Ya observaste los 4 datos? ¿Se parecen o son diferentes? ¿Qué notaste?

En este caso, se observa que los datos del primer y tercer renglón indican el mismo número de partes iguales en que se cortará el listón, como ocurre con el segundo y cuarto renglón que indica dividir entre 6
Ahora, observa qué sucede al dividir un listón que mide 5 metros de longitud, en siete partes.
Dobla el listón en siete partes iguales y corta, analiza los resultados que vayas obteniendo.

Para la expresión en fracción hay que expresar 5 metros en siete partes iguales, o sea cinco séptimos.
¿Se podrá buscar una fracción equivalente menor a 5 séptimos?
¿Encontraste alguna fracción equivalente que se pueda representar con cifras menores que cinco séptimos?
No, esa fracción ya no se reduce más, cinco séptimos es irreducible.
Ahora, considera cómo obtendrías la expresión decimal de cinco séptimos, ¿Qué tipo de expresión decimal crees que tenga?
Es decir, ¿Es un número decimal exacto o una expresión decimal periódica?
Considerando que el número de partes en que se va a dividir es mayor que la longitud del listón, la longitud de cada tramo es menor que la unidad de medida.
Analiza lo que puede llegar a representar una fracción. ¿Cuánto mide cada uno de los siete tramos en que dividieron los cinco metros de listón en forma de expresión decimal?
Usa la calculadora para dividir 5 entre 7 y encontrar la expresión decimal de cinco séptimos.
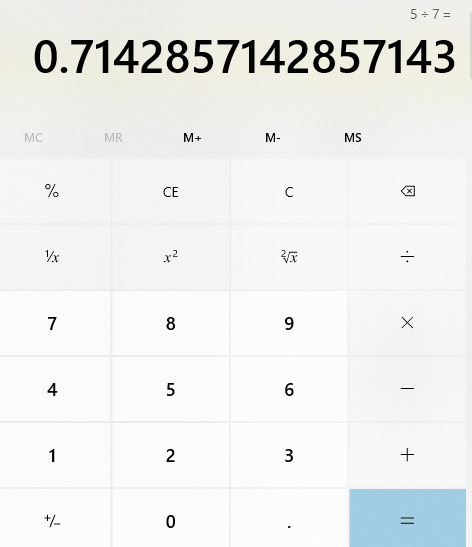
Como resultado 0.714285714285 y otra vez se repiten las cifras 714285… En este caso, ¿Cómo es conveniente escribirlo?
En casos como éste solamente se anotan las cifras hasta donde se identifique que vuelven a repetirse.
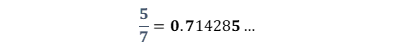
Quedando así la expresión decimal de cinco séptimos como: cero punto siete uno cuatro dos ocho cinco y puntos suspensivos.
Como pudiste darse cuenta, al expresar la medida de la longitud de los tramos de listón puede ocurrir que la expresión decimal sea exacta, o bien, que sea periódica.
Cuando la expresión decimal de la longitud de una tira es periódica significa que al multiplicar por el número de partes que se cortaron es aproximadamente igual que la medida de la longitud total de la tira, pero no es la misma.
Observa el siguiente video y tomar notas para tener presente este aprendizaje.
-
Video. Tipos de fracciones y decimales.
El reto de hoy:
Comparte con alguien cercano, lo que aprendiste de las fracciones y su expresión en números decimales. Explícale con alguno de los ejercicios realizados con los listones, seguramente le quedará muy claro y le parecerá muy interesante.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm
Descarga tu clase dando clic aquí



Login to join the discussion