La sucesión en práctica
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: identificaca y aplica de la regularidad de sucesiones con números (naturales, fraccionarios o decimales) que tengan progresión aritmética o geométrica, así como sucesiones especiales. Construcción de sucesiones a partir de la regularidad.
Énfasis: construye sucesiones con progresión aritmética, geométrica y especial, a partir de la regla de formación.
¿Qué vamos a aprender?
Aprenderas a identificar y aplicar la regularidad de sucesiones con números (naturales, fraccionarios o decimales) que tengan progresión aritmética o geométrica, así como sucesiones especiales. También podrás realizar la construcción de sucesiones a partir de la regularidad y construir sucesiones con progresión aritmética, geométrica y especial, a partir de la regla de formación.
¿Qué hacemos?
Para empezar revisa la carta de la niña Dulce Valeria de la Primaria Manuel Borja Soriano que encontró una sucesión y desea que todos y todas analicemos.

Ahora observa qué operaciones hizo Dulce Valeria para encontrar los términos de la sucesión.
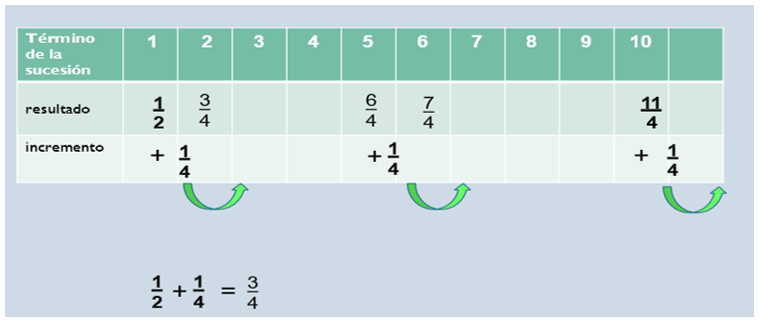
Como puedes observar, dice que esta sucesión se genera al sumar un cuarto; entonces Dulce Valeria sumó un medio más un cuarto para obtener el segundo término de la sucesión que es 3 cuartos, y los demás términos son fáciles de obtener. ¿Tú cómo lo habrías resuelto?

También observa cómo se expresa la sucesión con números decimales.
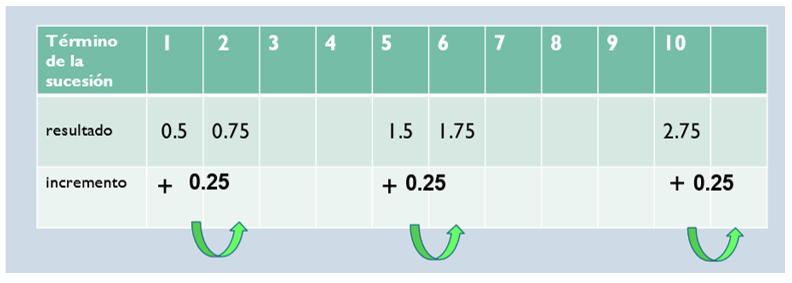
Ahora observa qué hizo Dulce Valeria. Ella anotó cinco décimos que, como sabes, es equivalente a un medio, y un cuarto es equivalente a veinticinco centésimos. Ahora los términos de la sucesión en la tabla van incrementando de veinticinco centésimos en veinticinco centésimos. Para obtener el segundo término hay que sumar a cinco décimos, veinticinco centésimos y obtenemos setenta y cinco centésimos.
Parece que Dulce Valeria tuvo muchas estrategias muy buenas para generar las sucesiones que le pidieron. Sí comprendió cómo generar una sucesión con las condiciones que le daban.
Bueno, ahora revisa el problema 3 de la página 115 de su libro de Desafíos matemáticos.
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/115

El problema 3 es el siguiente:

Ahora analiza qué estrategia podría ser la mejor para resolver este desafío. Busca una forma que te permita resolverlo.
¿Te parece ver si conviene convertir a decimales o conviene usar fracciones? ¿Qué piensas?
La notación decimal de un tercio, es 0.3333
13=0.333
y le puedes sumar 0.5 ¿Y qué términos se obtienen?
Pues el primero es 0.3333, el siguiente es 0.8333, el tercero es 1.3333, el cuarto es 1.8333, el quinto es 2.3333, observa que siempre queda ese número decimal infinito.
Así es, el número que cambia es el de los décimos y los enteros, pero, ahora realiza la sucesión con fracciones.
Puede ser más complicado, porque 5 décimos es lo mismo que un medio y sumar medios con tercios, no se puede hacer directamente. Efectivamente, pero sabes que siempre se pueden convertir las fracciones en otras equivalentes que sean fáciles de sumar.
Si conviertes en sextos las dos fracciones, la obtención de los términos es mucho más sencilla. Observa, ¿A cuántos sextos equivale un medio? Equivale a 3 sextos y un tercio es equivalente a 2 sextos.

Una vez que ya se tiene el mismo denominador, la suma es mucho más sencilla. El primer término de la sucesión sería un tercio o podrías poner también dos sextos, pues representan la misma cantidad. ¿Cuál sería el segundo término?
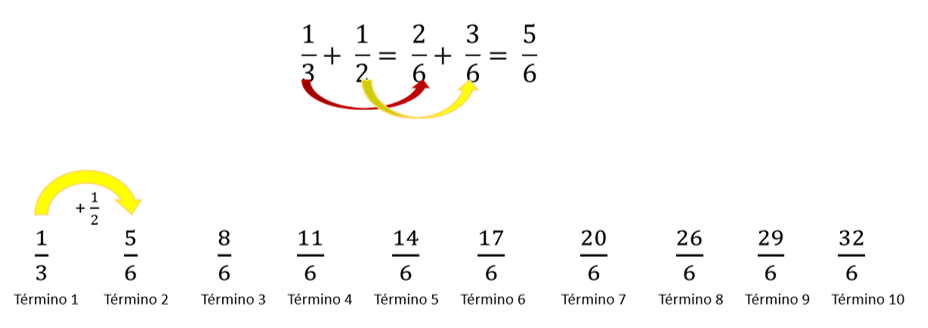
Dos sextos más tres sextos son 5 sextos, la tercera es 8 sextos, la cuarta es 11 sextos, luego 14 sextos. ¿Ya viste qué fácil es también encontrar los términos de una sucesión con fracciones?
Parece interesante ver la manera en que se usan las diferentes expresiones de un número, por ejemplo, usar fracciones equivalentes o usar su expresión como número decimal y la forma en que se pueden aplicar estrategias para encontrar el resultado deseado.
Considera que al buscar información sobre las sucesiones puede encontrarse un enlace donde hay estudiantes de diversas escuelas de sexto grado que están practicando matemáticas en un club. Es muy interesante, es el club de los genios matemáticos. Los alumnos y las alumnas de sexto grado ponen retos en los que practican matemáticas y sobre todo ellos se ponen retos para jugar y aprender.
En este club pusieron como reto una sucesión para que la resolvieras aquí.

La sucesión se inicia con el número 12 y se multiplica por dos para generar el siguiente término. Puedes observar que cada término va aumentando el doble del anterior. Los primeros seis términos de la sucesión, son: doce, veinticuatro, cuarenta y ocho, noventa y seis, ciento noventa y dos, trescientos ochenta y cuatro. La pregunta es, si en lugar de iniciar con 12 se inicia con 1.2 y la regla es multiplicar por dos. ¿Cuáles son los primeros seis términos de la sucesión?
Puedes apoyarte con la calculadora para encontrar los términos que piden.
Entonces el primer término será 1.2 pero tendrás que multiplicarlo por 2 para obtener el segundo término que es 2.4, el tercer término es 4.8, ¿Qué curioso? En la primera sucesión tenemos 12, 24 y 48 en la segunda sucesión están 1.2, 2.4 y 4.8, son las mismas cifras que en la primera sucesión, pero el punto decimal está entre ambas cifras.
¿Quieres continuar para ver si eso ocurre con los siguientes tres términos de esta segunda sucesión?

Entonces ahora, multiplica por dos a cuatro enteros ocho décimos y es nueve enteros seis décimos, también coinciden, y luego esto por 2 y son 19 enteros con 2 décimos y el último por 2 salió 38.4
¿Por qué crees que se parezcan tanto la primera sucesión y la segunda? ¿Tienes alguna respuesta? ¿Habrá alguna relación entre ambas sucesiones o fue mera coincidencia? ¿Qué opinas?
Observa, las dos tienen la misma regularidad, que es multiplicar por 2, y una comienza con 12 y la otra con 1.2 ¿Qué relación puede haber entre estos números? ¿Qué le harías al 12 para convertirlo en 1.2? Si divides 12 entre 10, el resultado es 1.2

Eso que hiciste con el 12 para obtener 1.2 ¿Es lo mismo que se puede hacer con los términos de la primera sucesión? Realiza las operaciones en la calculadora. El segundo término de la primera sucesión es 24 y en la otra da 2.4 en este caso sí se cumple, porque si divides 24 entre 10, da 2.4 observa el siguiente término 48 entre 10, son 4.8, ya te diste cuenta que es verdad con los demás también se cumple que cada término de la segunda sucesión es la décima parte de los términos de la primera sucesión.
Entonces, puedes considerar los otros términos de la primera sucesión y generar los de la segunda sucesión, sabiendo que 1.2 es la décima parte de 12 y que la regularidad en ambas sucesiones es la misma.
Nuevamente estás usando una relación entre los números para obtener los términos de la sucesión.
En el siguiente desafío lo podrás verificar. Ve al problema 4

Usa la calculadora o si lo prefieren, realiza las operaciones escritas. ¿Recuerdas que ayer trabajaste con una sucesión cuyo patrón entre un término y el siguiente era una multiplicación? Bueno, ésta que se propone en el desafío, también dice que para pasar de un término al siguiente debes multiplicar.
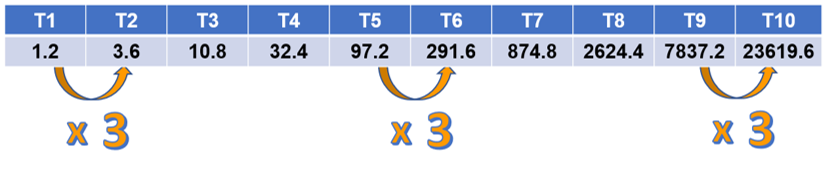
Parte de uno punto dos y este número se multiplica por tres, así obtienes el segundo término que es 3.6, ahora vuelve a multiplicar por 3 y da 10.8, otra vez por 3 y da 32.4, otra vez por 3 y da 97.2, otra vez por 3 y da 291.6, otra vez por 3 y da 874.8, otra vez por 3 y da 2624.4, otra vez por 3 y da 7873.2, otra vez por 3 y el décimo término es 23619.6
¿Te diste cuenta cómo crecen los términos de usa sucesión como ésta, donde la regularidad consiste en multiplicar?
Siguiente desafío.

Esta sucesión es muy interesante, ¿Ya te diste cuenta que no se forma como las que has visto hasta ahora? Has visto sucesiones donde la regularidad ha sido sumar un número constante, un término para obtener el que sigue, también viste otras donde hay que multiplicar un número constante a los términos para obtener los siguientes.
Observa, ya te dieron los primeros 4 términos de la sucesión y piden que encuentres los 5 que siguen con una regla especial que consiste en sumar al número anterior, el número de la posición del que vas a escribir.
Analiza bien lo que tienes y lo que te indican, dice que la sucesión comienza con 1, pero que el 3, que es el segundo término, se obtuvo de sumar 1 más 2, que es la posición que ocuparía el 3, ¿Verdad?
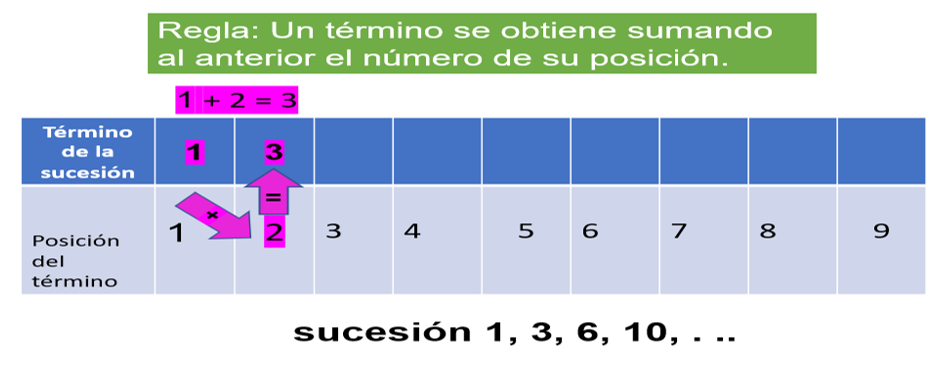
Recuerda que, en una sucesión, es muy importante el orden en que se dan los términos que la forman. Quiza te resulte más sencillo si usas un esquema.
Aplicando la regla: “Un término se obtiene sumando al anterior, el número de su posición”. Vas a identificar los términos de la sucesión, son: 1, 3, 6 y 10 enseguida, identifica su posición 1, 2, 3 y 4
Entonces, para calcular el término en la segunda posición debemos realizar la suma del número anterior, que es uno y la posición, que es dos, esto es:
1 + 2 = 3
Queda claro lo que debes hacer, ¿Puedes calcular otro término?
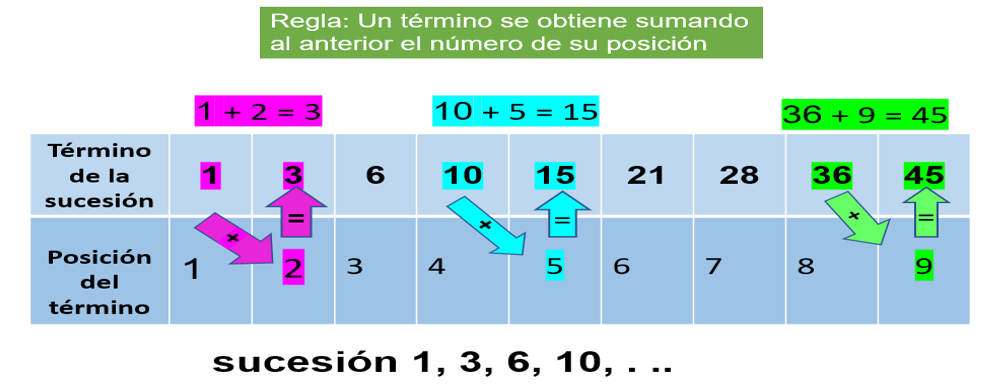
El siguiente término, ¿Qué posición ocupará? Pues, ocupará el lugar 3 y le debes sumar el número anterior que fue 3, por eso es 6
Y el número siguiente ocupará el lugar 4 que sumado al 6 anterior, nos da 10, que ya tienes aquí; ahora hay que determinar cuáles son los 5 términos que siguen. Así es, ahora hay que sumar la quinta posición con el 10, entonces el siguiente término será 15
Y el hacer los esquemas te ayuda mucho, porque vas analizando lo que debes hacer para pasar de un término a otro.
Ahora determina cuáles son los 5 términos que siguen a la sucesión que acabas de ver. Al concluir observa el video siguiente:
-
Video. Reglas de sucesión.
https://www.youtube.com/watch?v=9hN2j-064uM
¿Te fijaste que además de recordarnos cómo se puede obtener una sucesión donde se suma un número constante, también invita a pensar en cómo saber qué término ocupa un lugar muy alejado de la sucesión? ¿Qué se te ocurre que se podría hacer?
El reto de hoy:
Pónle un reto a alguno de tus familiares, marca una línea de sucesión de números y pregúntale qué número sigue, ya que te de sus respuestas, pídele que te explique por qué considera esos resultados y de estar correctos felicítalo o felicítala y, si no son correctos, explícale por qué.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm
Descarga tu clase dando clic aquí



Login to join the discussion