Partes de una cantidad
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: resuelve problemas que impliquen calcular una fracción de un número natural, usando la expresión “a/b de n”.
Énfasis: relaciona el cálculo de n/m partes de una cantidad con la multiplicación y la división.
¿Qué vamos a aprender?
Aprenderas a resolver problemas que impliquen calcular una fracción de un número natural, usando la expresión “a/b de n”, para hacerlo relacionarás el cálculo de n/m partes de una cantidad con la multiplicación y división.
¿Qué hacemos?
Para iniciar es importante que reconozcas que aun en pleno 2021 existen muchas personas que no saben leer, ni escribir debido a que no tuvieron la oportunidad de acudir a la escuela por diversas circunstancias.
Por ejemplo, los abuelitos de la maestra Laura, nacieron en 1913 y 1914 dice que su abuelito Adolfo no sabía leer, ni escribir y se le dificultaban las operaciones matemáticas, sin embargo, su abuelita Manuela, sí sabía y ella lo ayudaba. Los recursos económicos que cada uno tenía cuando fueron niños, marcaron la diferencia que había entre ellos.
Los padres de la abuelita si tenían dinero para enviarla a una de las pocas escuelas que había en ese momento o para pagar alguna persona que les pudiera enseñar y el abuelito no, él era huérfano y tenía que trabajar.
Los abuelitos nacieron hace más de 100 años, quizá ya casi no hay personas analfabetas.
|
|
|
¿Habrá gente más joven que la abuelita de la maestra Laura, que no sepa leer y escribir en la actualidad?
Aunque las circunstancias eran diferentes hasta no hace muchos años, observa lo que pasa actualmente. Para ello visita la página CUENTAME del INEGI donde existe información para niños. Hay información que se ha recabado en los censos, el último fue realizado en el 2020 identifica la información que tiene sobre el analfabetismo.
Aunque en el país la educación básica (preescolar, primaria y secundaria) cada vez llega a más lugares, muchos jóvenes, por diversas razones, no asisten a la escuela y por lo tanto, algunos de ellos no saben leer ni escribir.
Analfabeta(o): Es la persona de 15 o más años de edad que no sabe leer ni escribir un recado.
En México, durante los últimos 50 años, el porcentaje de personas analfabetas de 15 y más años bajó de 25.8 % en 1970 a 4.7 % en 2020 lo que equivale a 4,456,431 personas que no saben leer ni escribir.
De las personas que no saben leer ni escribir actualmente según esta información, ¿De qué edad estimas que sean en su mayoría?
Observa la siguiente información que hay en esta página.

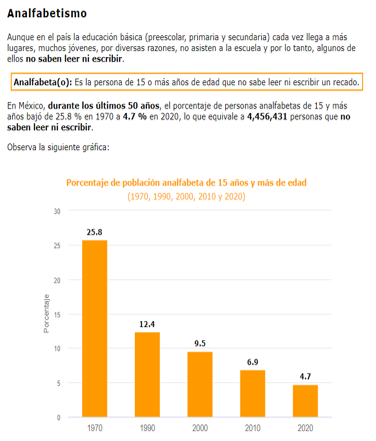
Por sexo. De acuerdo con el Censo de Población y Vivienda 2020 cuatro de cada 100 hombres y seis de cada 100 mujeres de 15 años y más no saben leer ni escribir.
Hay quien piensa que sólo habría personas de mayor edad que no supieran leer ni escribir, pero según esta información, también hay jóvenes de 15 años que no saben leer ni escribir, existen diversas circunstancias que provocan esta situación.
Analiza desde las matemáticas esta información, decir 4 de cada 100 hombres de 15 años y más, no saben leer ni escribir es una razón, de acuerdo con lo que has aprendido en otros programas.
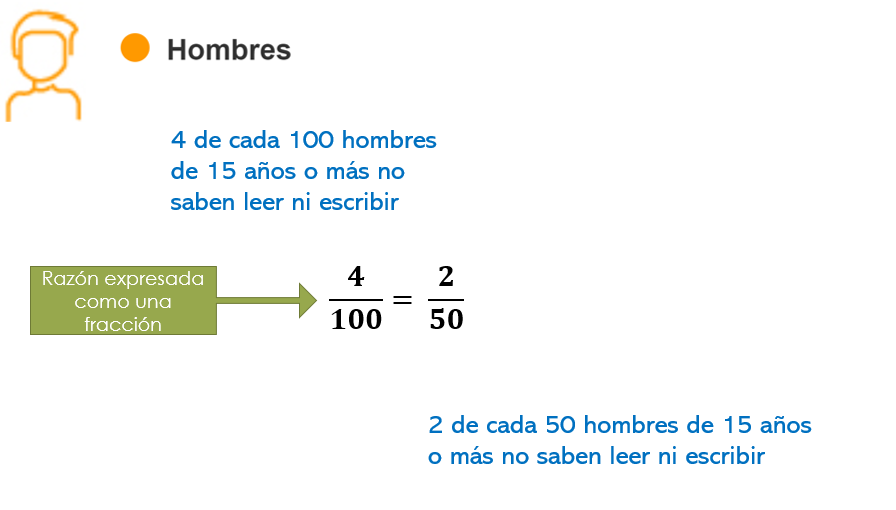
Recuerda que se puede expresar como una fracción, esto es cuatro centésimos. Además, si se reduce observa que es equivalente a la fracción dos cincuentavos, lo cual se interpreta como 2 de cada cincuenta hombres de15 años y más, no saben leer ni escribir.
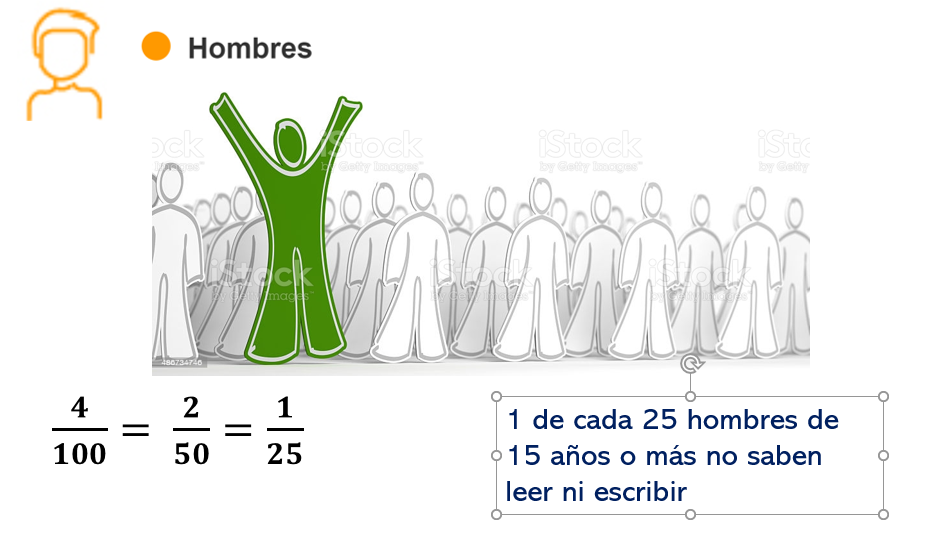
Se puede reducir aún más si le sacas mitad a la fracción dos cincuentavos, entonces queda un veinticincoavo.
¿Qué interpretación tendría en la situación que se está investigando?
¿Será uno de cada veinticinco hombres?
Significaría que de un grupo de veinticinco hombres de 15 años o más, uno de ellos no sabe leer ni escribir.
Increíble, pero cierto, por cada grupo de 25 hombres, uno de ellos no sabe leer y escribir, entonces, ¿Cuántos hombres de 15 años o más no saben leer ni escribir en total en México?
Habría que seguir investigando algunos datos más, por ejemplo, cuántos hombres de 15 años y más hay en el país y de ahí podrías calcularlo aplicando la razón o fracción que obtuviste.
Observa este dato: la población de hombres mayores de 15 años y más es de 45 millones, 252 mil, 363 esa cantidad demuestra que si son muchos los hombres que por alguna razón no saben leer ni escribir.
Hoy conocerás algunas estrategias que te permitirán hacer cálculos para saber cuántos hombres de 15 años y más están en esa condición, de acuerdo con el censo 2020
Así que es momento de empezar con el libro de texto. Localza la página 117 Desafío 60, Partes de una cantidad.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/117

Como lo menciona la consigna, analiza la información que presentan los problemas que integran este desafío.
Problema 1. En un grupo de 36 alumnos, un tercio del total son menores de 10 años.
¿Cuántos tienen 10 o más años?
¿Qué parte del grupo tiene 10 o más años?

Considera la información que presenta el problema e imagina a un grupo de 36 personas en las que hay personas menores de 10 años y mayores que 10 años, de acuerdo con lo que indica el problema. ¿Qué observan? ¿Qué relaciones encuentran entre los datos?
Dice un tercio del total son menores de 10 años quiere decir que 1 de cada 3 estudiantes son menores de 10 años.
Esa es la razón que corresponde a la fracción un tercio, en esta situación. ¿Cómo podrías representar esta información gráficamente?
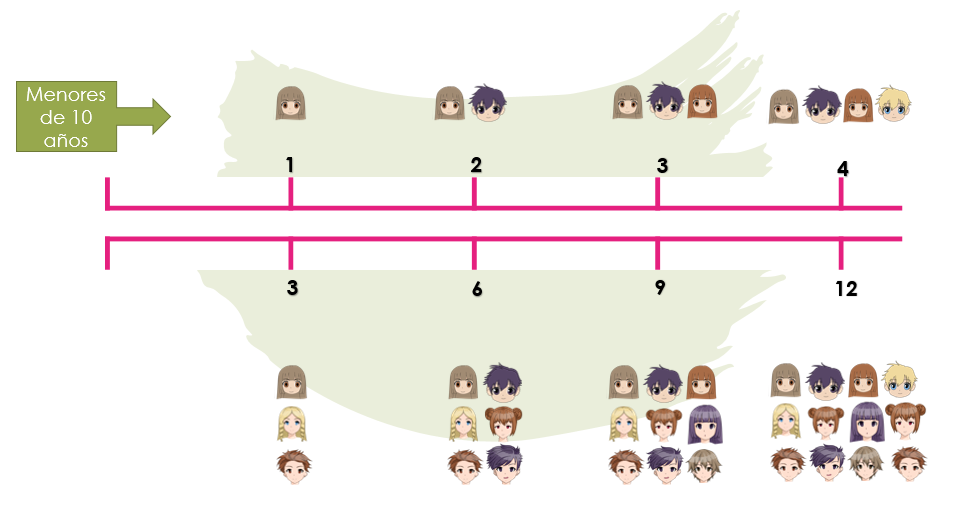
De esta manera puedes identificar que son 4 estudiantes de 12 menores de 10 años y así continuarías.
A partir de la representación gráfica de la razón: 1 de cada 3 estudiantes son menores de 10 años, encuentras diferentes pares de grupos de estudiantes que corresponden con esa razón y que también representan la fracción, un tercio.
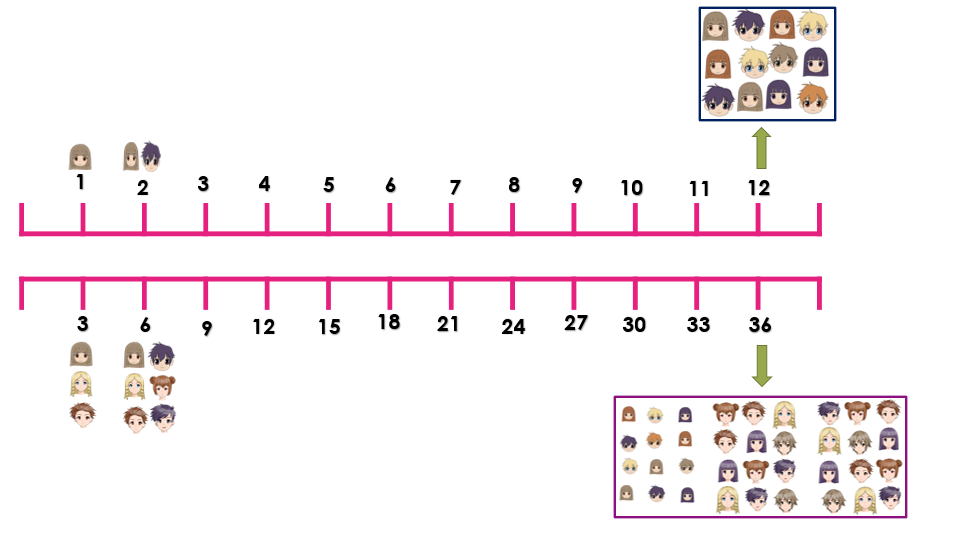
Aplicando la propuesta, aumentó de manera proporcional y se llegó a 12 estudiantes de 36 son menores de 10 años.
Como puedes observar, se fueron aumentando las cantidades de forma proporcional hasta que se encontró el 36 que es el total de estudiantes del grupo que menciona el problema.
Entonces, ya sabes que 12 alumnos de 36 son menores de 10 años. Ahora, ¿Cómo usar esta información para saber cuántos estudiantes tienen 10 o más años?
Se puede saber restando 12 a 36: 36 – 12 = 24
Observa, treinta y seis menos doce es igual a veinticuatro. Eso significa que veinticuatro estudiantes tienen 10 o más años en ese grupo de treinta y seis estudiantes.
Esta es otra manera de obtener el resultado, cada quien va encontrando distintas estrategias y formas para llegar al resultado.
Conoce otra estrategia más, observa, qué sucede si se interpreta un tercio de 36 estudiantes son menores de 10 años como la división de treinta y seis estudiantes entre tres.

Así se obtienen tres grupos de 12 estudiantes, uno de cuales es el de los estudiantes menores de 12 años, y los otros dos grupos de 12 estudiantes tienen 10 años o más.
Observa que se encontraron las dos cantidades que se necesitan para dar respuesta a la pregunta; un tercio que son 12 niños menores de 10 años y 24 de 36 estudiantes tienen 10 o más años.

A través de la división también se puede llegar a la respuesta de la pregunta que se plantea en el libro, ¿Cuántos estudiantes tienen 10 o más años?
Podrías escribirla como fracción
2436
estudiantes tienen 10 años o más.
De esta manera, se pueden buscar fracciones equivalentes hasta llegar a su mínima expresión, es decir, donde ya no se puedan reducir más. Así que empieza por dividir a la mitad o entre 2

Se obtiene la mitad de 24 y 36 y es 12 de 18 también puedes sacar mitad y queda 6 de 9 y ya no se puede sacar mitad.
Piensa en un número que divida exactamente al 6 y al 9 y es el 3, 6 entre 3 = 2 y 9 entre 3 = 3 por lo tanto, 2 tercios es la parte del grupo que son estudiantes de 10 años o más.
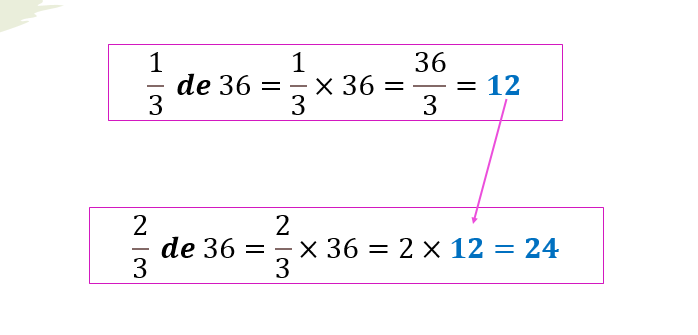
¿Te diste cuenta de que, al tener un tercio de 36 faltan dos tercios para completar el entero? Entonces, al dividir 36 entre 3 y multiplicar los 12 estudiantes que representaban un tercio por dos, obtuvieron como resultado 24 alumnos que son los dos tercios restantes.
Observas, así también así se puede resolver.
Es importante resaltar que para conocer qué parte de una cantidad es una fracción de ella, puedes dividir y multiplicar sucesivamente esa cantidad. Divide entre el denominador y multiplica por el numerador de la fracción.
Ahora trabajacon el problema 4

Problema 4. En la zona escolar hay 15 escuelas a las que asisten en total 3 760 alumnos, de los cuales 2 820 tienen más de dos hermanos. ¿Qué parte del total de alumnos tiene dos hermanos o menos?
Analiza la información que proporciona el problema:
15 escuelas.
3 760 estudiantes en total.
2 820 tienen más de 2 hermanos.
¿Qué parte del total de alumnos tiene dos hermanos o menos?
Una estrategia podría ser que se determine la razón entre el número de estudiantes que tienen dos hermanos y el total que hay en las 15 escuelas. Esto sería 2820 tienen más de dos hermanos de 3760 alumnos que hay en total.
2 8203 7602 8203 760
La relación que se presenta es correcta, hay que pensar cómo se puede utilizar para encontrar qué parte representa 2820 de 3760. Hay que buscar una fracción, un medio, o un tercio o un cuarto, según aplique.
Por ejemplo, en el problema anterior que acabas de resolver, la razón era que uno de tres o un tercio del total del grupo, eran menores de 10 años, y se buscaba una cantidad de estudiantes de 10 años o más.
Este problema puede verse al revés, dan las cantidades y hay que buscar las razones o fracciones.
Por eso es importante buscar que parte es 2820 de 3760 estudiantes.
Quizá hacer una división, pudiera ayudar a obtener el resultado.
Dibuja en tu cuaderno una tabla de dos columnas y cuatro filas.
En la primera fila, anota a la izquierda el número 1 y en la celda de la derecha, el total de los alumnos 3760
¿Sabes por qué te solicitan escribir el número 1?
Es uno porque la cantidad de estudiantes es el total, o sea, la unidad.
Con esto, ¿Ya te diste una idea de cómo se puede resolver el problema?
Puedes comenzar por dividir la cantidad.
¿Cómo aplicar la división? Puedes hacerlo con la calculadora y ve registrado los datos que obtengas.
Divide 3760 entre 2 lo cual te da 1880
Registra en la primera columna 1880 ¿Qué parte es 1880 de 3760?
Es un medio.
Registra un medio en la tabla, en la celda derecha.
Divide 1880 también entre 2 y te da 940
Registra 940
940 representa una cuarta parte de todos los niños.
Anota en la tabla, un cuarto.
Este dato sí sirve para lo que se necesita.
Al hacer una pequeña estimación con el 900 sucede que 900 por 3 es igual a 2700
Por tanto se encuentra que un cuarto de 3760 son 940 ¿Cómo se puede comprobar si es el dato que se necesita para encontrar la respuesta al problema?
Si multiplicas 940 por 2 da lo mismo que un medio = 1880 pero si multiplicas 940 por tres da: 2820 que es el número de niños que tienen 2 o menos hermanos.
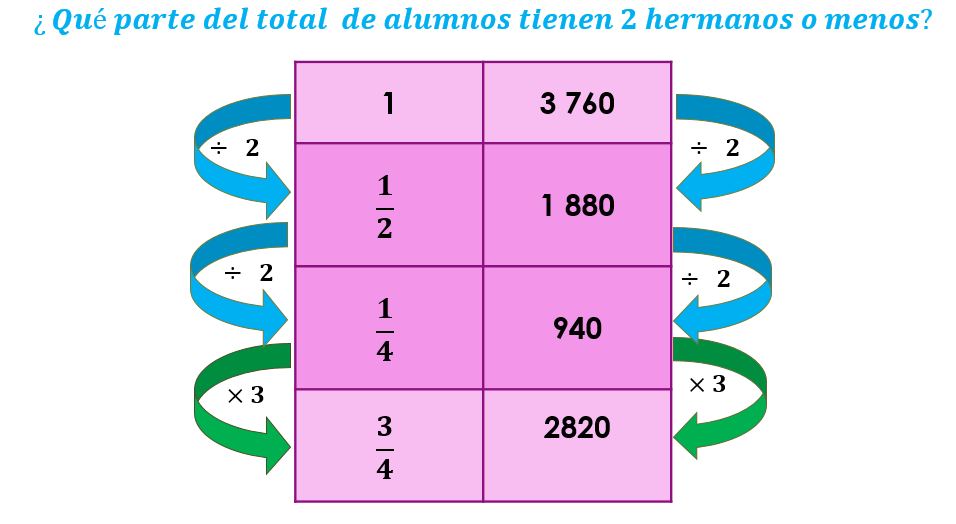
Observa la siguiente imagen que tiene lo que se acaba de hacer: al dividir la cantidad total de los alumnos, que es de 3760 en cuartos, es decir en 4 partes, obtienes que un cuarto de 3760 es 940 y si esta cantidad la multiplicas por tres y obtienes 2820 por lo tanto 3 cuartos de 3760 estudiantes son los que tienen dos hermanos o menos.
Hay otra forma de llegar a esa respuesta, ¿Cuál podría ser?
Prueba a dividir 2820 entre 3760 y registra ¿Qué obtienes?
El resultado es 0.75 que es equivalente a 3 cuartos también.
Esa es otra forma de obtener la respuesta. ¿Podrías calcular cuántos hombres de 15 años o más no saben leer ni escribir?

La población total de hombres mayores de 15 o más años es de 45 millones, 252 mil 363 y de ellos una veinticincoava parte no sabe leer ni escribir.

Son un millón 810 mil 095, hombres de 15 años o más que no saben leer ni escribir.
Sí que son muchas personas porque además falta considerar a las mujeres que están en esta misma condición.
El reto de hoy:
Investiga cuántas mujeres hay en México, de 15 años o más y cuántas de ellas no saben leer ni escribir. Comparte el trabajo realizado con algún familiar y explícale como resolviste los problemas, seguramente le parecerán muy interesantes y útiles.
Si en tu casa hay libros relacionados con el tema, consúltalos, así podrás saber más.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm
Descarga tu clase dando clic aquí





Login to join the discussion