¿Cuánto suma?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: resuelve problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura de los problemas. Estudio o reafirmación de los algoritmos convencionales.
Énfasis: resolver problemas aditivos con números decimales y fraccionarios utilizando los algoritmos convencionales.
¿Qué vamos a aprender?
Resolverás problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura de los problemas.
Para explorar más sobre el tema, puedes consultar el libro de texto de Desafíos Matemáticos de 6º, se explica el tema a partir de la página 15.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/15
Determinarás problemas aditivos con números decimales y fraccionarios utilizando los algoritmos convencionales.
¿Qué hacemos?
Revisaremos los problemas con sumas y restas de números fraccionarios y decimales de los desafíos 6 y 7 de tu libro de texto, que tienen por título “Vamos a completar” y “Rompecabezas” y se encuentran en las páginas 15 a 18.
Los desafíos que trabajamos se parecen a muchas de las situaciones de la vida real en que usamos las Matemáticas, en las que debemos utilizar nuestra imaginación, nuestra intuición y nuestro ingenio.
Realizarás algunas actividades parecidas a las que ya hicimos en esos desafíos, para reafirmar tu capacidad de utilizar algunas estrategias que fuimos descubriendo al resolverlos.
Comenzaremos con algunas actividades que se refieren a las sumas y restas de fracciones. Lee la consigna.
-
¿En cuánto excede 8/11 a 3/5?
La palabra “exceder” significa “ser más grande” o “ir más allá del límite”. Por eso, se te pide calcular por cuánto es más grande 8/11 en comparación a 3/5.
Realiza en tu cuaderno la operación y resaltan la búsqueda de un denominador común por medio de la multiplicación de los denominadores originales.
En secundaria aprenderás a buscar el mínimo común múltiplo para no tener que trabajar siempre con denominadores tan grandes. A veces, el mínimo común múltiplo es la multiplicación de los denominadores originales, como los de esta operación. Sin embargo, en algunos casos es posible simplificar las fracciones antes de comenzar por la suma o la resta para trabajar con números más chicos.
Leer la siguiente consigna.
-
Comprobar que 9/12 + 2/4 = 1 2/8
Sólo tienes que realizar la suma de fracciones para comprobar que el resultado es el que ahí nos dan. Aunque la multiplicación de los denominadores nos puede dar números grandes.
Puedes simplificar las fracciones que están en la operación antes de llevarla a cabo; para cada una, podemos dividir el numerador y el denominador por un mismo número. ¿Te das cuenta cuál nos puede servir para cada una?
Hacer la simplificación de fracciones y llegar a la expresión 3/4 + 1/2 = 1 1/4. Resuelven la operación mediante el algoritmo convencional. De manera opcional, descubren que 1/2 es igual a 2/4, y que este denominador les puede facilitar la operación.
Las Matemáticas requieren que prestes atención a los detalles, y de vez en cuando se te pueden pasar algunos. Por eso, el intercambio de puntos de vista con alguien que nos revisa es de utilidad, no sólo para no equivocarte, sino para seguir aprendiendo.
¿Vemos la siguiente consigna?
-
¿Qué número sumado a 6/8 da como resultado 1 9/15?
Aquí ya nos hablan de una suma que puede realizarse, pero que está incompleta, te falta encontrar a uno de los sumandos. ¿Qué tenemos que hacer?
Tenemos que restar 1 9/15 meno 6/8 para encontrar el número faltante. También aquí podemos simplificar antes de hacer la operación.
Realiza la simplificación de los elementos de la resta, llegando a 1 3/5 y 3/4. Después, has la resta siguiendo el algoritmo convencional.
Recuerda que la regla principal consiste en multiplicar los denominadores para encontrar un denominador común que te permita hacer la suma o la resta de fracciones que necesitamos.
Veamos la siguiente consigna, antes de pasar a resolver algunas actividades con números decimales.
-
¿Qué tanto es menor o mayor a 2 la suma de 5/6 y 4/5?
Para repasar los problemas de sumas y restas con decimales, vamos a realizar una actividad parecida a la primera consigna del desafío 7, “Rompecabezas”. Página 17 de tu libro de texto.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/16
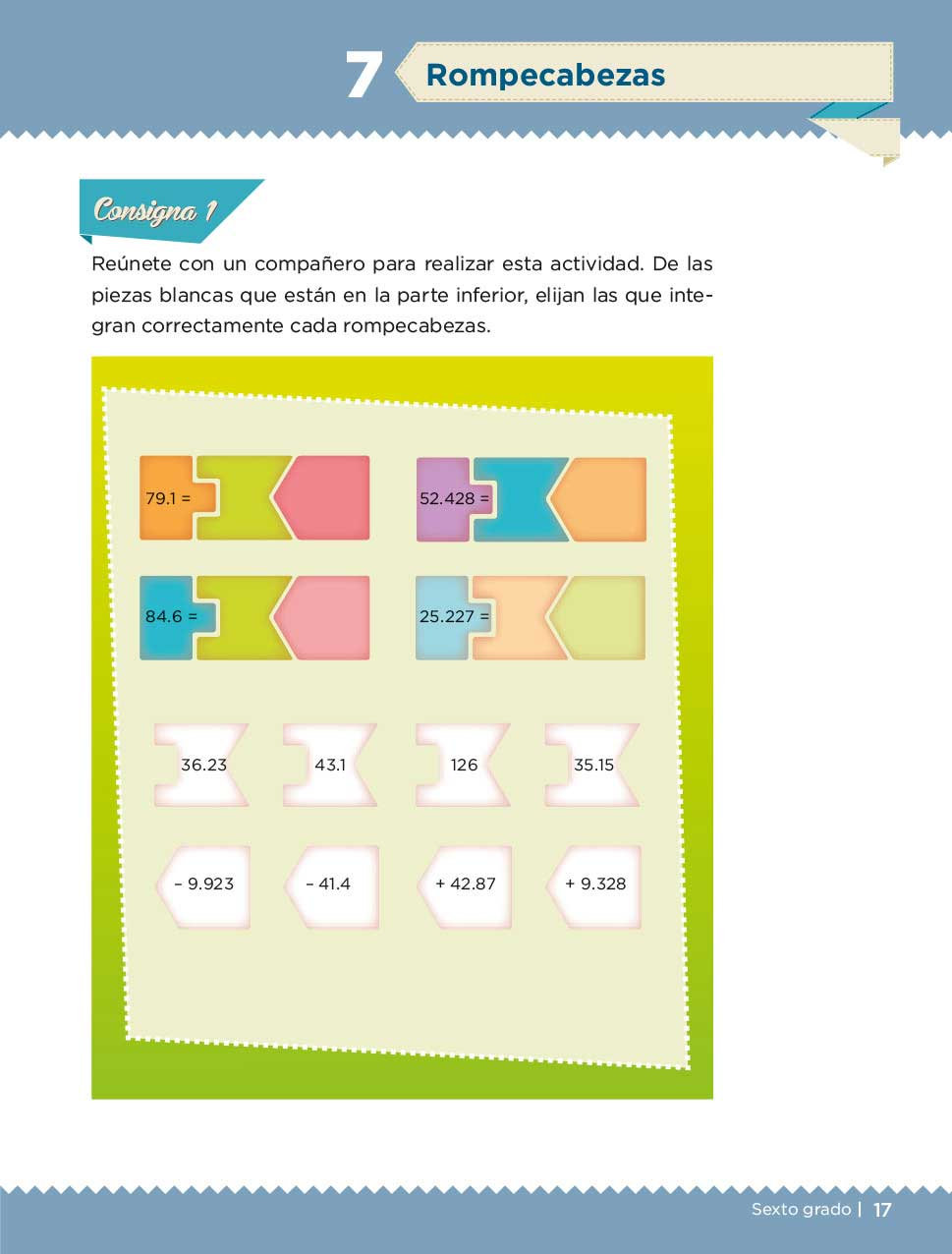
Como en aquella actividad, las piezas que observas te permiten formar sumas y restas de números decimales: a la derecha están los resultados de las operaciones y debajo están los números que nos pueden servir para llegar a esos resultados. Las figuras de las piezas en que se encuentran los números, nos dan una pista de la posición que pueden ocupar en las operaciones, pero cada pieza sólo cabe en un solo espacio de una sola operación.
La solución de este problema, como la de muchos en Matemáticas, requiere de imaginación y creatividad para pensar en las combinaciones posibles que pueden conducir a un resultado, y para prestar atención a las pistas que nos pueden acercar.
Al realizar las operaciones debes poner énfasis en alinear las cifras que tienen el mismo valor posicional, ubicando con claridad dónde debe quedar el punto decimal, y en la escritura de ceros a la derecha del punto para hacer fácilmente comparables los números que se están sumando o restando.
Por último resaltamos dos ideas:
-
La primera, es que, al sumar y restar fracciones y decimales, siempre nos resulta importante poner juntos elementos que sean de la misma clase: peras con peras y manzanas con manzanas. Por esto, en la suma de fracciones buscamos denominadores comunes para estar sumando pedacitos del entero que sean del mismo tamaño. De la misma forma, con los decimales, debemos tener mucho cuidado alineando las cifras de los números que estamos sumando y restando, de manera que las unidades, los décimos, los centésimos, los milésimos, etcétera, queden justamente unos debajo de otros. Para no perdernos, debemos cuidar donde queda el punto decimal y podemos agregar los ceros que nos hagan falta a su derecha para que los números nos sean fácilmente comparables.
-
La segunda es que antes de todo esto, debemos analizar el problema que se nos plantea para definir cuál es la operación que debemos realizar. Tan importante, y a veces tan difícil, como hacer bien las sumas y las restas es definir qué debemos sumar a qué o qué debemos restar a qué para resolver el problema. Solamente de esta manera las Matemáticas nos pueden ser útiles en la vida cotidiana.
Si en tu casa hay libros relacionados con el tema, consúltalos. Así podrás saber más. Si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm


Login to join the discussion