El mundo de las 100 partes II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:56Aprendizaje esperado: Cálculo del tanto por ciento de cantidades mediante diversos procedimientos (aplicación de la correspondencia “por cada 100, n”, (aplicación de una fracción común o decimal, uso de 10% como base).
Énfasis: Calcular porcentajes aplicando la correspondencia “por cada 100, n”.
¿Qué vamos a aprender?
Aprenderás a calcular el tanto por ciento de cantidades mediante diversos procedimientos: Aplicación de la correspondencia “por cada 100, n” aplicación de una fracción común o decimal, uso de 10% como base.
Para explorar más sobre el tema, puedes consultar el libro de texto de Desafíos matemáticos de 6º se explica el tema a partir de la página 36.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/36
¿Qué hacemos?
Te presentaremos información y algunas actividades que te ayudarán a calcular porcentajes aplicando la correspondencia “por cada 100, n”
¿Recuerdas lo que hiciste la sesión anterior?
Viste que el tanto por ciento es una parte de un total que se ha dividido en cien partes.
¿Qué pasaba con el billete o los billetes de cien pesos?
Si tenías quinientos pesos como total, entonces, el uno por ciento equivalía a cinco pesos.
Te diste cuenta de que el porcentaje es un tema que usas en varias actividades de la vida diaria, por ejemplo, en el comercio, los descuentos en productos o servicios se definen por medio de porcentajes, así como los intereses que carga el banco por un préstamo.
Hoy seguirás trabajando sobre el porcentaje o tanto por ciento, realizarás un juego para ampliar y consolidar lo aprendido.
Después, abordarás el desafío número 19 de la página 36 de tu libro de Desafíos matemáticos.
¿Sabes lo que significa un recargo del cinco por ciento?
Actividad 1
Juega con un adulto a lo siguiente:
Primero, tú eres la usuaria o el usuario que paga su recibo y debes calcular los recargos, después cambiarás los papeles, con dinero vas a realizar el pago del recibo y otra persona es la cajera.
Para que sepas cuanto te toca pagar presta atención.
Cada una de estas tarjetas es un recibo de agua con diferente monto de lo que debes.
A partir de esta información debes calcular el recargo, primero escoge una tarjeta.
Es un recibo vencido, por el que tienes que pagar $300 pesos de agua. ¡Pues a pagar se ha dicho! Observa: El recibo dice $300 pesos y tienes que pagar el 5% de recargo.
|
Adeudo vencido: $300 pesos |
¿Qué vas a hacer para calcular el recargo?
Primero, debes calcular el cinco por ciento de trescientos pesos y sabrás cuál es el cinco por ciento de cada billete de cien pesos.
|
|
5% de $100.00 = $5.00 |
5% de $300.00 = $15.00 |
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
Ya sabes cuánto vas a pagar, ahora, debes sumar este recargo al monto original de lo que tenías que pagar, que eran 300 pesos.
|
Monto original |
+ |
Recargo del 5% |
= |
Total a pagar |
|
$300.00 |
+ |
$15.00 |
= |
$315.00 |
Escribe en tu cuaderno el monto exacto.
Ahora cambia los papeles, tú serás la cajera o cajero y la otra persona pagará el recibo que viene en la tarjeta azul.
|
Adeudo vencido: $700 pesos |
Para ver el monto a pagar, realiza el mismo procedimiento, utilizando cuadros similares a los anteriores.
Escribe el monto exacto.
|
|
5% de $100.00 = $5.00 |
5% de $700.00 = $35.00 |
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
|
|
|
5% de $100.00 = $5.00 |
|
Monto original |
+ |
Recargo del 5% |
= |
Total a pagar |
|
$700.00 |
+ |
$35.00 |
= |
$735.00 |
¿Pudiste resolver el problema? ahora tú te encargarás de sacar el monto del último recibo: El verde.
|
Adeudo vencido: $500 pesos |
Este recibo es de 500 pesos, ¿De cuánto es el recargo de 5% y cuánto tienes que pagar?
¿Qué pasaría, si no tuvieras los billetes para representar cada total de cien pesos? ¿Cómo lo resolverías?
Es momento de enfrentar el desafió 19 de la página 36. Lee la consigna y el contenido del anuncio.
Una casa de préstamos ofrece dinero cobrando intereses. Lo anuncia así:
Te prestamos desde $100 hasta $50,000. Paga un interés mensual de 4%. Es decir: Por cada $100 paga sólo $4
Calcula el interés mensual a pagar por las siguientes cantidades.
¿Sabes qué es una casa de préstamos?
Es un lugar donde le prestan dinero a la gente, como en los bancos, se tiene que pagar un interés mensual, que es una cantidad extra que te cobran por haberte prestado el dinero, este interés casi siempre está definido como un porcentaje de la cantidad que se debe.
Cada mes le suman el monto del interés al dinero que te prestaron y le restan lo que has ido pagando. Los bancos y las casas de préstamo te facilitan el poder tener una cantidad de dinero de manera inmediata y que puedas ir pagándola poco a poco. Con el cobro de intereses, los bancos obtienen su ganancia, que a veces llega a duplicar el monto que te prestaron.
Actividad 2
Encontrar algunos desafíos nuevos.
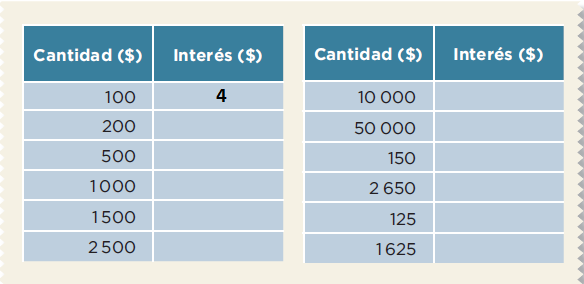
En la primera columna se observan todas las cantidades que representan el dinero que te pueden prestar.
En la segunda columna es el cuatro por ciento de cada una de las cantidades, es decir el dinero que tendría que pagar de interés mensual si se pide un préstamo, considerando cada cantidad que está en la primera columna.
En la segunda columna colocarás la cantidad de dinero que representa el cuatro por ciento de cada total entonces, como el anuncio dice que por cada cien pesos pagan sólo cuatro pesos. La primera respuesta es cuatro pesos.
Si pedimos un préstamo de $200 pesos, ¿Cuánto tienes que pagar? contesta la tabla.
Pasa a la segunda parte de la tabla y podrás observar cantidades más grandes a las que venías trabajando.
Comienza por las más grandes, como diez mil y cincuenta mil, se ve difícil, pero utiliza lo que ya aprendiste y los resultados que ya obtuviste.
También puedes encontrar otras formas de realizar el cálculo y llegar al mismo resultado, por ejemplo:
4% de 1000 = 40
10 x 1000 = 10 000
10 x ( 4% de 1000) = 10 x 40 = 400
Completa la tabla, es importante que revises los procesos realizados. ¡Recuerda que el error es una oportunidad de aprender!

Es posible que hayas seguido distintos caminos para obtener los resultados: Si sumaste unas cantidades u otras; si multiplicaste para avanzar más rápido, lo importante es que revises lo que hiciste para comprobar tus resultados.
Es importante tener claro que el tanto por ciento nos habla de una parte de un total que ha sido dividido en cien partes. Recuerda que cuando hablamos de un porcentaje aplicado a un cargo por pagar después de una fecha indicada o del interés a un préstamo, el porcentaje calculado se suma al total inicial para saber cuánto pagaremos finalmente.
El Reto de Hoy:
Practica sacando el tanto por ciento de una cantidad más chica, ciento cincuenta pesos, ¿Cómo le harías?
Si en tu casa hay libros relacionados con el tema, consúltalos, así podrás saber más. Si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas













Login to join the discussion