Competencia matemática
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:47
Competencia matemática
Aprendizaje esperado: construye y usa una fórmula para calcular el área del triángulo y el trapecio.
Énfasis: deduce la fórmula para calcular el área del triángulo mediante la descomposición de un rectángulo.
¿Qué vamos a aprender?
Aprenderás a deducir la fórmula para calcular el área del triángulo mediante la descomposición de un rectángulo.
¿Qué hacemos?
En la sesión de hoy repasarás algunos de los temas revisados en sesiones pasadas respecto al área de triángulos y trapecios y recordarás la relación que tiene la fórmula para calcular el área de un triángulo mediante la descomposición de un rectángulo.
Vamos a realizar un concurso de matemáticas de lo aprendido en estos días, así que prepárate para ganar puntos.
Aquí las indicaciones para que vayas avanzando:
- Te iré realizando una serie de preguntas.
- Piensa en la respuesta.
- Analiza cómo llegaste al resultado y, si es correcto, obtendrás un punto.
Nuestra competencia será con el desafío número 50 “Divido figuras” que se encuentra en la página 95 de tu libro de Desafíos Matemáticos.
Iniciemos con las preguntas:
¿Cuál es el área de una lámina rectangular que tiene las siguientes medidas 3 metros de largo y 4 metros de ancho?
Respuesta: Son 12 metros cuadrados.
Pon atención para ver si lo resolviste correctamente.
Con la información dada, puedes ver que la lámina tiene forma rectangular, así que, para calcular el área de un rectángulo, debes emplear la fórmula de base por altura, en este caso sería 3 metros de largo por 4 metros de ancho, y nos da 12 metros cuadrados.

La fórmula para calcular el área de un rectángulo es base por altura y recuerda que es importante mencionar que el resultado es en unidades cuadradas porque hablamos de la medida de una superficie.
La siguiente pregunta dice así:
¿Si trazamos una diagonal en un rectángulo obtenemos dos triángulos iguales?
Respuesta: Si, obtendrás dos triángulos iguales.
Te explicaré porque, primero tienes un rectángulo, después traza la diagonal, luego recorta y superpón los rectángulos, y verás que coinciden todos sus lados, es decir, son los mismos.

Sigamos con las preguntas:
¿Los triángulos, son la mitad del área un rectángulo, siempre y cuando tengan la misma altura y base que el rectángulo? tú ¿Qué opinas?
Respuesta: En la figura anterior sólo trazaste una diagonal en el rectángulo para saber que los dos triángulos son iguales y esos triángulos tienen la misma base y la misma altura que el rectángulo, pero como son dos, el área del rectángulo se divide a la mitad.

Espero que hayas contestado correctamente, confío en que, si vas acertando, anota tus resultados.
Pasemos a la siguiente pregunta:
Si el área de un triángulo corresponde a la mitad del rectángulo que tiene la misma base y la misma altura que el triángulo, ¿Cuál es la fórmula para calcular el área del triángulo? ¿Te sabes la respuesta?
Respuesta: Si la fórmula del rectángulo es base por altura y el triángulo es la mitad, es base por altura entre dos.
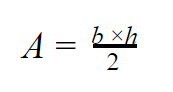
La fórmula para calcular el área de un triángulo es base por altura sobre dos.
Vamos con la siguiente pregunta:
Tenemos un rectángulo de 2 metros de base y 5 metros de altura si trazamos una diagonal, ¿Cuánto mide el área de cada triángulo?
Resultado: Calculando el área del rectángulo, es 2 por 5 lo que da 10 y, al dividir el rectángulo por una diagonal, se forman dos triángulos iguales, por lo tanto, su área queda dividida en 2, así cada triángulo mide 5 metros cuadrados. El área de este triángulo es de 5 metros cuadrados.
La pregunta siguiente, dice así:
Si tenemos un triángulo que mide de base 4 metros y 6 metros de altura. ¿Cuál es el área del rectángulo que tiene las mismas dimensiones?
El resultado es 24 metros cuadrados, ¿Tienes el mismo resultado?
Está pidiendo el área del rectángulo y como tiene las mismas medidas que el triángulo, entonces sólo multiplicas base por altura, y quedaría 4 por 6, igual a 24 metros cuadrados.
Con los datos que tenemos del triángulo, se obtuvo el área del rectángulo.
Tengo más preguntas, pon mucha atención:
Sí el área de un triángulo mide 10 metros cuadrados, ¿Cuánto mide el área del rectángulo cuya base y altura son iguales a las del triángulo?
Resultado: Son 20 metros cuadrados, ¿Qué resultado tienes?
Si el área de un triángulo es la mitad de un rectángulo que tiene la misma base y la misma altura que el triángulo, eso significa que el área del rectángulo es el doble del área del triángulo, por eso multiplicas 2 por 10 son 20 metros cuadrados, que es el área del rectángulo.
La siguiente pregunta dice:
¿Cuál es el área del siguiente triángulo?
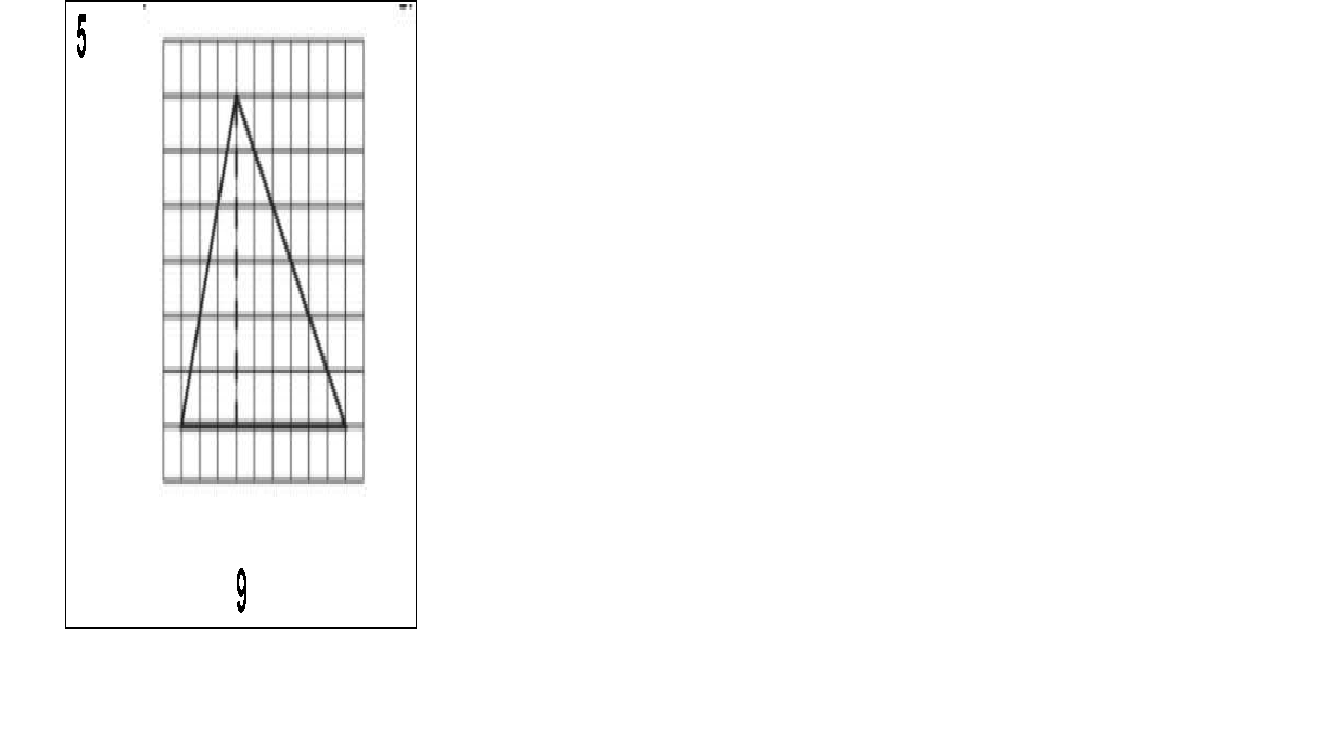
Resultado: Son 27 unidades cuadradas, tiene 9 de base y 6 de altura, primero multiplicas 9 por 6 y son 54, lo divides entre 2, y son 27.
Quiero decirte que si te equivocas no te apures, analiza qué fue lo que no funcionó y corrige. Siempre que hay una equivocación, se asoma una oportunidad de afianzar el conocimiento, pues aprendemos mucho de cuando nos equivocamos.
Las distracciones te pueden generar equivocación, pero si te concentras y las identificas, incluso, te ayudarán a no repetirlas.
Ve el siguiente ejercicio, hay que calcular el área del siguiente triángulo.

El resultado es 33 unidades cuadradas.
Usa la fórmula base por altura entre dos para conocer el área de un triángulo, y entonces multiplica 11 por 6 son 66 entre 2, 33 unidades cuadradas.
Entrando a la recta final, la siguiente pregunta, dice así:
Calcula el área del rectángulo y el área del triángulo marcados en esta imagen.

Resultado: El área del rectángulo es de 32 unidades cuadradas, usa la fórmula de base por altura, que sería 8 por 4, igual a 32 unidades cuadradas.
El área del triángulo, ¿Cuál es?
Resultado: Divide 32 entre 2 y el área del triángulo es igual a 16 unidades cuadradas.
Estoy segura de que has logrado responder correctamente y si fallaste en alguna de las preguntas. No importa eso, lo importante es que reflexiones en qué fallaste y qué necesitas para superar el error.
Con este concurso matemático el día de hoy, recordaste la relación que tiene la fórmula para calcular el área de un triángulo mediante la descomposición de un rectángulo.
Además de poner en práctica lo visto en estas clases te invito para que sigas estudiando, para que estés preparada y preparado para resolver cualquier problema matemático que se te presente.
Diviértete y concéntrate y aunque de pronto te equivoques, ten la seguridad de que estás aprendiendo muchísimo y afianzando el conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/





Login to join the discussion