Descubro los valores de los símbolos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:47
Descubro los valores de los símbolos
Aprendizaje esperado: resuelve problemas que impliquen sumas o restas de fracciones comunes con denominadores diferentes.
Énfasis: resuelve problemas aditivos (con números fraccionarios y con diferentes denominadores), lo que implica recurrir a estrategias como sumar o restar primero la parte entera, o usar fracciones equivalentes para obtener un resultado preestablecido.
¿Qué vamos a aprender?
Aprenderás a resolver problemas que impliquen sumas o restas de fracciones comunes con denominadores diferentes.
¿Qué hacemos?
En la sesión de hoy trabajaras con fracciones. Te pido que estés atenta y atento para descifrar y resolver todo lo que revisaremos y seguro, lograrás aprender algo nuevo.
Para nuestra clase vas a necesitar como primer elemento tu libro de texto de Desafíos Matemáticos, específicamente la página 119 vamos a resolver el Desafío 63 “Una escalera de diez”.
La consigna dice:
“Reúnete con un compañero para identificar cuál de los valores le corresponde a cada símbolo de los que aparecen en la escalera, de tal forma que al sumar los de cada renglón y los de cada columna, el resultado sea 10”
Aquí entra nuestro segundo y tercer elemento que requerimos para esta clase, y son la concentración y tus ganas de seguir aprendiendo.
Lo primero para resolver la consigna es posicionarnos en la fracción: 3 enteros, un medio, porque las flechas indican que ahí empieza la escalera.
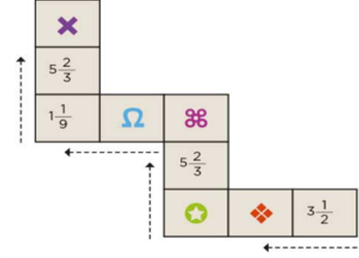
Entonces, Vamos a determinar el valor de estos símbolos, la estrella y el rombo.
Yo creo que así es más difícil, ¿Qué te parece que mejor iniciemos por el otro lado de la escalera? porque en esa columna ya tenemos 2 valores y sólo tenemos un símbolo para descubrir su valor, si comenzamos por el renglón de abajo, entonces tenemos un sólo valor y dos símbolos, creo que eso es más complicado.
Seguramente algunas y algunos consideren empezar a descifrar por abajo, si quieren prueben y al final comparamos nuestros resultados.
Nosotros empezaremos por arriba, ¿Qué piensas que hagamos? Vamos a calcular el valor de la equis.

¿Cómo crees que podríamos hacerlo?
Recuerda que no siempre todos vamos a tener las mismas estrategias para llegar al resultado.
Podemos sumar 5 enteros 2 tercios más un entero un noveno, para saber cuánto valen estos dos cuadros, entonces, para sumar 5 enteros con 2 tercios más 1 entero un noveno, primero separé los enteros de las fracciones para sumarlos por separado. Así que los puse en un paréntesis, 5 más uno son 6 y lo escribí abajo, ahora, tengo que sumar un noveno y dos tercios.
Como las dos fracciones tienen diferente denominador, busqué fracciones equivalentes que tuvieran igual denominador, entonces convertí dos tercios en novenos.
Como ya tengo dos fracciones con igual denominador, la pude sumar y obtuve siete novenos. Finalmente, sume 6 enteros más siete novenos y el resultado es 6 enteros con siete novenos.

Nos falta encontrar el valor de la X, porque aquí solamente sumamos los valores que ya tenemos.
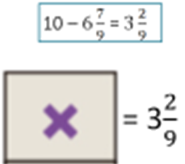
Como el resultado tiene que ser 10 veo cuánto les falta a 6 enteros 7 novenos para llegar a 10 y son 7 novenos más dos novenos son un entero, así que con dos novenos completo un entero más, ya van 7 para 10 son 3 entonces faltan 3 enteros 2 novenos y ese valor es el de X.
Ve anotarlo para ir completando la escalera. Ahora vamos a descubrir los valores de los siguientes símbolos.
Aquí hacen falta 2 valores.
¿Crees que lo podrías resolver de la misma manera que resolviste la columna anterior?
No, porque aquí sólo tenemos un valor y no hay otro valor para sumar, por lo tanto, esta vez, habrá que hacer algo diferente.
¿Tú cómo lo harías? ¿Ya imaginaste algún procedimiento para descubrir estos valores? Espero que sí.
Esta vez vamos a resolverlo con una resta. Diez menos un entero con un noveno, a 10 le quito uno es 9 y a 9 le resto 1 noveno, entonces tenemos ocho enteros con ocho novenos.
Pero ese valor es de los dos símbolos juntos, así que tenemos que pensar cuánto puede valer cada símbolo.
Se me ocurre que probemos con los valores que están en tercios o en novenos, porque el valor que tenemos es en novenos, y se me hace más fácil así, pero ya no considero el valor que ya encontramos.
Entonces voy a probar sumando un entero un noveno más 2 enteros un tercio, y eso nos da 3 enteros 4 novenos, ese valor puede ser de cualquiera de los dos símbolos que están ahí.
Ahora, para saber cuál es el valor de otro símbolo a 10 le resto 3 enteros 4 novenos y eso da como resultado 6 enteros 5 novenos.
Entonces tenemos dos valores que ya encontramos, uno es 2 enteros un tercio y el otro, éste que acabas de encontrar 6 enteros 5 novenos. Ahora sólo falta determinar cuál de los dos le corresponde a cada símbolo de esta fila.
¿Qué podríamos hacer para saber qué valores tiene cada uno?
Si nos fijamos nuevamente en la escalera tenemos aquí un valor que es 5 enteros 2 tercios, entonces para saber con qué valor lo puedo sumar para llegar a 10, tiene que ser 2 enteros 1 tercio, porque si le sumo 6 enteros 5 novenos, ya nos pasamos de 10 así podemos decir que los valores de estos dos símbolos son: 2 enteros un tercio para este símbolo que parece flor, y para el que parece herradura es 6 enteros 5 novenos.
Veamos la siguiente columna.
Esa creo que ya es muy fácil de calcular, porque ya tenemos el valor de la florecita que es 2 enteros con un tercio y el otro cuadro tiene 5 enteros 2 tercios, entonces, esos valores me ayudan a calcular el valor que falta para llegar a 10

Cómo calcularías el valor de la estrella. Esta vez primero voy a sumar 2 enteros un tercio, que es el valor de la florecita más 5 enteros con 2 tercios y el resultado es 8 enteros, ahora resto 10 enteros menos 8 enteros y el resultado es 2 enteros, esto quiere decir que la estrellita vale 2 enteros.
Como todas son fracciones, podríamos buscar una que sea igual a 2 enteros.

Sólo quedan dos valores que no hemos asignado, son 4 enteros 5 décimos y ocho cuartos. Es 8 cuartos, porque 8 entre 4 es igual a 2
Vamos a calcular los valores del último renglón.
Sumamos los tres valores y nos deben dar 10 entonces sumo 8 cuartos más 4 enteros 5 décimos más 3 enteros 1 medio, es igual a 2, porque 8 cuartos es igual a dos enteros, más 4, más 3, y nos dan 9 enteros.
Además 5 décimos es lo mismo que un medio, entonces un medio más un medio es un entero, más los 9 que ya había sumado son 10
Recuerda que en la resolución de problemas podemos llegar al mismo resultado utilizando diferentes caminos y si se equivocaron, no se angustien, revisen qué les falló, para que puedan corregirlo.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion