Nuevos trayectos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46Nuevos trayectos
Aprendizaje esperado: lectura de planos y mapas viales. Interpretación y diseño de trayectorias.
Énfasis: interpretar la información que ofrece un mapa, al identificar y describir la ubicación de algunos lugares de interés. Extraer información de mapas reales y reflexionar sobre las maneras de comunicarla.
¿Qué vamos a aprender?
Interpretarás la información que ofrece un mapa, al identificar y describir la ubicación de algunos lugares de interés.
¿Qué hacemos?
Esta semana realiza un recuento de las sesiones en las que deseamos profundizar, abordando algunos problemas que quedaron pendientes o que complementan lo que ya vimos, y que, dada su relevancia, los retomaremos para que puedas utilizar mejor las herramientas matemáticas.
En esta ocasión recuerda una sesión en la que Ton conoció el mapa donde vivió su papá cuando era niño, nos sirvió para identificar la simbología, y descripción de trayectorias haciendo uso de la Rosa de los vientos. ¿La recuerdas?
Recuerda, los sitios que hay en el pueblo donde vivió el papá de Ton y los trayectos que va a poder realizar después con su familia, también es cierto que tenerlo planeado y definido ayudará mucho a que Ton disfrute ese viaje enormemente.
También es momento de recordar los elementos que vimos en esa sesión, para iniciar te pregunto, ¿Qué significan los dibujos en el mapa?

Es la simbología; sirve para saber si hay parques, hospitales, lugares para comer y muchas otras cosas. Gracias a los símbolos, se pueden representar objetos y condiciones geográficas del lugar; así se determina la ubicación espacial de personas, sitios, rutas, etcétera.
La ubicación espacial en los mapas es para referimos al lugar en el que se encuentra la persona, objeto o sitio al que queremos llegar, para ello utilizamos un símbolo muy importante, la rosa de los vientos; los puntos cardinales de la rosa de los vientos son: norte, sur, este y oeste.
Realicemos un ejemplo, en la siguiente imagen de mi casa, ¿Qué esta al este?
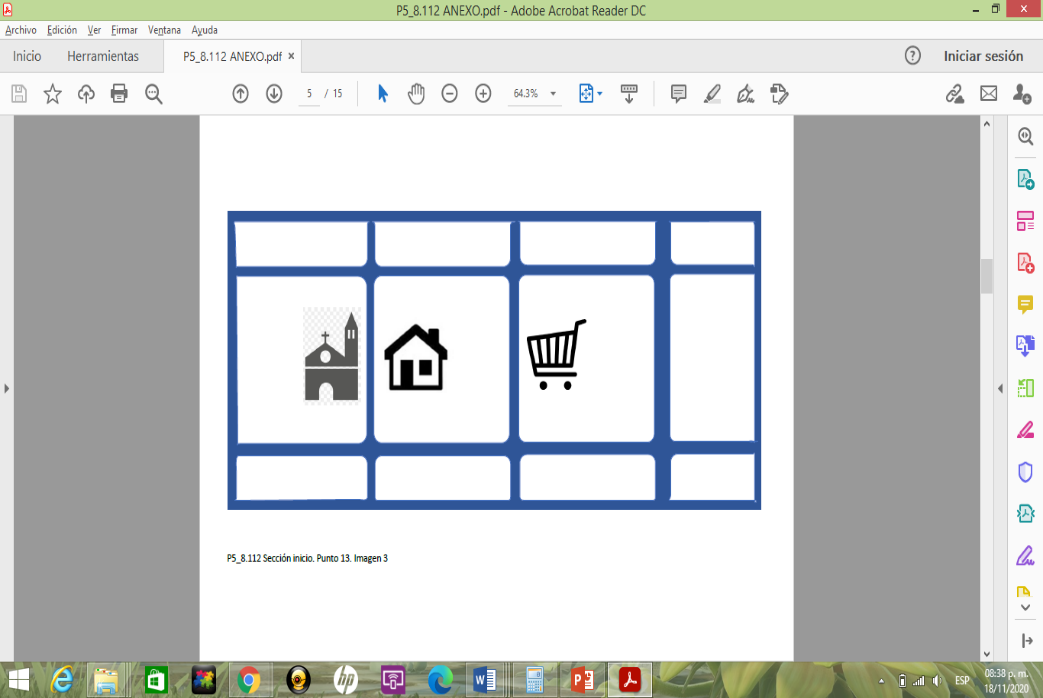
Por la simbología, que es un carrito de supermercado, hay una tienda.
Ahora veamos el mapa, ¿Qué lugares hay en el pueblo donde vivió el papá de Ton?

Hay un hospital, lo identificamos con una H de color rojo.
¿Dónde identificamos un restaurante?
R = Tiene el dibujo de unos cubiertos.
Ese símbolo siempre lo debemos tener presente cada vez que visitamos un lugar, para probar los platillos de la región ya que representa un restaurante.
Vamos muy bien, ahora ubiquemos otros sitios en el mapa, ¿Dónde está la unidad deportiva?
R = Es el espacio grande de color verde.
Ahora empecemos a describir los trayectos que podemos hacer: El primero, de la casa de tus abuelitos hacia la unidad deportiva.
Sería, 1 cuadra hacia el sur, 6 al oeste, así llegarías al centro deportivo.
Hagamos otro recorrido para ir a la iglesia, ¿Qué ruta seguirías?
Avanzaría 5 cuadras al norte y 4 al oeste para llegar al destino.
Ahora te marco la ruta y me dices a donde llegas, irás 1 cuadra al norte, 7 cuadras al oeste, con mucho cuidado, porque son calles transitadas por automóviles y luego avanzas 1 más al norte y llegas a: Un rico restaurante.
Muy bien hemos identificado algunos lugares importantes y trazado rutas del lugar donde viven los abuelitos de Ton, pero, creo que todavía tenemos rutas que describir.
Recuerdas la sesión “Envíos por paquetería”, ayudamos a Emiliano a describir trayectos que su papá hace para entregar mercancía. Ese día, Emiliano nos mandó dos rutas de entrega y sólo pudimos abordar la ruta de un día.
A diferencia de los trayectos que realizaste en el mapa donde viven los abuelitos de Ton que son caminando, aquí son en vehículo.
Además de los elementos que consideramos en el mapa donde viven los abuelitos de Ton, también debemos considerar el sentido vehicular, que es por donde está permitido que los automóviles puedan desplazarse, por eso lo debemos considerar para evitar infracciones o accidentes, así como los señalamientos viales.
Vamos a realizar el trayecto que nos envió Emiliano para las entregas.
El papá de Emiliano se encuentra en la estación metro Polanco, va a realizar cuatro entregas:
- Primera entrega en la cafetería que está en Av. Moliere.
- Segunda entrega en el restaurante.
- Tercera entrega, en una refaccionaria.
- Cuarta entrega en la farmacia.
Están señalados con símbolos, en el siguiente mapa.
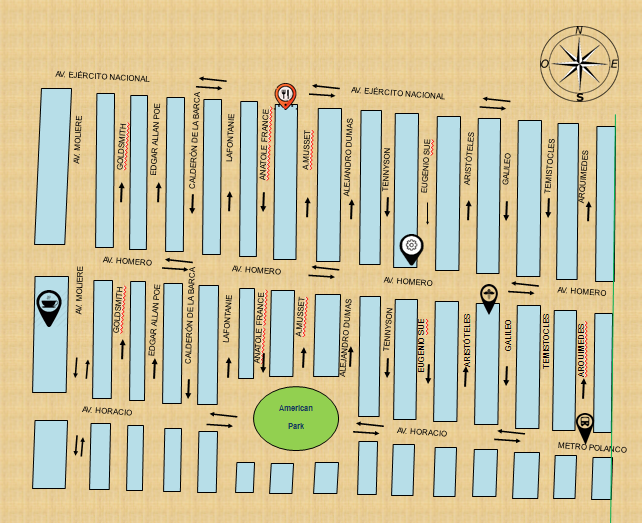
La ruta más corta de acuerdo al sentido vehicular para las entregas es la siguiente: Se va por Av. Horacio en dirección al oeste hacia American Park hasta Av. Moliere, gira a la derecha y avanza media cuadra para hacer entrega del primer paquete, en la cafetería.
Después sigue avanzando por Av. Moliere, es decir, hacia el norte, hasta Av. Ejército Nacional y gira a la derecha; luego avanza cinco cuadras y media para entregar el segundo paquete en el restaurante.
Después avanza sobre la misma calle y, en el mismo sentido, otras tres y media cuadras, luego gira a la derecha en Eugenio Sue y avanza una cuadra para entregar en la refaccionaria.
Ya por último se dirige hacia el este sobre Av. Homero avanza cuadra y media, casi dos y hace la entrega en la farmacia.
El día de hoy, recordamos la sesión en la que mapeamos el pueblo en donde vivió el papá de Ton y retomamos elementos para interpretar la información que nos ofrece un mapa, al identificar y describir la ubicación de algunos lugares de interés, así como la simbología que siempre es de gran ayuda.
Y con el trazo de la ruta para el papá de Emiliano, extrajimos información de mapas reales y reflexionamos sobre las maneras de comunicarla.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion