El mapa de Sofía
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46El mapa de Sofía
Aprendizaje esperado: lectura de planos y mapas viales. Interpretación y diseño de trayectorias.
Énfasis: extraer información de mapas reales y reflexionar sobre las maneras de comunicarla.
¿Qué vamos a aprender?
Identificarás en un mapa las calles principales y secundarias, conocerás la simbología de los mapas y los utilizarás como referencia para llegar a algún punto.
¿Qué hacemos?
Ahora vamos a resolver el misterio del mapa de Sofía.

Veamos qué elementos hay en el mapa, como es un mapa real, vamos a identificar la dimensión de las calles, medios de transporte, servicios, la orientación de las calles con los puntos cardinales.
También en algunos casos los mapas marcan el sentido vehicular, es muy importante para las personas que no conocen las zonas, para evitar algún accidente o infracción.
Vamos a observar el mapa de Sofía, decir qué elementos hay y cómo es la dimensión de las calles.
Unas calles son más grandes y otras más cortas, los trazos de calles más anchas son de color amarillo y son avenidas o calles principales y las más delgadas están de color gris, que son las calles más angostas estas son las calles secundarias, ya identificamos las calles principales y las secundarias.
Recuerdas que en la clase pasada comentamos, que la rosa de los vientos se encuentra en todos los mapas.
La rosa de los vientos, sirve para ubicarnos, representa los cuatro puntos cardinales Norte, Sur, Este y Oeste.
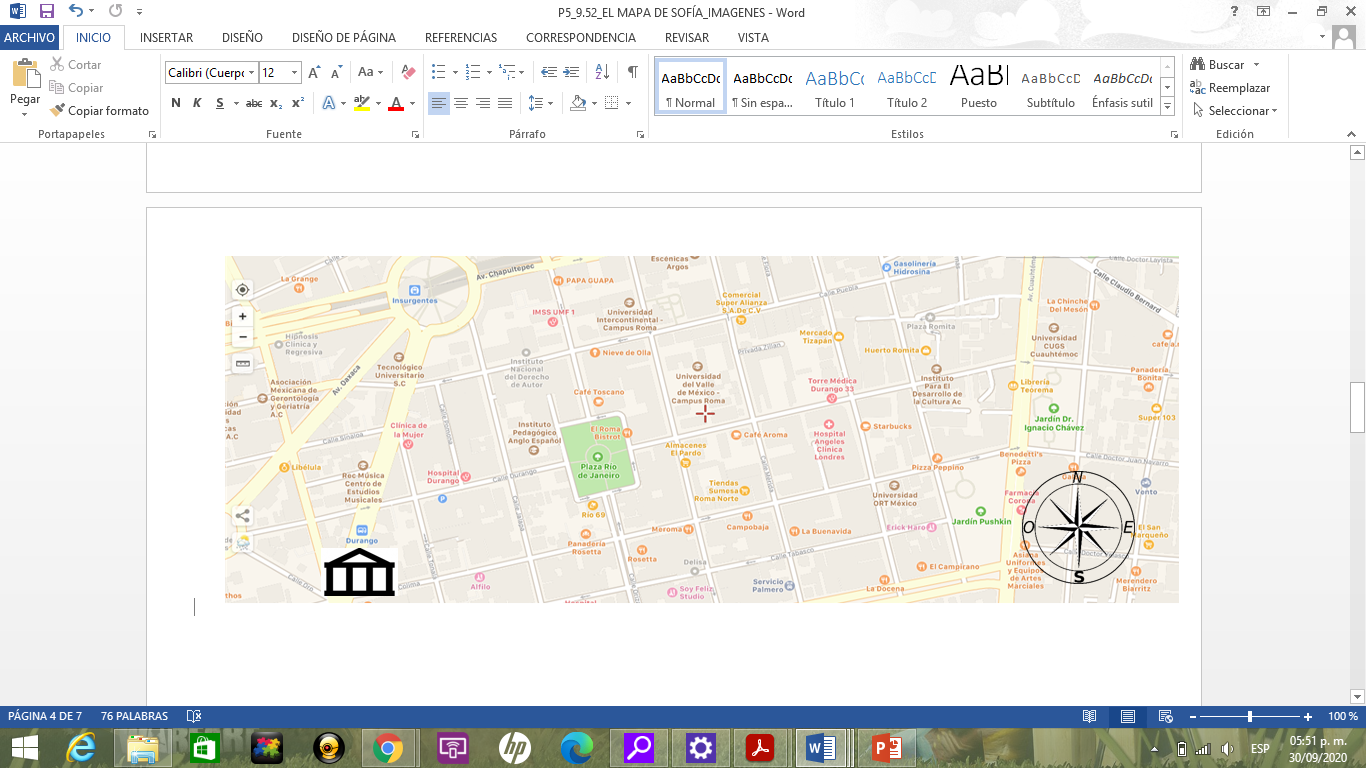
La simbología, sirve para representar sitios y el cuadrado en color verde indica un parque o un lugar con jardines, pasto, árboles, etc.
Se puede identificar la simbología de una cruz, que como ya vimos en la clase pasada es el símbolo de un Hospital.
Los autobuses indican paradas del transporte público y los birretes escuelas, aquí hay una cafetería, porque hay un símbolo de una tácita.
Si quiero ir a comprar despensa, tendría que buscar en el mapa el símbolo que tiene un carrito de supermercado.
Como pudimos ver, encontramos en este mapa simbología de diversos lugares; como camiones, autobuses, arbolitos, una cruz, cubiertos, birretes, tazas, carritos de supermercado; esos símbolos representan un sitio, nos permite usarlos como puntos de referencia.
Ahora que ya viste los elementos del mapa, vamos a describir unos trayectos, yo lo represento en el mapa y tú vas siguiendo la ruta y nos dices a qué lugar llegamos, es importante que lo hagas ¿Estás listo?
Sofía vive en la calle Tabasco esquina con Mérida, ¿Ya lo identificaste?

Observa el mapa si caminas dos cuadras sobre la calle de Mérida hacia el norte y luego una cuadra hacia el este ¿A dónde llegas? a la Torre Médica, Durango 33, independientemente que yo te diga el lugar tú tienes que ubicarlo.
Si sales del Metrobús, en la estación Durango, caminas unos metros hacia el norte hasta llegar a la calle de Durango, sin cruzar la calle, giras al este y caminas tres cuadras en la misma dirección, ¿A dónde llegas? llegas a un lugar muy lindo, que se llama Plaza Río de Janeiro.
Vamos a ubicar un lugar más, si estás en la gasolinera, caminas al sur sobre la calle Morelia tres calles y cruzas la calle, posteriormente das vuelta al este, caminas tres cuadras en esa dirección ¿A dónde llegas? al Restaurante, mira, sin cruzar la calle son cuatro cuadras, cruzando la calle son tres.
Espero que estas actividades le hayan servido a Sofía para identificar algunos elementos del mapa que nos mandó.
El reto de hoy:
Descarga un mapa del lugar donde vives y con tu familia realiza la descripción de diferentes trayectorias.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.






Login to join the discussion