Soy la mitad de...
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46Aprendizaje esperado: localización y trazo de las alturas en diferentes triángulos.
Énfasis: identificar las bases y alturas en triángulos obtenidos al trazar una diagonal en cuadrados, rectángulos, trapecios y paralelogramos.
¿Qué vamos a aprender?
Identificarás las bases y alturas en triángulos obtenidos al trazar una diagonal en cuadrados, rectángulos, trapecios y paralelogramos.
¿Qué hacemos?
Identifica las bases y alturas en triángulos obtenidos al trazar una diagonal en cuadrados, rectángulos, trapecios y paralelogramos.
Seguiremos trabajando con los triángulos, pero esta vez los trazaremos a partir de las siguientes figuras: cuadrado y rectángulo.
Para iniciar nuestra clase, traza en tu cuaderno, un cuadrado de 2 unidades por lado, y un rectángulo de 3 unidades largo y 2 de ancho.
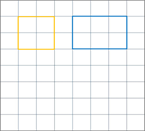
Si tienes hojas de color en casa, traza nuevamente las figuras con las mismas medidas.


Ahora en las figuras de color vamos a trazar una diagonal.


¿Cuántos triángulos se formaron en las figuras?
R = Se forman dos triángulos.
¿Y los triángulos de cada figura tienen las mismas medidas?
R = En las dos figuras los triángulos miden lo mismo.
Ahora ya sabes que tanto en el cuadrado como en el rectángulo al trazar una diagonal formamos dos triángulos iguales.
¿Recuerdas qué es el área de un polígono?
Para recordarlo observa el siguiente video, en el que nos hablarán sobre el área del polígono.
-
Área de un polígono.
https://www.mdt.mx/KrismarApps/index.php/recurso/cargarApp/3070/primaria
Como observaste en el video, el área de una figura es el número que expresa la medida de su superficie, es decir, el espacio que queda encerrado por el perímetro.
Para calcular el área de nuestras figuras, vas a utilizar las que trazaste en las hojas cuadriculadas.
¿Cuál es su área?
R = Del cuadrado son 4 unidades cuadradas y del rectángulo 6 unidades cuadradas.
Si tuviéramos que calcular el área de una figura con 100, 150, 300 o más unidades cuadradas, ¿Cómo le haríamos para calcular, sin contar?
R = Multiplicamos lo que miden por lado. Por ejemplo, en el cuadrado que trazamos, 2 por 2 son los 4 cuadritos. Y en el rectángulo son 3 por 2, son los 6 cuadritos. Recuerda que los cuadritos, son unidades cuadradas.
La fórmula para calcular el área de un cuadrado es: lado por lado y de un rectángulo es: base por altura.
Una figura que tenga como área 100 metros cuadrados, sería un cuadrado de 10 m por 10 m. Para un cuadrado de 10 por 10, su área es de 100 metros cuadrados. Con la información que tenemos sobre las fórmulas para calcular las áreas.
¿Cómo podemos calcular el área de nuestros triángulos que se formaron con el cuadrado y el rectángulo?
R = Sería la mitad de cada figura.
¿Cuánto mide el área?
R = Como es la mitad, los triángulos del cuadrado miden 2 unidades cuadradas y los del rectángulo miden 3 unidades cuadradas.
¿Cómo expresarías la fórmula para calcular el área del triángulo?
R = Área del cuadrado entre 2 y el área del rectángulo entre 2.
El área de los triángulos representa la mitad de estos cuadriláteros, pero la forma correcta de representar la fórmula es la siguiente: Área del triángulo es igual a base por altura y el resultado lo dividimos entre 2.
Razón por la cual, primero trazamos nuestras figuras en la hoja cuadriculada para obtener el área, y después comprender que de un cuadrado o un rectángulo podemos obtener el área del triángulo, ya que éste representa la mitad de un cuadrado o de un rectángulo.
Hoy observamos que de un cuadrado y de un rectángulo, obtenemos, en cada figura, dos triángulos con la misma área, ya que los dos triángulos que formamos en cada figura miden lo mismo.
Anota en tu cuaderno la fórmula para obtener el área de un triángulo, se obtiene multiplicando la base por la altura y dividiendo entre 2.
El día de hoy, con las actividades realizadas logramos deducir la fórmula para calcular el área del triángulo, que es la siguiente: base por altura entre dos; esto porque un triángulo representa la mitad de un cuadrado o de un rectángulo.
Con esa información podrás siempre calcular el área de cualquier triángulo.
El reto de hoy:
Completa los siguientes enunciados:
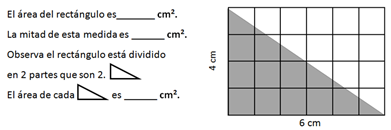
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/primaria.html
Descarga tu clase dando clic aquí


Login to join the discussion