¿Habrá otro?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Aprendizaje esperado: desarrolla y ejercita un algoritmo para dividir números de hasta tres cifras entre un número de una o dos cifras.
Énfasis: establece relaciones entre los procedimientos de la suma, la resta y la multiplicación, y el de la división.
¿Qué vamos a aprender?
Aprenderás a desarrollar el procedimiento que se lleva a cabo para resolver una división. Observarás como la suma, la resta y la multiplicación son algoritmos que te pueden ayudar a dividir una determinada cantidad.
¿Qué hacemos?
Es importante que tengas muy claras las partes que conforman el procedimiento para resolver la división.
Observa la siguiente imagen:

-
Dividendo: Es el número que se debe repartir en partes iguales, es decir, es la cantidad que vamos a dividir, ahí podemos ver que el dividendo es el número 354.
-
Divisor: Es el número de partes iguales entre las cuales se va a fraccionar el dividendo, en este caso el divisor es el número 9.
-
Cociente: Es el número que obtienes al hacer esa división, en la imagen puedes ver que el cociente es el número 39.
-
Residuo: Es la parte que no se pudo distribuir, es lo que sobra, en el ejemplo el residuo es el 3.
Es importante que conozcas que en una división siempre existen dos resultados: el cociente y el residuo, cuando es cero, la división es exacta y no hace falta que lo menciones, pero si tu división no es exacta, es necesario mencionar el residuo como parte de la solución.
En esta operación, 354 se dividió entre 9 y el resultado es 39, y sobraron 3.

¿Qué puedes ver es esta imagen? Unas canicas que están dentro la “casita” que se utiliza en el procedimiento para resolver la división y también hay tres niños.
¿Cuántas canicas son? Son 19 canicas, recuerda que las canicas están en la parte llamada dividendo, es decir es la cantidad que se va a repartir, y los 3 niños serían el divisor, o sea, entre quienes se van a dividir las canicas, con esta información, ¿Qué problema matemático podrías plantear? Puede ser:
-
Tienes 19 canicas y las vas a repartir en partes iguales entre tres amigos, ¿Cuántas canicas le van a tocar a cada uno? ¿Cuál sería el resultado?
Lo que tienes que hacer es una división, 19 entre 3.

Observando el cociente, ya sabes que es lo que le va a corresponder a cada niño, hay 6 canicas y en el residuo puedes observar que queda una canica.
Esta es una representación gráfica que te ayuda a plasmar el proceso de la división. Expresándolo matemáticamente quedaría de la siguiente manera:

Aquí puedes apreciar cada una de las partes de la división.
El siguiente es un ejercicio para que ubiques cada una de esas partes:





Concéntrate y ubica en que flecha va cada nombre de las partes de la división.
Recuerda que el:

Entonces el 19 corresponde al dividendo. ¿Dónde colocarías la tarjeta del divisor?

El número 3 sería el divisor. ¿Cuál es el cociente?

El número 6 es el cociente. Finalmente, ¿Cuál sería el resultado?

Lo que sobró y que forma parte del resultado de la división, el 1 es el residuo.
Sin el residuo no podrías dar una respuesta completa a los problemas que se resuelven con una división.
¿Sabías qué, para llevar a cabo el procedimiento de una división, pones en práctica otros conocimientos como la suma, la resta y la multiplicación?
Pon mucha atención al siguiente problema:

Observa que información te dan y que podrías hacer con ella para responder las dos preguntas que hacen. Una forma es, que cuentes de 6 en 6 hasta llegar a 110 o cerca.
Llegarías hasta 108, porque si sumas otros 6 te pasarías de 110 si te diste cuenta, sumaste 18 veces 6 y te sobraron 2
Este es un camino largo, pero resolviste el problema, ahora utiliza la división para ver si obtienes el mismo resultado, sería 110 azulejos entre 6, así podemos saber cuántas filas se formarían.

Ahora podrías usar la siguiente estrategia. Recuerda que estás buscando un número que multiplicado por 6 te de 110 o el número más cercano.
Como uno no te alcanza para repartir enteros entre 6, entonces tomas hasta el once, once entre seis, toca a uno, uno por seis, seis, lo anotas abajo del 11 y se lo restas, así que te da 5 bajas el cero a la altura del 5 y se forma el 50 ahora tienes 50 entre 6 es 8 porque 8 por seis es 48 este número se lo restas al 50 de donde obtienes 2 como dos ya no alcanza para repartir cantidades enteras entre 6 hasta aquí dejas la división, por lo tanto, obtuviste también 18 y te sobraron 2. Con esta información ya puedes contestar las dos preguntas que están en el problema.
Pon mucha atención y si puedes realízalo también en tú cuaderno. Observa con atención la siguiente imagen y analiza que procedimiento se hizo:

Si observas bien, te darás cuenta de que se está multiplicando por 10 el divisor y lo se le está restando al dividendo, y el resultado es 50
6 x 10 = 60, 110 - 60 = 50
Pero el residuo que es el número 50 aún se puede seguir dividiendo entre 6 observa la siguiente imagen:
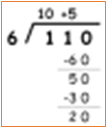
Puedes volver a repartir 50 entre 6 si multiplicas por 5 te dará 30 entonces le puedes sumar 5 al 10 del cociente, pero el 30 de 5 x 6 se lo restas a los 50 que te quedaban y obtienes 20.
5 x 6 = 30, 50 - 30 = 20
El residuo (20) aún se puede repartir entre el divisor, es decir, que todavía se puede hacer 20 entre 6 significa que aún puedes agregar otro número al cociente. Observa la siguiente imagen:

Si observas esta imagen, se agregó el número 3 en el cociente y se multiplicó por el 6 que es el divisor y el resultado que es 18 se restó a 20 quedando 2 como residuo.
3 x 6 = 18, 20 - 18 = 2
El residuo que es 2 ya no se puede dividir entre 6 porque es menor, por lo tanto, así se queda.
Esto te permite ver cómo es que en la división se usan la suma, la resta y la multiplicación. Como lo podrás observar a continuación:

Si sumas 10 + 5 + 3 el resultado es 18. Es decir, 110 entre 6 es igual a 18 y sobrarían 2

Lo que acabas de observar, es la forma en que se puede llegar al resultado de la división mediante la aproximación de cantidades que, al multiplicarse por el divisor, te llevarán al resultado final.
Recuerda que procedimientos o caminos hay muchos, lo más importante es que sepas como se relaciona esta operación con los datos del problema que te hayan planteado. Puedes encontrar un ejemplo similar en la consigna del desafío número 75 de la página 138 de tú libro de texto de Desafíos Matemáticos.

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/138
Lee con atención la consigna:

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/138
Los equipos de Luis, Felipe y Rosa solucionaron el siguiente problema usando los procedimientos que se indican. Coméntenlos y enseguida respondan las preguntas.
Hay 354 losetas para cubrir el piso de un salón de la escuela, después de hacer algunos cálculos, los trabajadores se dieron cuenta de que les conviene acomodarlas en filas de 9 losetas.
¿Cuántas filas podrán colocar? ¿Sobrarán losetas?
Como puedes darte cuenta, es un planteamiento muy parecido al que acabas de ver sobre los azulejos. Ahora observa las tres formas de solución que realizaron los tres equipos:

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/139
Los tres equipos tuvieron la misma respuesta, aunque el procedimiento que siguió cada equipo fue distinto uno del otro.
Si observas la imagen, puedes notar que cada equipo fue aproximando, sumando y restando diversas cantidades del cociente para acercarse al resultado final. Todos obtuvieron como resultado 39 filas de 9 losetas y sobraron 3
Ahora lee las preguntas que se desprenden de los ejemplos que acabas de observar y que están en tú libro de matemáticas:

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/140
¿Qué diferencias observan entre los cálculos que hicieron los equipos de Rosa y de Felipe?
¿Cuál de los tres cálculos consideran que es el más rápido? ¿Por qué?
¿Podrían hacer un cálculo aún más corto que el del equipo de Luis? ¿Por qué?
Responde las preguntas y anota las respuestas.
Recuerda que la suma, la resta y la multiplicación, forman parte del procedimiento para llevar a cabo la resolución de una división.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/primaria.html
Descarga tu clase dando clic aquí




Login to join the discussion