¡Adivina el cuadrilátero!
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Aprendizaje esperado: clasifica cuadriláteros con base en sus características (lados, ángulos, diagonales, ejes de simetría, etcétera).
Énfasis: identifica la característica común de colecciones de cuadriláteros, así como los cuadriláteros que tienen alguna característica en particular.
¿Qué vamos a aprender?
Identificarás la característica común de los cuadriláteros.
¿Qué hacemos?
Iniciarás la sesión con las siguientes preguntas:
-
¿Todos los cuadriláteros tienen dos ejes de simetría?
-
¿Sus cuatro lados tienen la misma medida?
-
¿Qué es un eje de simetría?

Un eje de simetría es: una línea imaginaria que divide una figura en dos partes iguales, es decir, al doblar la figura sobre ese eje todos sus puntos coinciden y se dice que estas dos partes son simétricas con respecto de ese eje. Es como si sobre el eje pusieras un espejo, la imagen que se forma es el complemento de la figura.
Observa las siguientes figuras:



Como puedes observar ambos son cuadriláteros, pero el rombo tiene dos ejes y el trapecio solo uno.
Al doblar en dos partes, sus puntos quedan en espejo, “como si se estuviera reflejando”, por eso se dice que es como si reflejara la imagen, como cuando uno se mira en un espejo.
¿Te diste cuenta de por qué unas figuras tienen ejes de simetría y otras no? Por ejemplo, observa la siguiente figura:

Ten a la mano tu libro de Desafíos Matemáticos en la página 113, el desafío se llama “¿En qué se parecen?”
https://libros.conaliteg.gob.mx/20/P4DMA.htm#page/113
Observa la siguiente imagen que muestra los cuadriláteros de la sesión anterior y analiza que característica en común tienen esos cuadriláteros:
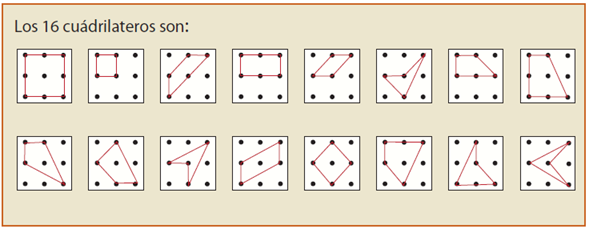
Puedes enumerar cada cuadrilátero e identificar las características que tienen en común.
-
Los cuadriláteros 1, 2 y 13 tienen en común que son cuadrados.
-
En los cuadriláteros 1, 2, 4, 5, 12 y 13, hay dos pares de lados opuestos paralelos.
-
Los cuadriláteros 3, 7 y 8 tienen sólo un par de lados paralelos.
-
Los cuadriláteros 1, 2, 3, 4, 9, 11, 13 y 16, tienen por lo menos un eje de simetría.
-
Los cuadriláteros 6, 11, 15 y 16 tienen un ángulo que es mayor que 180°.
-
Los cuadriláteros 9, 10 y 14, no tienen lados paralelos.
Varios cuadriláteros más no tienen lados paralelos, analízalos e identifica que otros tampoco tienen lados paralelos.
Puedes jugar con tu familia el siguiente juego que se llama: “Adivina la figura”, utilizando imágenes de figuras geométricas y unas tarjetas con características. Pueden formar equipos, pónganse de acuerdo, por turnos cada quien leerá una tarjeta con las características de las figuras. Deberán elegir un color y quien adivine pegará su ficha de color. Pon mucha atención:

-
Tiene 4 ejes de simetría y 2 pares de lados paralelos y con la misma medida. ¿De qué figura estaremos hablando?
La respuesta correcta es: un cuadrado.
-
Cuenta con 1 eje de simetría y tiene un par de lados paralelos.
En la imagen hay 4 figuras con un eje de simetría. Pero, ¿cuál de ellas cumple con la condición de tener un par de lados paralelos? ¿Cuál será la figura correcta?
Si tomas en cuenta la segunda característica que te dan de la figura. entonces la figura es un trapecio.
-
Cuenta con 1 sólo eje de simetría y tiene un ángulo mayor de 180 grados.
Puedes comenzar buscando las figuras que tienen un ángulo mayor de 180°.
-
¿Cuál es la figura geométrica con 1 par de ángulos que mide 90° y con 1 par de lados paralelos?
Es un trapecio rectángulo es la única figura que tiene un par de ángulos de 90°.
-
Tiene exactamente 1 eje de simetría, no tiene lados paralelos y no tiene ángulos mayores que 90 grados.
Es el cometa, ¿recuerdas los papalotes que hiciste la clase pasada? esa figura geométrica se parece a un papalote.
Fíjate bien, este cuadrilátero llamado cometa es un trapezoide con dos lados contiguos de la misma longitud. Aunque esta característica no está en la tarjeta, se puede ver claramente.
-
Tiene exactamente 2 ejes de simetría, dos lados paralelos largos y 2 lados paralelos más cortos.
Es un rectángulo, muy fácil de saber porque la has usado mucho.
Cómo pudiste darte cuenta los cuadriláteros no son tan difíciles de identificar si conoces sus características.
Pon atención y observa la siguiente imagen de los cuadriláteros:

Puedes copiar la imagen anterior en tu cuaderno o en una hoja e ir iluminando con colores diferentes las figuras que vayas observando.
¿Qué figuras puedes observar? Hay rectángulos, podrías iluminarlos con azul.
Por ejemplo, hay un par de rombos, esos los puedes iluminar de color rojo. El romboide, de color amarillo.
También hay un trapecio isósceles, pintaremos de color rosa. La siguiente figura, es un trapecio rectángulo y coloréalo de anaranjado.
Y el cuadrado píntalo de color morado.

En tu cuaderno o en una hoja realiza la siguiente actividad. Consiste en que dibujes un cuadrilátero con las características que se especifican a continuación:
-
Dibuja un cuadrilátero con solo un par de lados paralelos.
-
Dibuja un cuadrilátero con dos pares de lados paralelos.
-
Dibuja un cuadrilátero que tenga solo un eje de simetría.
Esto te servirá para verificar qué tanto aprendiste con estas sesiones sobre cuadriláteros.
Para concluir la sesión de cuadriláteros de hoy, recuerda que:
-
Los cuadriláteros son figuras geométricas formadas por cuatro lados rectos.
-
Sus lados se cortan en puntos llamados vértices y la abertura entre sus lados contiguos se llama ángulo.
-
Algunos cuadriláteros tienen lados paralelos, otros tienen ángulos rectos, otros tienen sus 4 lados diferentes.
Son varias las características que distinguen a unos cuadriláteros de otros.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/primaria.html
Descarga tu clase dando clic aquí



Login to join the discussion