¿Quién llega primero?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27Aprendizaje esperado: resuelve problemas sencillos de suma o resta de fracciones (medios, cuartos, octavos).
Énfasis: realiza sumas y restas sencillas de fracciones con denominadores iguales.
¿Qué vamos a aprender?
Recordarás y practicarás a través de juegos la suma y resta de fracciones.
¿Qué hacemos?
¿ Recuerdas que en sesiones anteriores has trabajado con fracciones?
Recuerdas que has dibujado fracciones, has escrito qué fracción representa la parte sombreada de algunos esquemas y también has encontrado fracciones equivalentes.
¿Recuerdas que también has sumado y restado fracciones? Qué bueno, porque hoy vas a usar la suma y la resta de fracciones para hacer 2 juegos. Esperamos que te gusten los juegos
Antes de jugar, necesitamos que recuerdes algunas cosas sobre la suma y resta de fracciones, para que sea más sencillo y divertido el juego.
Por el momento sólo estás realizando sumas y restas de fracciones con el mismo denominador. Cuando decimos el mismo denominador nos referimos a la cifra que nos indica en cuántas partes dividimos el entero.
Para sumar o restar con igual denominador, lo que debes hacer es conservar el denominador y sólo sumar o restar el numerador, ¿Lo recuerdas?
Por ejemplo, aquí tenemos este material que usaremos para jugar. Las tarjetas azules representan medios. Imagina que tomas 3 tarjetas.
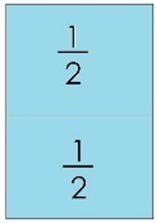
Si las tarjetas representan medios, ¿Qué fracción representa la suma de tus tres tarjetas?
¡Cierto! Representa:
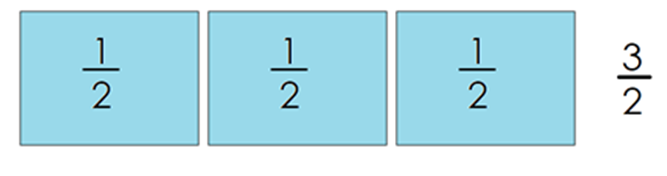
Ahora imagina tomar 4 tarjetas: 1, 2, 3, 4 tarjetas; su suma representa
 y si sumas los tres medios con los 4 medios.
y si sumas los tres medios con los 4 medios.
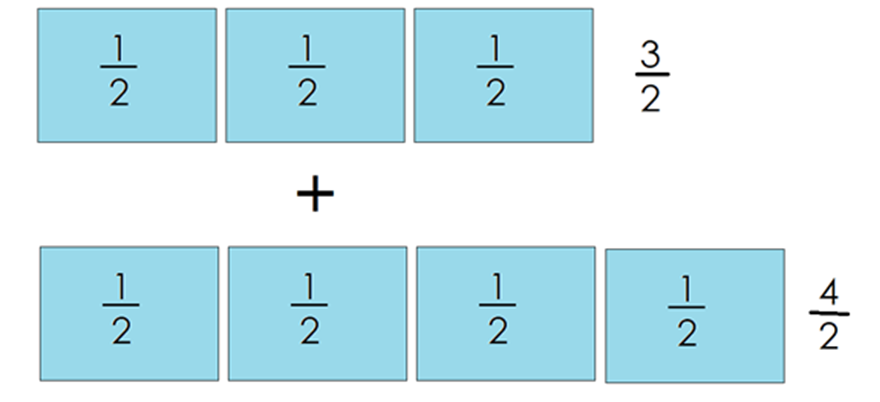
¿Cuánto es?
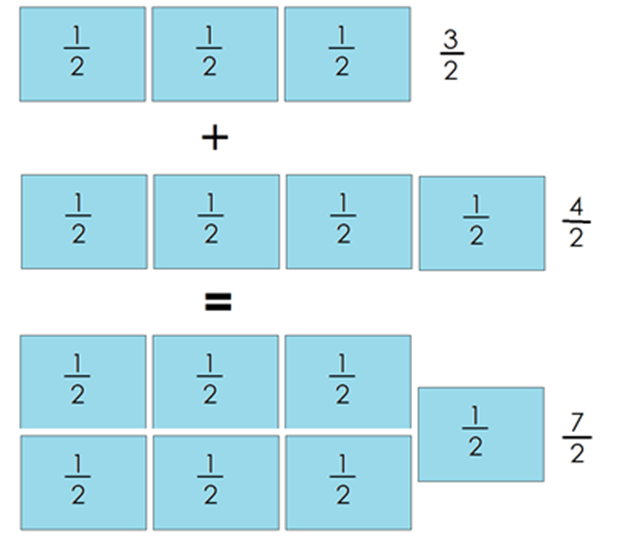
Así es, porque tienes 7 tarjetas o 7 pedazos, y cada uno de ellos representa un medio de enteros iguales, así que se suman los numeradores y el denominador no cambia porque siguen siendo medios, pero también puedes ver que con estos 7 medios puedes formar 3 enteros iguales más un medio, esto es, 3 enteros y medio
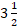
Y para restar es lo mismo; por ejemplo, si a estos siete medios (
 ) que tienes le quieres quitar cinco medios, quedan dos medios (
) que tienes le quieres quitar cinco medios, quedan dos medios (
 ) ¿Está fácil, verdad? Además, esos dos medios equivalen a un entero.
) ¿Está fácil, verdad? Además, esos dos medios equivalen a un entero.
Ahora viene el juego. Te explicamos en qué consiste el juego que se llama, ¿Quién llega primero? Simularemos un juego y si tienes oportunidad de jugarlo con familiares o amigos se van a divertir y aprender mucho.
Necesitas tarjetas como las que se te mostrarán enseguida:
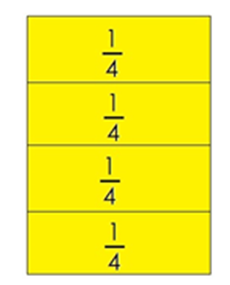
Te damos estas 4 tarjetas, cada una representa un cuarto (
 )
)
El otro jugador también va a tener cuatro tarjetas como las tuyas y sobran algunas, además de las tarjetas, tenemos dos dados: uno que tiene tres caras con el signo más y tres caras con el signo menos y el otro dado tiene dos caras con el número un cuarto, dos caras con el número dos cuartos y dos caras con el número tres cuartos.
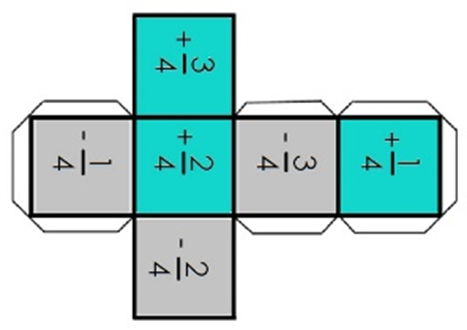
Es diferente este dado, pero así nos va a ser útil. Intercaladamente vamos a lanzar el los dados e ir realizando lo que nos indican.
Esto es: tú tienes tus cuatro cuartos, luego lanzas los dados y digamos que te cae en uno menos y en el otro un cuarto, debes quitar una tarjeta, porque representa un cuarto y, luego le toca al otro jugador. Gana quien después de 7 rondas llegue a 2 enteros, es decir, a ocho cuartos o el que se acerque más sin pasarse.
Tenemos que decirte que, si alguien ya no tiene para restar, pierde su turno, es decir, no realiza nada hasta que le salga algo para sumar y, si se terminan las tarjetas, ahí acaba el juego y contamos para ver quién es el ganador.
Ahora vas a tomar 8 tarjetas de un cuarto (
 ) y va a ganar el primero que se quede sin tarjetas o si llegamos a 10 rondas, ganará quien tenga menos tarjetas. Si se terminan las tarjetas, ahí acaba el juego y contamos para ver quién es el ganador.
) y va a ganar el primero que se quede sin tarjetas o si llegamos a 10 rondas, ganará quien tenga menos tarjetas. Si se terminan las tarjetas, ahí acaba el juego y contamos para ver quién es el ganador.
Con este juego queremos que observes que, tanto la primera vez como la segunda, trabajaste con fracciones de cuartos que pertenecían a enteros del mismo tamaño, y las fracciones también mantuvieron su tamaño, lo único que hacías era agregarlos o quitarlos, pero eso no hizo que dejaran de ser cuartos. Siempre tuvieron el mismo tamaño, lo que cambiaba era la cantidad de pedazos que tenías.
Esta es la razón por la cual en una suma o resta de fracciones, si el denominador es el mismo en todas, no cambia, sólo el numerador se transforma.
Ahora que quedó más claro, vamos a realizar otro juego, pero más difícil.
Ahora tienes aquí estas tarjetas, todas tienen fracciones en octavos y van a tomar 3 tarjetas cada quien.
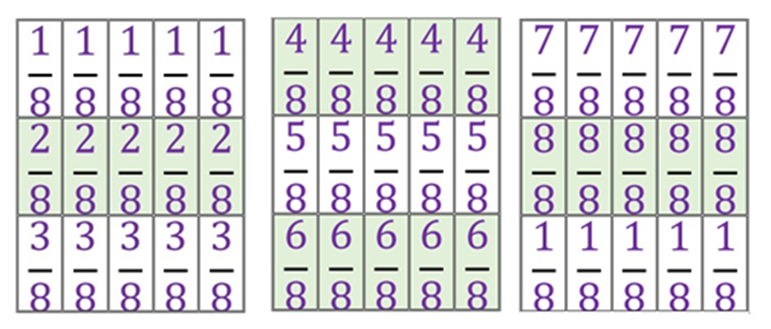
Cada ronda van a voltear sus tarjetas e intentar acercarse lo más que se pueda a diez octavos (
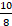 ) no pueden pasarse de esa cantidad. Pueden sumar o restar las tarjetas para llegar a su objetivo, cada ronda gana el que más se acerque.
) no pueden pasarse de esa cantidad. Pueden sumar o restar las tarjetas para llegar a su objetivo, cada ronda gana el que más se acerque.
Ejemplo, comienza. Voy a tomar 3 tarjetas de aquí, ahora imagina que me salió dos octavos, cinco octavos y seis octavos (


 ,) tengo que pensar si las sumo todas o si resto alguna para acercarme lo más que se pueda a diez octavos (
,) tengo que pensar si las sumo todas o si resto alguna para acercarme lo más que se pueda a diez octavos (
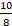 ). Si sumo (:
). Si sumo (:
 +
+
 =
=
 -
-
 =
=
 ) eso quiere decir que me alejo mucho de la meta.
) eso quiere decir que me alejo mucho de la meta.
Toma tus 3 tarjetas que son


 ¿Cuáles sumarías o restarías?
¿Cuáles sumarías o restarías?
Si sumas
 +
+
 =
=
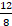 -
-
 =
=
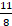 se pasa, entonces debes buscar otra alternativa.
se pasa, entonces debes buscar otra alternativa.
¿Esta?
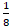 +
+
 =
=
 -
-
 =
=

Bien, como tuve
 y tú
y tú
 esta ronda la habría ganado yo.
esta ronda la habría ganado yo.
Este día ha sido de muchos juegos que te permiten poner en práctica lo que has aprendido.
Recuerdas haber jugado algo similar alguna vez.

https://libros.conaliteg.gob.mx/20/P3DMA.htm ?#page/149
https://libros.conaliteg.gob.mx/20/P3DMA.htm ?#page/173
Hace algunas semanas jugaste con un recortable de tu libro Desafíos Matemáticos que correspondía al desafío 68
Aunque no siempre puedes realizar juegos como éste con lo que aprendes, en ocasiones los juegos nos ayudan a terminar de comprender lo que estamos viendo en las sesiones.
Con el primer juego que realizaste hoy pudiste observar por qué, si el denominador no cambia, sólo sumamos o restamos el numerador.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P3DMA.htm



Login to join the discussion