¡Qué pesados!
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27Aprendizaje esperado: compara, por tanteo, el peso de dos objetos y comprueba en una balanza de platillos.
Énfasis: reflexiona sobre el peso de los objetos en función de su tamaño y del material con el que están hechos.
¿Qué vamos a aprender?
Comprenderás que el peso de los objetos está en función de su tamaño y del material con el que están hechos.
¿Qué hacemos?
Realizarás una actividad que se llama “¡Qué pesados!” vas a trabajar con el peso de algunos objetos. ¿Te preguntarás que eso para que te servirá? Es importante conocer el peso de los objetos pues te da información que puedes utilizar para completar alguna actividad o tarea.
Si alguna vez has acompañado a tu mamá al mercado antes de la pandemia y por supuesto le has ayudado con las bolsas que traía cargando porque a veces pesan mucho, seguro notaste que hay productos que pesan más que otros, por ejemplo, no es lo mismo cargar una bolsa que contenga tres manzanas a una que contenga una sandía.

¿Crees que es muy sencillo identificar qué es lo que pesa más, y que los objetos más grandes siempre son más pesados? Pues te diremos que el peso de un objeto no siempre depende de su tamaño, forma o material.
Te presentamos dos ejemplos.
Imagina que tienes un peluche grande en una mano y en la otra, una cubeta mediana con agua, ¿Cuál crees que pese más?

¿La cubeta con agua? Exacto, aun cuando la cubeta es más pequeña que el peluche. Ahora, te presentamos otro ejemplo.
Imagina que en el patio de tu casa tienes una pelota que es muy grande y la puedes levantar e incluso aventar por los aires sin problema, también tienes unos ladrillos que, aunque son mucho más pequeños te cuesta levantar y aventar, este es otro ejemplo de que no todo lo pequeño es menos pesado.

Estos son ejemplos en los cuales puedes apreciar perfectamente la diferencia de peso que hay entre los objetos.
Ahora, ya estás preparado para comenzar con las actividades del día de hoy, y para eso tenemos una actividad de ordenar.
Te presentamos 6 imágenes de frutas o verduras que tendrás que ordenar de la más pesada a la más liviana.

Se trata de ir colocando en número descendente en las líneas a un lado de las imágenes, es decir, el número 1 a la fruta o verdura más pesada y el número 6 a la fruta o verdura más liviana.
Tomate_______ Manzana_______
Papa _______ Zanahoria_____
Calabaza_____ Plátano_______
¿Terminaste? Excelente, muy bien hecho.
Ahora sí, di, ¿Cuántas respuestas tuviste correctas? ¡Exacto! Es difícil saberlo, ya que las frutas y verduras no pesan siempre lo mismo, así que, ¿Qué te parece si lo comprobamos?
¿Y cómo lo vas a comprobar, si sólo son imágenes las que tienes?
Puedes ir a la cocina y si tienes en casa de las frutas o verduras que están en las imágenes, toma dos piezas, una en cada mano, por ejemplo, la papa y la manzana y siente cuál es la más pesada, puedes hacerlo con las frutas o verduras que tengas y hacer un registro de lo que resulte.
Es muy difícil notar la diferencia cargándolas así con las manos, se parecen mucho y puedes no llegar a percibir las diferencias.
Justamente, en algunas ocasiones es difícil darte cuenta si un objeto, o en este caso, una fruta o verdura, pesa más o menos que otra; generalmente no es así de sencillo comparar el peso.
Lo que se hace en esos casos es hacer uso de una herramienta de precisión, no es una regla ya que la regla te ayuda a medir, pero no pesos sino distancias o longitudes, tampoco es un reloj, ya que el reloj te sirve para medir el tiempo y tú necesitas comparar el peso de los objetos.
Lo que necesitas es algo que ya viste en sesiones anteriores e incluso en la sesión de Ciencias Naturales. ¡Claro! Lo trabajaste hace tiempo y lo que usaste era una balanza

Exactamente, trabajamos con una balanza, y aunque sirve para cosas distintas que una regla o un reloj, sí es una herramienta de medición, como la regla y el reloj. Lo que hace es comparar el peso de dos objetos como frutas, verduras o muchas cosas más, con esto sí puedes comparar cuál fruta o verdura pesa más.
Como te comentamos, una balanza es una herramienta que te permite comparar el peso de dos objetos. Recuerda que el objeto que es más pesado, siempre tiende a bajar y el que es más liviano, siempre sube.
Si en casa tienes una balanza puedes comparar el peso de diferentes objetos y comprobar si está bien el orden que le diste a las frutas y verduras del ejercicio.
¿Cómo te fue, las acomodaste correctamente? ¿Qué te pareció esta actividad? Esta actividad te da una idea más clara de cómo comparar el peso de un objeto con otro.
En caso de que no tengas balanza en tu casa, puedes hacer una con cosas que tengas a la mano.
Quiero que recuerdes que las apariencias engañan y aunque a primera vista parezcan similares, no todas las frutas y verduras pesan lo mismo, generalmente las diferencias de peso cuestan trabajo estimarlas.
¿Te diste cuenta de eso? Hora sí listo para otra actividad.
La siguiente actividad corresponde al desafío 73 de tu libro de matemáticas que se encuentra en la página 159
https://libros.conaliteg.gob.mx/20/P3DMA.htm

https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/159
Esta página te dice: “En equipos, estimen el peso de cada par de objetos y registren en la tabla cuál creen que pesa más, después, comprueben con la balanza si lo que estimaron fue correcto”.
¿Qué te parece si invitas a algún familiar a hacer la actividad contigo? Si no es posible, no te preocupes puedes hacerlo siguiendo las indicaciones del libro.
Seguimos, dice: “Marquen con una paloma si su estimación es correcta”. Necesitas observar primero la tabla.
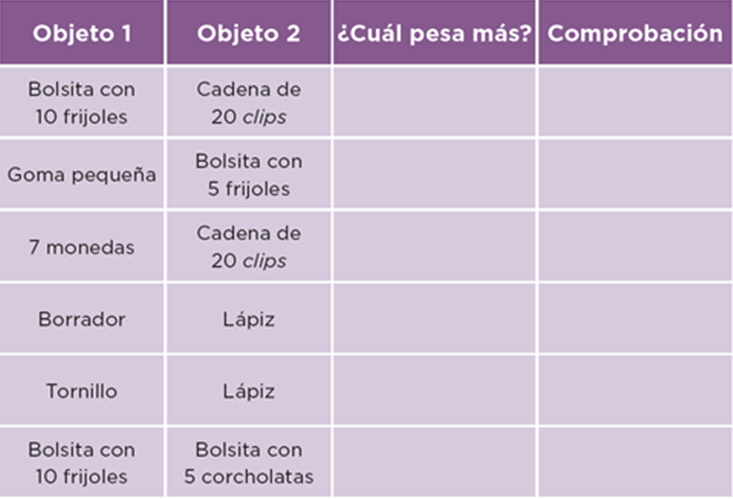
¿Cuáles son los primeros dos objetos a comparar?
Aquí dice que son: una bolsita con 10 frijoles y una cadena de 20 clips. ¿Tú qué opinas? ¿Cuál pesa más?
¿Crees que los 20 clips? Muy bien, vas a anotarlo y cuando acabes de anotar todas tus estimaciones, pasas a comprobarlo con la balanza.
Listo, has terminado, llegó el momento de comprobar tus estimaciones con ayuda de la balanza, colocarás una palomita cuando la estimación fue acertada.
Has terminado con esta actividad, ¿Qué te ha parecido?
Has comprendido que el peso de los objetos está en función de su tamaño y del material con el que están hechos, durante la sesión has comparado objetos como frutas y verduras y también algunos plásticos y metales, también viste que el peso no sólo depende del tamaño o de la forma, que es lo que creías antes.
Un último desafío. ¿Cuántos clips necesito para igualar el peso de un lápiz?
Puedes contestar esa pregunta con ayuda de tu balanza, coloca en un lado de la balanza un lápiz e iguala el peso con clips colocándolos poco a poco en el plato contrario.
Muchas felicidades, ya eres un experto en comparación de pesos.
El reto de hoy:
Esperamos que en casa construyas tu balanza y comiences a descubrir qué pesados son los objetos.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P3DMA.htm



Login to join the discussion