La frutería de Saúl
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27Aprendizaje esperado: identifica escrituras equivalentes (aditivas, mixtas) con fracciones. Comparación de fracciones en casos sencillos (con igual numerador o igual denominador).
Énfasis: establece equivalencias entre números mixtos y sumas de fracciones.
¿Qué vamos a aprender?
Aprenderás a identificar la escritura equivalente de fracciones.
¿Qué hacemos?
En la sesión de hoy me gustaría empezar platicando de la comida y de llevar una sana alimentación, es muy importante comer sano, porque de esa manera fortalecemos nuestro sistema inmunológico y evitamos enfermarnos, además de que ganamos energía, hay que tener presente el plato del buen comer para balancear nuestra alimentación.

Tiene 3 grupos de alimentos: verduras y frutas, cereales y leguminosas y, alimentos de origen animal.

En las fruterías se vende fruta por kilogramo o fracción y jugos por litro o fracción.
Por ejemplo, tomar
1212
litro de jugo de naranja y otros días, un plato de
1414
de kilogramo de papaya.

El jugo de naranja lo tomo 5 veces a la semana y el plato de papaya 7 veces a la semana. Entonces si tomas
1212
litro por día, en dos días tomo 1 litro y en cuatro días, 2 litros, más
1212
del quinto día son 2
1212
litros a la semana.

¿Y cuántos kilogramos de papaya comes a la semana?
Si consumes
1414
de kilogramo al día, sumo
1414
siete veces.
1414 + 1414 + 1414 + 1414 + 1414 + 1414 + 1414 = 7474
Si 4444 es un entero, entonces 7474 = 1 . 3434
El conocer el consumo de sus clientes en litros de jugo y kilogramos de fruta, lo puede ayudar en el manejo los inventarios de la frutería y debe apuntar toda la información de lo que compra y vende.
Ten listo un cuaderno y un lápiz para que nos ayudes a realizar los cálculos necesarios y completar la siguiente
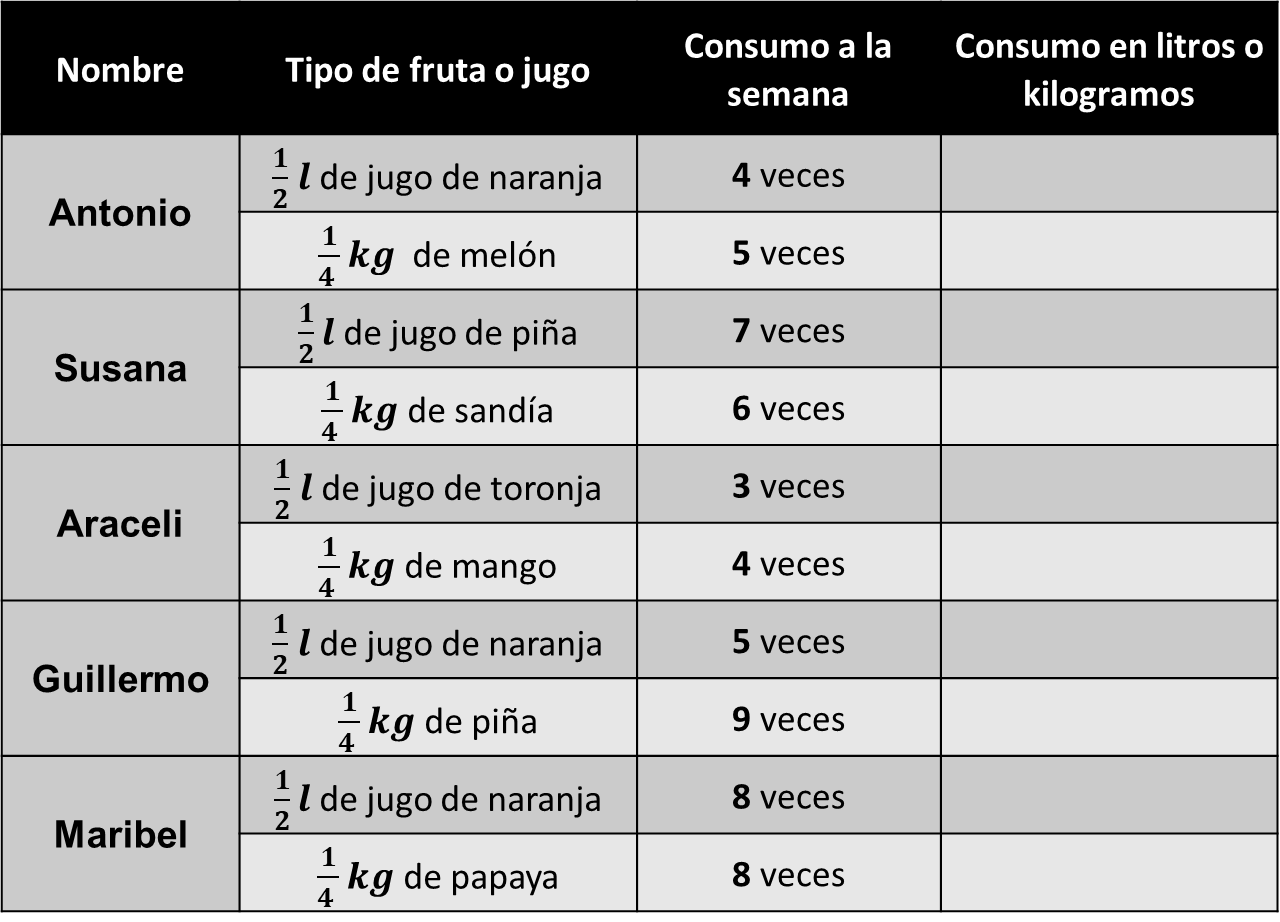
Antonio consume
1212
litro de jugo de naranja 4 veces a la semana. Cada dos días consume un litro y en cuatro días consumirá 2 litros.
También con suma de fracciones:
12 12 + 12 12 +12 12 + 1212 = 4242, cada 2222 es un entero, entonces 4242 = 2 litros de jugo de naranja.
Vayamos rápidamente a su libro de desafíos en la página 108

Es muy parecido maestro, porque en el desafío Luis tenía que tomar
1212
pastilla durante 7 días y para saber cuántas pastillas completas tomó, tenemos que sumar
1212
siete veces:
12 12 + 12 12 + 12 12 + 1212 + 12 12 + 12 12 + 1212 = 7272
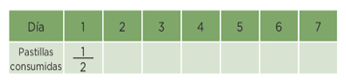
Cada 2 días consume una pastilla completa, en 4 días 2 pastillas, en 6 días 3 pastillas y en el día siete
1212
por lo que en total tomó 3
1212
pastillas.

El consumo de melón de Antonio con los kilogramos come cada día
1414
kg durante cinco días, entonces podemos sumar un cuarto, más un cuarto, más un cuarto, más un cuarto hacen un entero y un cuarto el quinto día. En total come un kilogramo y un cuarto de melón en 5 días, y lo podemos escribir como 1
1414
de kilogramos de melón en 5 días.
También puedes sumar
1414
cinco veces:
[Ecuación] +
1414
+ [Ecuación] +
1414
+ [Ecuación]= [Ecuación], cada
4444
es un entero, entonces
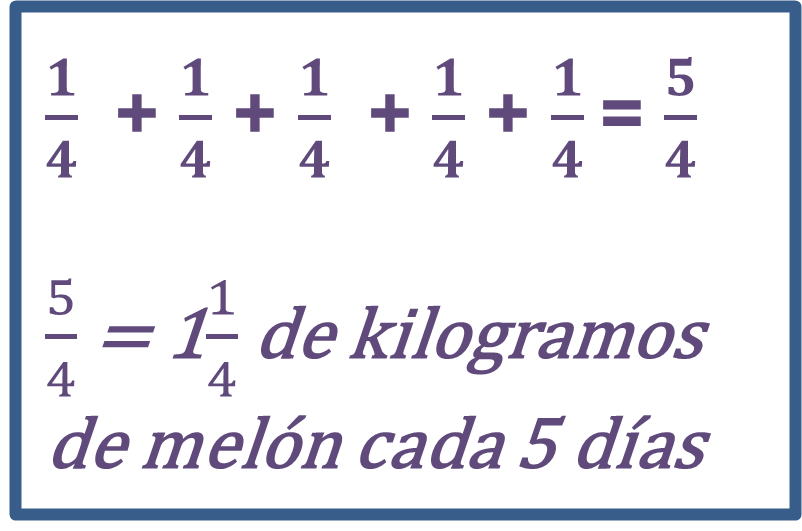

Vamos con Susana, ella consume
1212
litro de jugo de piña, 7 veces a la semana, ¿Cuántos litros de jugo de piña consume a la semana?
Cada 2 días consume un litro, en 6 días consumirá 3 litros y
1212
litro el día 7, son 3
1212
litros de jugo de piña.


Ambos procedimientos nos dan el mismo resultado. Susana consume tres litros y
1212
de jugo de piña a la semana. ¿Qué pasaría si en cada procedimiento nos diera un resultado diferente?
Cuando resolvemos un problema por dos procedimientos diferentes y los resultados son los mismos, es una forma de comprobar que nuestros cálculos fueron correctos, pero si salen diferentes, entonces habrá que revisar dónde estuvo el error.
Vamos con el plato de fruta de Susana, pero vamos a representar la operación que nos permite resolver el problema. Es muy bueno que se puedan hacer cálculos mentalmente, pero también es bueno encontrar la relación entre los datos de un problema y las operaciones que permiten resolverlo.
Ella consume
14
de kilogramo de sandía, 6 veces a la semana, para saber cuánta sandía consume a la semana, podemos recurrir también a una suma que cuyo resultado es
64
kg, que equivale a un kilogramo de sandía más
24
, el resultado es 1
24

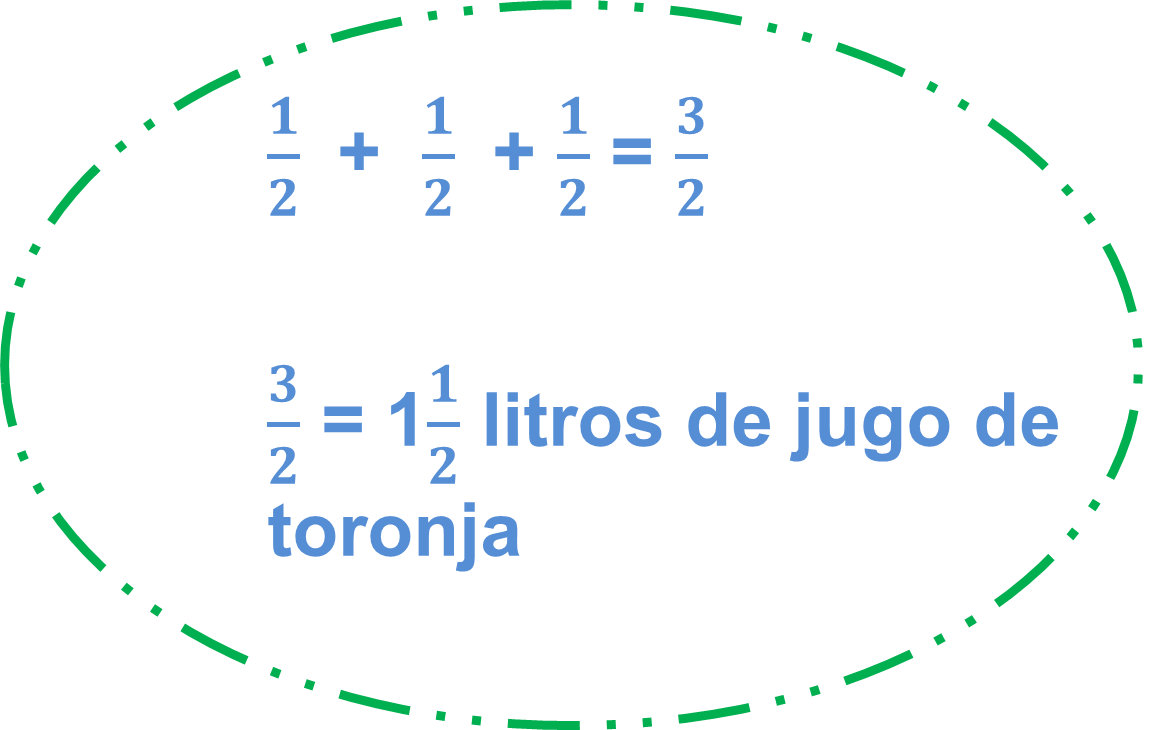
Veamos, cuánto consume a la semana Araceli en total un litro y medio, y aquí dice que toma medio litro cada vez, entonces voy a dividir el litro en medios y ya sabemos que son dos medios, más el otro medio son 3 medios, por lo tanto, Araceli toma medio litro de jugo 3 veces cada semana.
Araceli sólo come un cuarto de kilogramo de mango cada vez y me escribió que en total come dos kilogramos a la semana, entonces divide los dos kilogramos en 4 partes para comer cada vez, por lo tanto, come mango 4 veces a la semana.

Araceli, consume un kilogramo de mango a la semana.
Continuemos con Guillermo, el consume
1212
litro de jugo de naranja 5 veces a la semana, ¿Cuántos litros de jugo de naranja consumirá a la semana?
Como consume
1212
litro al día, en 2 días toma un litro, en 4 días 2 litros y en el quinto día
1212
litro. Consume a la semana 2
1212
litros.


Guillermo consume 2
1212
litros de jugo de naranja a la semana. Vamos ahora con el consumo de fruta de Guillermo, él come
1414
de kilogramo de piña 9 veces a la semana, ¿Cuántos kilogramos de piña comerá a la semana?
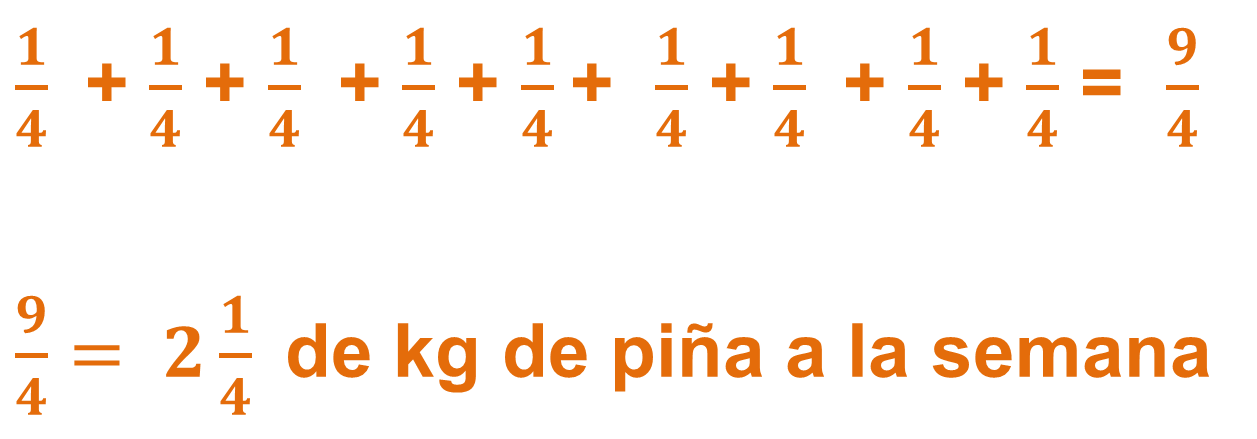
Guillermo consume 2
1414
kilogramos de piña a la semana. Nos toca ahora Maribel, ella toma
1212
litro de jugo de naranja 8 veces a la semana, ¿Cuántos litros de jugo de naranja tomará a la semana?
Seguimos con la cantidad de fruta que consume Maribel, ella come
1414
de kilogramo de papaya 8 veces a la semana, ¿cuánto papaya come en total semanalmente?

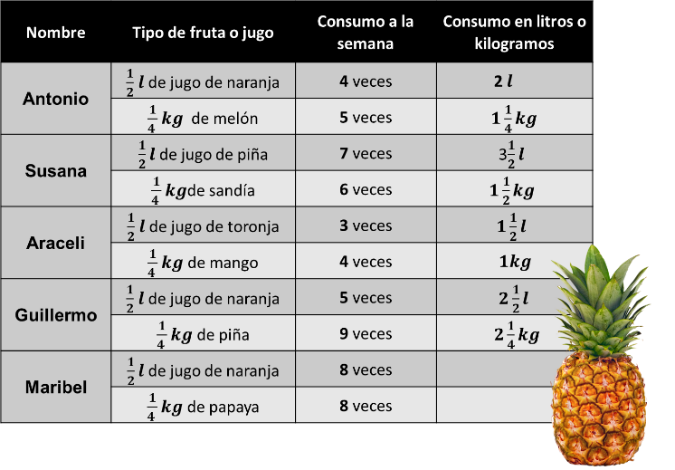
Maribel consume 2 kg de papaya a la semana. Ahora colocaremos los resultados del consumo de litros de jugo y kilogramos de fruta que consumen a la semana unos amigos, ¿Nos ayudas?
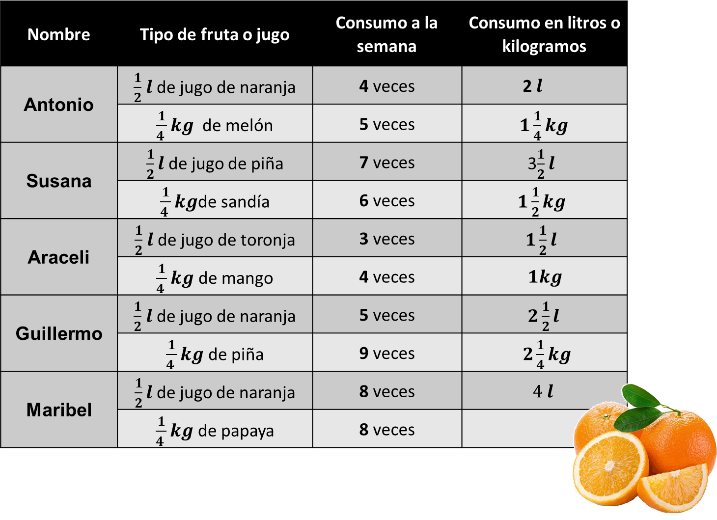


Te invitamos a hacer más ejercicios:
1
2424
ahora tú lo conviertes en una suma de fracciones.
Entonces, como son cuartos, un entero equivale a
4444
y con los
2424
que “sobran” son [Ecuación]
[Ecuación]
2[Ecuación] dos enteros un medio.
[Ecuación] equivalen a un entero, como hay 2 enteros equivalen a [Ecuación] + [Ecuación] = [Ecuación], entonces 2[Ecuación] = [Ecuación]
Multiplica el denominador por los enteros: 2 x 2 = 4 y le sumo el numerador: 4 + 1 = 5 (pasa a escribirlo en el pizarrón), son [Ecuación] entonces 2[Ecuación] = [Ecuación]
Siguiente
5[Ecuación]
[Ecuación] equivale a un entero, [Ecuación] a 2 enteros, [Ecuación] a 3 enteros, [Ecuación] a 4 enteros y [Ecuación] a 5 enteros, más
[Ecuación] que ya no alcanza para otro entero, entonces son [Ecuación], 5[Ecuación] = [Ecuación]
3[Ecuación]
[Ecuación] equivalen a un entero, [Ecuación] a 2 entero y [Ecuación] a 3 enteros, más [Ecuación] son [Ecuación], entonces 3[Ecuación] = [Ecuación]
4[Ecuación]
4[Ecuación] multiplico 2 x 4 = 8 que es el total de medios que corresponden a 4 enteros y le sumo el numerador 1 del [Ecuación] que acompaña a los 4 enteros y obtengo: 8 + 1 = 9 que son los medios convertidos a fracción: 4[Ecuación] = [Ecuación]
5[Ecuación]
5[Ecuación] multiplico 4 x 5 = 20 y le aumento 2, 20 + 2 = 22 y son los cuartos equivalentes: 5[Ecuación] = [Ecuación]
3[Ecuación]
Convierte a octavos, multiplico 8 x 3 = 24 y le aumento 7, 24+7 = 31, son 31 octavos, 3[Ecuación] = [Ecuación]
6[Ecuación]
Multiplica 2 x 6 = 12 y sumo 1, 12+1 = 13, son los medios equivalentes, entonces, 6[Ecuación] = [Ecuación]
Recuerda que en un resultado de suma de fracciones sea igual o mayor el numerador que el denominador, se puede convertir a enteros y se llaman fracciones impropias.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lectura
https://www.conaliteg.sep.gob.mx/primaria.html
Descarga tu clase dando clic aquí



Login to join the discussion